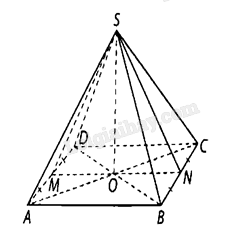
SBT Toán 11 - giải SBT Toán 11 - Kết nối tri thức với cuộc sống

Giải bài 7.53 trang 43 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Cho hình chóp tứ giác đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\)

Đề bài

Cho hình chóp tứ giác đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\), cạnh bên \(SA = \frac{{a\sqrt 5 }}{2}\). Gọi \(SM,SN\) lần lượt là đường cao của tam giác \(SAD\) và tam giác \(SBC\).

a) Chứng minh rằng \(\left( {SMN} \right) \bot \left( {ABCD} \right)\).

b) Tính số đo của góc nhị diện \([S,AD,B]\).

Xác định

c) Tính theo a thể tích khối chóp \(S.ABCD\).

Phương pháp giải - Xem chi tiết

a) Chứng minh rằng \(\left( {SMN} \right) \bot \left( {ABCD} \right)\).

Chứng minh mặt phẳng \(\left( {ABCD} \right)\) chứa \(BC \bot \) \(\left( {SMN} \right).\)

b) Tính số đo của góc nhị diện \([S,AD,B]\).

Xác định được \(\left[ {S,AD,B} \right] = \widehat {SMO}\)
Tính \(\widehat {SMO}\)

c) Tính theo a thể tích khối chóp \(S.ABCD\).

Gọi \(O = AC \cap BD\)
Tính chiều cao \(SO,{S_{ABCD}}\)
Tính thể tích khối chóp \(S.ABCD = \frac{1}{3}SO.{S_{ABCD}}\).

Lời giải chi tiết

a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\).

Ta có: \(AD \bot SM,AD//BC\) nên \(BC \bot SM\), mà \(BC \bot SN\), suy ra \(BC \bot \left( {SMN} \right).\)

Do đó \(\left( {SMN} \right) \bot \left( {ABCD} \right)\).

b) Vì \(MN\) đi qua \(O\) và \(OM \bot AD,SM \bot AD\) nên \(\left[ {S,AD,B} \right] = \widehat {SMO}\), ta tính được\(SM = SN = MN = a\). Do đó tam giác \(SMN\) đều, suy ra \(\widehat {SMN} = {60^ \circ }\).

Vậy \(\left[ {S,AD,B} \right] = {60^ \circ }\).

c) Ta có: \(SO = \frac{{a\sqrt 3 }}{2},{S_{ABCD}} = {a^2}\), suy ra \({V_{S.ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{{{a^3}\sqrt 3 }}{6}\).