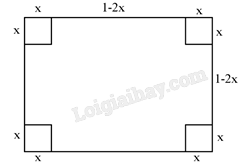
SBT Toán 11 - giải SBT Toán 11 - Kết nối tri thức với cuộc sống

Giải bài 7.40 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Người ta cắt bỏ bốn hình vuông cùng kích thước ở bốn góc của một tấm tôn hình vuông có cạnh \(1{\rm{\;m}}\)

Đề bài

Người ta cắt bỏ bốn hình vuông cùng kích thước ở bốn góc của một tấm tôn hình vuông có cạnh \(1{\rm{\;m}}\) để gò lại thành một chiếc thùng có dạng hình hộp chữ nhật không nắp. Hỏi cạnh của các hình vuông cần bỏ đi có độ dài bằng bao nhiêu để thùng hình hộp nhận được có thể tích lớn nhất?

Phương pháp giải - Xem chi tiết

Áp dụng công thức tính thể tích khối hộp chữ nhật: \({\rm{V}} = a.b.c\).

Trong đó: \(a,b,c\) là độ dài 3 cạnh hình hộp chữ nhật có chung 1 đỉnh

Bước 1: Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều dài cạnh hình vuông nhỏ tại mỗi góc của tấm tôn được cắt bỏ đi (với \(0 < x < \frac{1}{2}\) ).

Tính thể tích hình hộp chữ nhật nhận được

Bước 2: Tìm giá trị lớn nhất của thể tích hình hộp chữ nhật nhận được

Từ đó tìm \(x\)

Lời giải chi tiết

Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều dài cạnh hình vuông nhỏ tại mỗi góc của tấm tôn được cắt bỏ đi (với \(0 < x < \frac{1}{2}\) ).

Thể tích hình hộp chữ nhật nhận được là

\(V = {(1 - 2x)^2} \cdot x = \frac{1}{4} \cdot \left( {1 - 2x} \right) \cdot \left( {1 - 2x} \right) \cdot 4x \le \frac{1}{4} \cdot {\left( {\frac{{1 - 2x + 1 - 2x + 4x}}{3}} \right)^3} = \frac{2}{{27}}\)

Dấu "=" xảy ra khi \(1 - 2x = 4x \Leftrightarrow x = \frac{1}{6}\).

Vậy để thể tích chiếc thùng là lớn nhất thì các cạnh của hình vuông được cắt bỏ đi là \(\frac{1}{6}{\rm{\;m}}\).