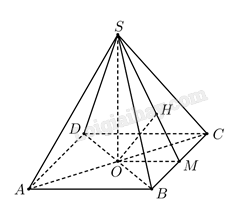
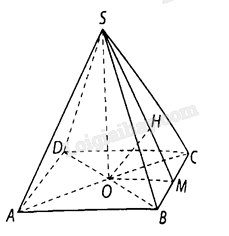
Giải bài 7.37 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Đề bài

Cho hình chóp  có đáy $ABCD$ là hình thoi tâm $O$, biết $SO \bot \left( {ABCD} \right)$, $AC = 2a\sqrt 3 ,BD = 2a$ và khoảng cách từ điểm $A$ đến mặt phẳng $\left( {SBC} \right)$ bằng $\frac{{a\sqrt 3 }}{2}$. Tính theo $a$ thể tích khối chóp $S.ABCD$.

Lời giải chi tiết

Kẻ $OM$ vuông góc với $BC$ tại $M,OH$ vuông góc với $SM$ tại $H$, ta chứng minh được $OH \bot \left( {SBC} \right)$. Vì $O$ là trung điểm của $AC$ nên$d\left( {A,\left( {SBC} \right)} \right) = 2 \cdot d\left( {O,\left( {SBC} \right)} \right) = 2 \cdot OH = \frac{{a\sqrt 3 }}{2}$,

suy ra ${\rm{OH}} = \frac{{{\rm{a}}\sqrt 3 }}{4}$.

Tam giác $OBC$ vuông tại $O$, có $OB = a,OC = a\sqrt 3$

 

và đường cao $OM$ nên $OM = \frac{{OB \cdot OC}}{{BC}} = \frac{{a\sqrt 3 }}{2}$.

Tam giác $SOM$ vuông tại $O$, đường cao $OH$ nên $\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{O{S^2}}}$, suy ra $SO = \frac{a}{2}$.

Vậy ${V_{S \cdot ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{1}{3} \cdot \frac{1}{2} \cdot 2a\sqrt 3  \cdot 2a \cdot \frac{a}{2} = \frac{{{a^3}\sqrt 3 }}{3}$.