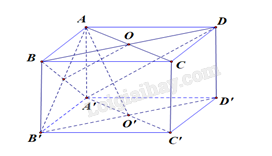
Giải bài 7.27 trang 37 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Đề bài

Cho hình lập phương $ABCD.A'B'C'D'$  có cạnh bằng $a$. Tính theo $a$ khoảng cách

a) Giữa hai đường thẳng  $AB$ và $C'D'$.

b) Giữa đường thẳng $AC$ và $\left( {A'B'C'D'} \right)$.

c) Từ điểm $A$ đường thẳng $B'D'$.

d) Giữa hai đường thẳng  $AC$ và $B'D'$.

Lời giải chi tiết

a) Vì $BC'$ vuông góc với cả hai đường thẳng $AB$và $C'D'$ nên $d\left( {AB,C'D'} \right) = BC' = a\sqrt 2$.

b) Vì $AC\parallel \left( {A'B'C'D'} \right)$ nên $d\left( {AC,\left( {A'B'C'D'} \right)} \right) = d\left( {A,\left( {A'B'C'D'} \right)} \right) = AA' = a$.

c) Gọi $O'$ là giao điểm của $A'C'$ và $B'D'$ ta có $AO' \bot B'D'$, theo định lý Pythagore áp dụng cho tam giác $AA'O'$ vuông tại $A'$ thì $AO' = \frac{{a\sqrt 6 }}{2}$. Do đó, $d\left( {A,B'D'} \right) = AO' = \frac{{a\sqrt 6 }}{2}$.

d) Ta có $d\left( {AC,B'D'} \right) = d\left( {AC,\left( {A'B'C'D'} \right)} \right) = d\left( {A,\left( {A'B'C'D'} \right)} \right) = AA' = a$.