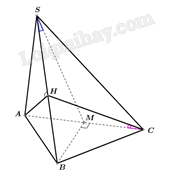
Giải bài 7.15 trang 30 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Đề bài

Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$, đáy là tam giác $ABC$ vuông cân tại $B$, biết $AB = a$, $SA = a\sqrt 6$.

a) Tính tang góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$.

b) Tính sin góc giữa đường thẳng $AC$ và mặt phẳng $\left( {SBC} \right)$.

Quảng cáo

Lời giải chi tiết

a) Gọi $M$ là trung điểm đoạn $AC$ thì $BM \bot AC \Rightarrow BM \bot \left( {SAC} \right) \Rightarrow SM$ là hình chiếu vuông góc của $SB$ lên mặt phẳng $\left( {SAC} \right)$.

Khi đó $\left( {\widehat {SB,\left( {SAC} \right)}} \right) = \left( {\widehat {SB,SM}} \right) = \widehat {BSM}$.

Tam giác $SBM$ vuông tại $M$ có $BM = AM = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}$ và $SM = \sqrt {S{A^2} + A{M^2}}  = \frac{{a\sqrt {26} }}{2}$

Do đó $\tan \widehat {BSM} = \frac{{BM}}{{SM}} = \frac{{\sqrt {13} }}{{13}}$.

b) Trong mp$\left( {SAB} \right)$, kẻ $AH \bot SB$ thì $AH \bot \left( {SBC} \right)$ (vì $AH \bot SB,AH \bot BC$).

Khi đó $HC$ là hình chiếu vuông góc của $AC$ lên mp$\left( {SBC} \right)$.

Suy ra $\left( {\widehat {AC,\left( {SBC} \right)}} \right) = \left( {\widehat {AC,HC}} \right) = \widehat {ACH}$.

Mặt khác tam giác $AHC$ vuông tại $H$ có $AC = a\sqrt 2$ và $AH = \frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{a\sqrt {42} }}{7}$.

Do đó $\sin \widehat {ACH} = \frac{{AH}}{{AC}} = \frac{{\sqrt {21} }}{7}$.