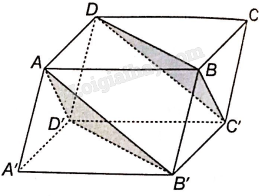
Giải bài 4.36 trang 68 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Đề bài

Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:

a) AB’//C’D’;      

b) Hai mặt phẳng (AB’D’) và (C’B’D) song song với nhau.

Lời giải chi tiết

a) Tứ giác ABCD và BCC’B’ là hình bình hành nên AD//BC, \(AD = BC\) và BC//B’C’ và \(BC = B'C'\), do đó ADC’B’ là hình bình hành nên AB’//C’D.

b) Vì AB’//C’D nên AB’//mp(C’BD)

Chứng minh tương tự ta có: AD’//BC’ nên AD’//mp(C’BD). Mặt phẳng (AB’D’) có hai đường thẳng cắt nhau AB’ và AD’ cùng song song với mp(C’BD) nên hai mặt phẳng (AB’D’) và (C’B’D) song song với nhau.