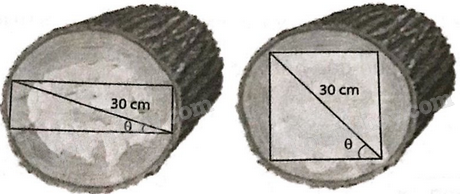
Giải bài 1.64 trang 30 sách bài tập toán 11 - Kết nối tri thức với cuộc sốngMột thanh xà gồ hình chữ hộp chữ nhật được cắt ra từ một khối gỗ hình trụ có đường kính 30cm. Đề bài Một thanh xà gồ hình chữ hộp chữ nhật được cắt ra từ một khối gỗ hình trụ có đường kính 30cm. a) Chứng minh rằng diện tích mặt cắt của thanh xà gồ được tính bởi công thức \(S\left( \theta \right) = 450\sin 2\theta \left( {c{m^2}} \right);\) ở đó góc \(\theta \) được chỉ ra trong hình vẽ dưới đây.
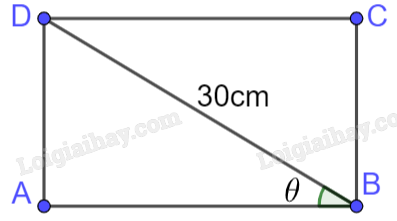
b) Tìm góc \(\theta \) để diện tích mặt cầu của thanh xà gồ lớn nhất. Phương pháp giải - Xem chi tiết + Sử dụng công thức tính diện tích hình chữ nhật: Diện tích hình chữ nhật bằng tích chiều dài và chiều rộng và một số công thức biến đổi lượng giác. + Sử dụng kiến thức: \(\sin x \le 1\) với mọi x. Lời giải chi tiết a) Mặt cắt của thanh xà gồ (hình dưới) là hình chữ nhật có hai kích thước là \(AB = 30\cos \theta \) và \(BC = 30\sin \theta \) Vậy diện tích mặt cắt là: \(S = AB.BC = 30.30.\sin \theta \cos \theta = 450\sin 2\theta \) b) Ta có: \(S = 450\sin 2\theta \le 450\). Vậy diện tích mặt cắt của thanh xà gỗ lớn nhất khi \(\sin 2\theta = 1\) hay \(\theta = {45^0}\)  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
