Trắc nghiệm Các dạng toán về phép nhân, phép chia các số nguyên (tiếp) Toán 6 Cánh diềuĐề bài
Câu 1 :
Giá trị biểu thức \(M = \left( { - 192873} \right).\left( { - 2345} \right).{\left( { - 4} \right)^5}.0\) là
Câu 2 :
Tính giá trị của biểu thức: $A = ax - ay + bx - by$ biết $a + b = - 5;x - y = - 2$
Câu 3 :
Tìm \(x \in Z\) biết \(\left( {x + 1} \right) + \left( {x + 2} \right) + ... + \left( {x + 99} \right) + \left( {x + 100} \right) = 0\).
Câu 4 :
Tập hợp các ước của $ - 8$ là:
Câu 5 :
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
Câu 6 :
Cho \(x \in \mathbb{Z}\) và \(\left( { - 154 + x} \right) \vdots \, 3\) thì:
Câu 7 :
Tìm $n \in Z,$ biết: $\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$
Câu 8 :
Có bao nhiêu số nguyên $a < 5$ biết: $10$ là bội của $\left( {2a + 5} \right)$
Câu 9 :
Cho \(a\) và \(b\) là hai số nguyên khác \(0.\) Biết \(a \, \vdots \, b\) và \(b \, \vdots \, a.\) Khi đó
Câu 10 :
Gọi \(A\) là tập hợp các giá trị $n \in Z$ để \(\left( {{n^2} - 7} \right)\) là bội của \(\left( {n + 3} \right)\). Tổng các phần tử của \(A\) bằng:
Câu 11 :
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
Câu 12 :
Có bao nhiêu số nguyên \(n\) thỏa mãn \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(\left( {n - 1} \right)?\)
Lời giải và đáp án
Câu 1 :
Giá trị biểu thức \(M = \left( { - 192873} \right).\left( { - 2345} \right).{\left( { - 4} \right)^5}.0\) là
Đáp án : C Phương pháp giải :
Áp dụng tính chất nhân một số với \(0\): Số nào nhân với \(0\) cũng bằng \(0\) Lời giải chi tiết :
Vì trong tích có một thừa số bằng \(0\) nên \(M = 0\)
Câu 2 :
Tính giá trị của biểu thức: $A = ax - ay + bx - by$ biết $a + b = - 5;x - y = - 2$
Đáp án : B Phương pháp giải :
Bước 1: Thu gọn biểu thức $A$ về dạng xuất hiện $a + b,x - y$ Lời giải chi tiết :
$A = ax - ay + bx - by$ $ = (ax - ay) + (bx - by)$ $ = a.(x - y) + b.(x - y)$ $ = (a + b).(x - y)$ Thay $a + b = - 5;x - y = - 2$ ta được: \(A = \left( { - 5} \right).\left( { - 2} \right) = 10\)
Câu 3 :
Tìm \(x \in Z\) biết \(\left( {x + 1} \right) + \left( {x + 2} \right) + ... + \left( {x + 99} \right) + \left( {x + 100} \right) = 0\).
Đáp án : B Phương pháp giải :
- Sử dụng quy tắc bỏ ngoặc. - Nhóm \(x\) lại với nhau, nhóm số tự nhiên vào một nhóm. - Áp dụng công thức tổng các số cách đều nhau: Số số hạng = (Số cuối - số đầu):khoảng cách +1 Tổng = (Số cuối + số dầu).số số hạng :2 Lời giải chi tiết :
\(\begin{array}{l}\left( {x + 1} \right) + \left( {x + 2} \right) + ... + \left( {x + 99} \right) + \left( {x + 100} \right) = 0\\(x + x + .... + x) + (1 + 2 + ... + 100) = 0\\100{\rm{x}} + (100 + 1).100:2 = 0\\100{\rm{x}} + 5050 = 0\\100{\rm{x}} = - 5050\\x = - 50,5\end{array}\) Mà \(x\in Z\) nên không có $x$ thỏa mãn.
Câu 4 :
Tập hợp các ước của $ - 8$ là:
Đáp án : A Phương pháp giải :
Sử dụng khái niệm bội và ước của một số nguyên: Nếu $a,b,x \in Z$ và $a = b.x$ thì $a \vdots b$ và $a$ là một bội của $b;b$ là một ước của $a$ Lời giải chi tiết :
Ta có: \( - 8 = - 1.8 = 1.\left( { - 8} \right) = - 2.4 = 2.\left( { - 4} \right)\) Tập hợp các ước của \( - 8\) là: \(A = \left\{ {1; - 1;2; - 2;4; - 4;8; - 8} \right\}\)
Câu 5 :
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
Đáp án : A Phương pháp giải :
+ Bước 1: Tìm ước của \(9\) Lời giải chi tiết :
$a + 4$ là ước của $9$  Vậy giá trị lớn nhất của \(a\) là \(a = 5\)
Câu 6 :
Cho \(x \in \mathbb{Z}\) và \(\left( { - 154 + x} \right) \vdots \, 3\) thì:
Đáp án : A Phương pháp giải :
Sử dụng tính chất chia hết trong tập hợp các số nguyên $a \, \vdots \, m;b \, \vdots \, m \Rightarrow (a + b) \, \vdots \, m$ Lời giải chi tiết :
Ta có: \(\left( { - 154 + x} \right) \, \vdots \, 3\) \(\left( { - 153 - 1 + x} \right) \, \vdots \, 3\) Suy ra \(\left( {x - 1} \right) \, \vdots \, 3\) (do \( - 153 \, \vdots \, 3\)) Do đó \(x - 1 = 3k \Rightarrow x = 3k + 1\) Vậy \(x\) chia cho \(3\) dư \(1.\)
Câu 7 :
Tìm $n \in Z,$ biết: $\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$
Đáp án : B Phương pháp giải :
Bước 1: Phân tích $n + 5$ về dạng $a.\left( {n + 1} \right) + b{\rm{ }}\left( {a,b\; \in \;Z,a \ne 0} \right)$ Lời giải chi tiết :
$\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$$ \Rightarrow \left( {n + 1} \right) + 4 \, \vdots \, \left( {n{\rm{ }} + 1} \right)$ Vì \(n + 1 \, \vdots \, n + 1\) và \(n \in Z\) nên để \(n + 5 \, \vdots \, n + 1\) thì \(4 \, \vdots \, n + 1\) Hay \(n + 1 \in U\left( 4 \right) = \left\{ { \pm 1; \pm 2; \pm 4} \right\}\) Ta có bảng:  Vậy \(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\)
Câu 8 :
Có bao nhiêu số nguyên $a < 5$ biết: $10$ là bội của $\left( {2a + 5} \right)$
Đáp án : A Phương pháp giải :
\(10\) là bội của \(2a + 5\) nghĩa là \(2a + 5\) là ước của \(10\) - Tìm các ước của \(10\) - Lập bảng tìm \(a,\) đối chiếu điều kiện và kết luận. Lời giải chi tiết :
Vì \(10\) là bội của \(2a + 5\) nên \(2a + 5\) là ước của \(10\) \(U\left( {10} \right) = \left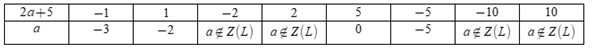\{ { \pm 1; \pm 2; \pm 5; \pm 10} \right\}\) Ta có bảng:  Mà \(a < 5\) nên \(a \in \left\{ { - 3; - 2;0; - 5} \right\}\) Vậy có \(4\) giá trị nguyên của \(a\) thỏa mãn bài toán.
Câu 9 :
Cho \(a\) và \(b\) là hai số nguyên khác \(0.\) Biết \(a \, \vdots \, b\) và \(b \, \vdots \, a.\) Khi đó
Đáp án : D Phương pháp giải :
Sử dụng định nghĩa chia hết: \(a \, \vdots \, b\) nếu và chỉ nếu tồn tại số \(q \in Z\) sao cho \(a = b.q\) Lời giải chi tiết :
Ta có: \(\begin{array}{l}a \, \vdots \, b \Rightarrow a = b.{q_1}\left( {{q_1} \in Z} \right)\\b \, \vdots \, a \Rightarrow b = a.{q_2}\left( {{q_2} \in Z} \right)\end{array}\) Suy ra \(a = b.{q_1} = \left( {a.{q_2}} \right).{q_1} = a.\left( {{q_1}{q_2}} \right)\) Vì \(a \ne 0\) nên \(a = a\left( {{q_1}{q_2}} \right) \Rightarrow 1 = {q_1}{q_2}\) Mà \({q_1},{q_2} \in Z\) nên \({q_1} = {q_2} = 1\) hoặc \({q_1} = {q_2} = - 1\) Do đó \(a = b\) hoặc \(a = - b\)
Câu 10 :
Gọi \(A\) là tập hợp các giá trị $n \in Z$ để \(\left( {{n^2} - 7} \right)\) là bội của \(\left( {n + 3} \right)\). Tổng các phần tử của \(A\) bằng:
Đáp án : A Phương pháp giải :
Biến đổi biểu thức \({n^2} - 7\) về dạng \(a.\left( {n + 3} \right) + b\) với \(b \in Z\) rồi suy ra \(n + 3\) là ước của \(b\) Lời giải chi tiết :
Ta có:\({n^2} - 7 = {n^2} + 3n - 3n - 9 + 2\)\( = n\left( {n + 3} \right) - 3\left( {n + 3} \right) + 2\)\( = \left( {n - 3} \right)\left( {n + 3} \right) + 2\) Vì \(n \in Z\) nên để \({n^2} - 7\) là bội của \(n + 3\) thì \(2\) là bội của \(n + 3\) hay \(n + 3\) là ước của \(2\) \(Ư\left( 2 \right) = \left\{ { \pm 1; \pm 2} \right\}\) nên \(n + 3 \in \left\{ { \pm 1; \pm 2} \right\}\) Ta có bảng:  Vậy \(n \in A = \left\{ { - 5; - 4; - 2; - 1} \right\}\) Do đó tổng các phần tử của \(A\) là \(\left( { - 5} \right) + \left( { - 4} \right) + \left( { - 2} \right) + \left( { - 1} \right) = - 12\)
Câu 11 :
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
Đáp án : C Phương pháp giải :
+ Biến đổi để tách \(5x + 46y\) thành tổng của hai số, trong đó một số chia hết cho $16$ và một số chứa nhân tử \(x + 6y\) + Sử dụng tính chất chia hết trên tập hợp các số nguyên để chứng minh. Lời giải chi tiết :
Ta có: \(\begin{array}{l}5x + 46y = 5x + 30y + 16y\\ = \left( {5x + 30y} \right) + 16y\\ = 5\left( {x + 6y} \right) + 16y\end{array}\) Vì \(5x + 46y\) chia hết cho $16$ và $16y$ chia hết cho $16$ nên suy ra \(5\left( {x + 6y} \right)\) chia hết cho $16.$ Mà $5$ không chia hết cho $16$ nên suy ra \(x + 6y\) chia hết cho $16$ Vậy nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) cũng chia hết cho $16.$
Câu 12 :
Có bao nhiêu số nguyên \(n\) thỏa mãn \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(\left( {n - 1} \right)?\)
Đáp án : C Phương pháp giải :
Áp dụng: \(b\) chia hết cho \(a\) và \(a\) chia hết cho \(b\) thì \(a\),\(b\) là hai số đối nhau (đã chứng minh từ bài tập trước), từ đó suy ra \(n\). Lời giải chi tiết :
Vì \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(n - 1\), Nên \(n - 1\) khác \(0\) và \(n + 5\) khác \(0\) Nên \(n + 5,n - 1\) là hai số đối nhau Do đó: \((n + 5) + (n - 1) = 0\) \(2n + 5 - 1 = 0\) \(2n + 4 = 0\) \(2n = -4\) \(n=-2\) Vậy có 1 số nguyên n thỏa mãn bài toán.
|
