Bài tập trắc nghiệm Toán 6 - Cánh diều

Trắc nghiệm Bài 5: Góc Toán 6 Cánh diều

Làm đề thi

Đề bài

Câu 1 :

Chọn câu sai.

A

Góc là hình gồm hai tia chung gốc
B

Hai tia chung gốc tạo thành góc bẹt
C

Hai góc bằng nhau có số đo bằng nhau
D

Hai góc có số đo bằng nhau thì bằng nhau

Câu 2 :

Chọn câu sai.

A

Góc vuông là góc có số đo bằng $90^\circ$
B

Góc có số đo lớn hơn $0^\circ$ và nhỏ hơn $90^\circ$ là góc nhọn
C

Góc tù là góc có số đo lớn hơn $90^\circ$ và nhỏ hơn $180^\circ$
D

Góc có số đo nhỏ hơn $180^\circ$ là góc tù

Câu 3 :

Chọn phát biểu đúng.

A

Góc có số đo $120^\circ$ là góc vuông
B

Góc có số đo $80^\circ$ là góc tù
C

Góc có số đo $100^\circ$ là góc nhọn
D

Góc có số đo $150^\circ$ là góc tù

Câu 4 :

Cho $9$ tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là

A

$16$
B

$72$
C

$36$
D

$42$

Câu 5 :

Góc trên hình có số đo bao nhiêu độ

A

$50^\circ$
B

$40^\circ$
C

$60^\circ$
D

$130^\circ$

Câu 6 :

Cho hình vẽ sau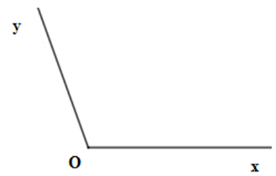

Chọn câu đúng.

A

$\widehat {xOy}$ , đỉnh $O$ , cạnh $Ox$ và $Oy$ .
B

$\widehat {xyO}$ , đỉnh $O$ , cạnh $Ox$ và $Oy$ .
C

$\widehat {Oxy}$ , đỉnh $O$ , cạnh $Ox$ và $Oy$ .
D

$\widehat {xOy}$ , đỉnh $y$ , cạnh $Ox$ và $Oy$ .

Câu 7 :

Kể tên các góc có trên hình vẽ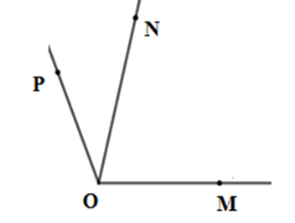

A

$\widehat {MON}$
B

$\widehat {MON};\widehat {NOP};\,\widehat {MOP}$
C

$\widehat {MON};\widehat {NOP}$
D

$\widehat {NOP};\,\widehat {MOP}$

Câu 8 :

Kể tên tất cả các góc có một cạnh là $Om$ có trên hình vẽ sau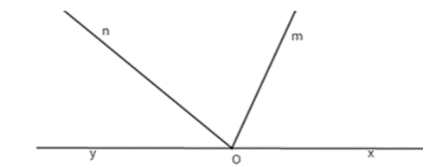

A

$\widehat {xOm};\,\widehat {mOn}$
B

$\,\widehat {mOn}$
C

$\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}$
D

$\widehat {xOm};\,\widehat {mOn};\widehat {mOy}$

Câu 9 :

Cho $\widehat {xOm} = 45^\circ$ và góc $xOm$ bằng góc $yAn$ . Khi đó số đo góc $yAn$ bằng

A

$50^\circ$
B

$40^\circ$
C

$45^\circ$
D

$30^\circ$

Câu 10 :

Cho các góc sau $\widehat A = 30^\circ ;\,\widehat B = 60^\circ ;\,\widehat C = 110^\circ ;\widehat D = 90^\circ$ . Chọn câu sai.

A

$\widehat B < \widehat D$
B

$\widehat C < \widehat D$
C

$\widehat A < \widehat B$
D

$\widehat B < \widehat C$

Câu 11 :

Gọi $O$ là giao điểm của ba đường thẳng $xy;zt;uv$ . Kể tên các góc bẹt đỉnh $O.$

A

$\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}$
B

$\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}$
C

$\widehat {xOy};\,\widehat {uOv}$
D

$\,\widehat {uOv};\,\widehat {zOt}$

Câu 12 :

Cho $n\left( {n \ge 2} \right)$ tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có $28$ góc tạo thành thì $n$ bằng bao nhiêu?

A

$8$
B

$7$
C

$6$
D

$9$

Câu 13 :

Cho trước $4$ tia chung gốc $O.$ Vẽ thêm $3$ tia gốc $O$ không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh $O?$

A

$3$
B

$6$
C

$15$
D

$18$

Câu 14 :

Giả sử có $n\left( {n \ge 2} \right)$ đường thẳng đồng qui tại $O$ thì số góc tạo thành là

A

$2n\left( {n - 1} \right)$
B

$\dfrac{{n\left( {n - 1} \right)}}{2}$
C

$2n\left( {2n - 1} \right)$
D

$n\left( {2n - 1} \right)$

Câu 15 :

Cho góc $xOy$ khác góc bẹt, tia $Oz$ nằm giữa hai tia $Ox;Oy$ . Tia $Ot$ nằm giữa hai tia $Ox;Oz$ . Lấy điểm $A \in Ox;\,B \in Oy$ , đường thẳng $AB$ cắt tia $Oz;Ot$ theo thứ tự tại $M;N$ . Chọn câu sai.

A

Điểm $N$ nằm trong góc $xOz.$
B

Điểm $M$ nằm trong góc $yOt.$
C

Điểm $A$ nằm trong góc $tOz.$
D

Cả A, B đều đúng.

Lời giải và đáp án

Câu 1 :

Chọn câu sai.

A

Góc là hình gồm hai tia chung gốc
B

Hai tia chung gốc tạo thành góc bẹt
C

Hai góc bằng nhau có số đo bằng nhau
D

Hai góc có số đo bằng nhau thì bằng nhau

Đáp án : B

Phương pháp giải :

Sử dụng kiến thức về góc và so sánh hai góc

Để so sánh hai góc ta so sánh số đo của chúng

Lời giải chi tiết :

Ta có:

+ Góc là hình gồm hai tia chung gốc nên A đúng

+ Góc bẹt là góc có hai cạnh là hai tia đối nhau nên B sai vì hai tia chung gốc chưa chắc đã đối nhau

+ Hai góc bằng nhau có số đo bằng nhau nên C đúng

+ Hai góc có số đo bằng nhau thì bằng nhau nên D đúng

Câu 2 :

Chọn câu sai.

A

Góc vuông là góc có số đo bằng $90^\circ$
B

Góc có số đo lớn hơn $0^\circ$ và nhỏ hơn $90^\circ$ là góc nhọn
C

Góc tù là góc có số đo lớn hơn $90^\circ$ và nhỏ hơn $180^\circ$
D

Góc có số đo nhỏ hơn $180^\circ$ là góc tù

Đáp án : D

Lời giải chi tiết :

Ta có góc vuông là góc có số đo bằng $90^\circ$ ; Góc có số đo lớn hơn $0^\circ$ và nhỏ hơn $90^\circ$ là góc nhọn

và góc tù là góc có số đo lớn hơn $90^\circ$ và nhỏ hơn $180^\circ$ nên A, B, C đều đúng.

Góc có số đo nhỏ hơn $180^\circ$ là góc tù là sai vì góc nhọn, góc vuông đều có số đo nhỏ hơn $180^\circ .$

Câu 3 :

Chọn phát biểu đúng.

A

Góc có số đo $120^\circ$ là góc vuông
B

Góc có số đo $80^\circ$ là góc tù
C

Góc có số đo $100^\circ$ là góc nhọn
D

Góc có số đo $150^\circ$ là góc tù

Đáp án : D

Phương pháp giải :

Ta sử dụng các kiến thức:

Góc vuông là góc có số đo bằng $90^\circ$ ;

Góc có số đo lớn hơn $0^\circ$ và nhỏ hơn $90^\circ$ là góc nhọn

Góc tù là góc có số đo lớn hơn $90^\circ$ và nhỏ hơn $180^\circ$

Lời giải chi tiết :

+ Vì $90^\circ < 120^\circ < 180^\circ$ nên góc có số đo $120^\circ$ là góc tù, do đó A sai

+ Vì $0^\circ < 80^\circ < 90^\circ$ nên góc có số đo $80^\circ$ là góc nhọn, do đó B sai

+ Vì $90^\circ < 100^\circ < 180^\circ$ nên góc có số đo $100^\circ$ là góc tù, do đó C sai

+ Vì $90^\circ < 150^\circ < 180^\circ$ nên góc có số đo $150^\circ$ là góc tù, do đó D đúng

Câu 4 :

Cho $9$ tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là

A

$16$
B

$72$
C

$36$
D

$42$

Đáp án : C

Phương pháp giải :

Ta sử dụng kiến thức:

Nếu có $n\,\left( {n \ge 2} \right)$ tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là $\dfrac{{n\left( {n - 1} \right)}}{2}$

Lời giải chi tiết :

Số góc tạo thành là $\dfrac{{9.\left( {9 - 1} \right)}}{2} = 36$ góc.

Câu 5 :

Góc trên hình có số đo bao nhiêu độ

A

$50^\circ$
B

$40^\circ$
C

$60^\circ$
D

$130^\circ$

Đáp án : A

Phương pháp giải :

Quan sát số chỉ giá trị ở vòng trong thước đo độ

Lời giải chi tiết :

Góc trên hình có số đo $50^\circ .$

Chú ý

Một số em đo góc trên theo số đo vòng ngoài nên ra đáp án D sai.

Câu 6 :

Cho hình vẽ sau

Chọn câu đúng.

A

$\widehat {xOy}$ , đỉnh $O$ , cạnh $Ox$ và $Oy$ .
B

$\widehat {xyO}$ , đỉnh $O$ , cạnh $Ox$ và $Oy$ .
C

$\widehat {Oxy}$ , đỉnh $O$ , cạnh $Ox$ và $Oy$ .
D

$\widehat {xOy}$ , đỉnh $y$ , cạnh $Ox$ và $Oy$ .

Đáp án : A

Phương pháp giải :

Áp dụng cách đọc góc, phân biệt được đỉnh và cạnh của góc.

Lời giải chi tiết :

Góc trên hình là góc $\widehat {xOy}$ , đỉnh $O$ , cạnh $Ox$ và $Oy$ .

Câu 7 :

Kể tên các góc có trên hình vẽ

A

$\widehat {MON}$
B

$\widehat {MON};\widehat {NOP};\,\widehat {MOP}$
C

$\widehat {MON};\widehat {NOP}$
D

$\widehat {NOP};\,\widehat {MOP}$

Đáp án : B

Phương pháp giải :

Quan sát hình vẽ, xác định các tia phân biệt chung gốc $O$ từ đó tìm các góc tạo thành.

Lời giải chi tiết :

Các góc tạo thành là: $\widehat {MON};\widehat {NOP};\,\widehat {MOP}$

Câu 8 :

Kể tên tất cả các góc có một cạnh là $Om$ có trên hình vẽ sau

A

$\widehat {xOm};\,\widehat {mOn}$
B

$\,\widehat {mOn}$
C

$\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}$
D

$\widehat {xOm};\,\widehat {mOn};\widehat {mOy}$

Đáp án : D

Phương pháp giải :

Xác định các tia chung gốc $O$ từ đó xác định các góc có một cạnh là $Om.$

Lời giải chi tiết :

Các góc cần tìm là $\widehat {xOm};\,\widehat {mOn};\widehat {mOy}$ .

Câu 9 :

Cho $\widehat {xOm} = 45^\circ$ và góc $xOm$ bằng góc $yAn$ . Khi đó số đo góc $yAn$ bằng

A

$50^\circ$
B

$40^\circ$
C

$45^\circ$
D

$30^\circ$

Đáp án : C

Phương pháp giải :

Sử dụng: Hai góc bằng nhau có số đo bằng nhau

Lời giải chi tiết :

Vì $\widehat {xOm} = \widehat {yAn}$ mà $\widehat {xOm} = 45^\circ$ nên $\widehat {yAn} = 45^\circ .$

Câu 10 :

Cho các góc sau $\widehat A = 30^\circ ;\,\widehat B = 60^\circ ;\,\widehat C = 110^\circ ;\widehat D = 90^\circ$ . Chọn câu sai.

A

$\widehat B < \widehat D$
B

$\widehat C < \widehat D$
C

$\widehat A < \widehat B$
D

$\widehat B < \widehat C$

Đáp án : B

Phương pháp giải :

Trong hai góc: Góc nào có số đo lớn hơn thì góc đó lớn hơn.

Lời giải chi tiết :

Ta có

+) $60^\circ < 90^\circ$ nên $\widehat B < \widehat D$ suy ra A đúng.

+) $110^\circ > 90^\circ$ nên $\widehat C > \widehat D$ suy ra B sai

+) $30^\circ < 60^\circ$ nên $\widehat A < \widehat B$ suy ra C đúng.

+) $60^\circ < 110^\circ$ nên $\widehat B < \widehat C$ suy ra D đúng.

Câu 11 :

Gọi $O$ là giao điểm của ba đường thẳng $xy;zt;uv$ . Kể tên các góc bẹt đỉnh $O.$

A

$\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}$
B

$\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}$
C

$\widehat {xOy};\,\widehat {uOv}$
D

$\,\widehat {uOv};\,\widehat {zOt}$

Đáp án : B

Phương pháp giải :

Xác định các tia phân biệt đối nhau từ đó kể tên các góc bẹt.

Lời giải chi tiết :

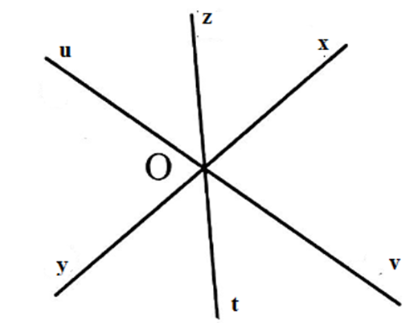Các tia $Ox$ và $Oy;$ $Oz$ và $Ot;Ou$ và $Ov$ là hai tia đối nhau nên các góc bẹt có đỉnh $O$ tạo thành là

$\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}$ .

Câu 12 :

Cho $n\left( {n \ge 2} \right)$ tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có $28$ góc tạo thành thì $n$ bằng bao nhiêu?

A

$8$
B

$7$
C

$6$
D

$9$

Đáp án : A

Phương pháp giải :

Sử dụng:

Nếu có $n\,\left( {n \ge 2} \right)$ tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là $\dfrac{{n\left( {n - 1} \right)}}{2}$

Từ đó tìm ra $n.$

Lời giải chi tiết :

Từ đề bài ta có $\dfrac{{n\left( {n - 1} \right)}}{2} = 28$ nên $n\left( {n - 1} \right) = 56$ mà $56 = 8.7$ , lại có $(n-1)$ và $n$ là hai số tự nhiên liên tiếp nên $n = 8.$

Vậy $n = 8.$

Câu 13 :

Cho trước $4$ tia chung gốc $O.$ Vẽ thêm $3$ tia gốc $O$ không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh $O?$

A

$3$
B

$6$
C

$15$
D

$18$

Đáp án : C

Phương pháp giải :

Ta sử dụng công thức: Nếu có $n\,\left( {n \ge 2} \right)$ tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là $\dfrac{{n\left( {n - 1} \right)}}{2}$

+ Tính số góc ban đầu

+ Tính số góc sau khi thêm

+ Tính số góc tăng thêm

Lời giải chi tiết :

Số góc tạo thành khi có $4$ tia chung gốc là $\dfrac{{4.\left( {4 - 1} \right)}}{2} = 6$ góc

Số góc tạo thành khi có thêm ba tia chung gốc $O$ nữa là $\dfrac{{7.\left( {7 - 1} \right)}}{2} = 21$ góc

Số góc tăng thêm là $21 - 6 = 15$ góc

Chú ý

Một số em tính luôn số góc tạo được từ ba tia chung gốc là sai vì khi thêm ba tia nữa thì tổng số tia là $7$ nên số góc tăng lên sẽ nhiều hơn.

Câu 14 :

Giả sử có $n\left( {n \ge 2} \right)$ đường thẳng đồng qui tại $O$ thì số góc tạo thành là

A

$2n\left( {n - 1} \right)$
B

$\dfrac{{n\left( {n - 1} \right)}}{2}$
C

$2n\left( {2n - 1} \right)$
D

$n\left( {2n - 1} \right)$

Đáp án : D

Phương pháp giải :

+ Xác định số lượng các tia phân biệt chung gốc $O.$

+ Tính góc theo công thức: Nếu có $n\,\left( {n \ge 2} \right)$ tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là $\dfrac{{n\left( {n - 1} \right)}}{2}$

Lời giải chi tiết :

Vì có $n\left( {n \ge 2} \right)$ đường thẳng đồng qui tại $O$ nên số các tia chung gốc tạo thành là $2n$ tia.

Số góc tạo thành là $\dfrac{{2n\left( {2n - 1} \right)}}{2} = n\left( {2n - 1} \right)$ góc.

Câu 15 :

A

Điểm $N$ nằm trong góc $xOz.$
B

Điểm $M$ nằm trong góc $yOt.$
C

Điểm $A$ nằm trong góc $tOz.$
D

Cả A, B đều đúng.

Đáp án : C

Phương pháp giải :

Sử dụng: Khi hai tia $Ox;Oy$ không đối nhau, điểm $M$ là điểm nằm bên trong góc $xOy$ nếu tia $OM$ nằm giữa hai tia $Ox;Oy$ .

Lời giải chi tiết :

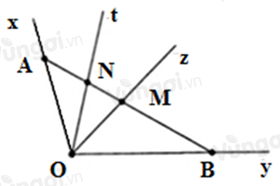Tia $Ot$ nằm giữa hai tia $Ox;Oz$ mà điểm $N$ thuộc tia $Ot$ nên điểm $N$ nằm trong góc $xOz$ . Do đó A đúng.

Tia $Ot$ nằm giữa hai tia $Ox;Oz$ nên điểm $N$ và điểm $A$ nằm cùng phía đối với điểm $M.$

Tia $Oz$ nằm giữa hai tia $Ox;Oy$ nên điểm $A;B$ nằm khác phía đối với điểm $M.$ Suy ra điểm $N$ và điểm $B$ nằm khác phía đối với điểm $M$ , do đó điểm $M$ nằm trong góc $yOt.$ Do đó B đúng, D đúng.

Vì $A \in Ox$ và tia $Ot$ nằm giữa hai tia $Ox;Oz$ nên điểm $A$ không nằm trong góc $tOz.$ Do đó C sai.

Bài liên quan

Trắc nghiệm Bài tập cuối chương VI Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Bài tập cuối chương VI Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 4: Tia Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Bài 4: Tia Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 3: Đoạn thẳng Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Bài 3: Đoạn thẳng Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 2: Hai đường thẳng cắt nhau. Hai đường thẳng song song Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Bài 2: Hai đường thẳng cắt nhau. Hai đường thẳng song song Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 1: Điểm. Đường thẳng Toán 6 Cánh diều

Luyện tập và củng cố kiến thức Bài 1: Điểm. Đường thẳng Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Trắc nghiệm Bài 5: Góc Toán 6 Cánh diều

Trắc nghiệm Bài tập cuối chương VI Toán 6 Cánh diều

Trắc nghiệm Bài 4: Tia Toán 6 Cánh diều

Trắc nghiệm Bài 3: Đoạn thẳng Toán 6 Cánh diều

Trắc nghiệm Bài 2: Hai đường thẳng cắt nhau. Hai đường thẳng song song Toán 6 Cánh diều

Trắc nghiệm Bài 1: Điểm. Đường thẳng Toán 6 Cánh diều