Trắc nghiệm Các dạng toán về phép nhân và phép chia hết hai số nguyên (tiếp) Toán 6 Chân trời sáng tạoĐề bài
Câu 1 :
Chọn câu sai.
Câu 2 :
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left( {x - 7} \right)\left( {x + 5} \right) < 0\)?
Câu 3 :
Tập hợp các ước của $ - 8$ là:
Câu 4 :
Có bao nhiêu ước của \( - 24.\)
Câu 5 :
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
Câu 6 :
Cho \(x \in \mathbb{Z}\) và \(\left( { - 154 + x} \right) \vdots \, 3\) thì:
Câu 7 :
Tìm $n \in Z,$ biết: $\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$
Câu 8 :
Có bao nhiêu số nguyên $a < 5$ biết: $10$ là bội của $\left( {2a + 5} \right)$
Câu 9 :
Tìm $x,$ biết: $x \, \vdots \, 6$ và $24 \, \vdots \, x$
Câu 10 :
Cho \(a\) và \(b\) là hai số nguyên khác \(0.\) Biết \(a \, \vdots \, b\) và \(b \, \vdots \, a.\) Khi đó
Câu 11 :
Gọi \(A\) là tập hợp các giá trị $n \in Z$ để \(\left( {{n^2} - 7} \right)\) là bội của \(\left( {n + 3} \right)\). Tổng các phần tử của \(A\) bằng:
Câu 12 :
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
Câu 13 :
Có bao nhiêu số nguyên \(n\) thỏa mãn \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(\left( {n - 1} \right)?\)
Câu 14 :
Trong các phát biểu sau đây, phát biểu nào đúng?
Lời giải và đáp án
Câu 1 :
Chọn câu sai.
Đáp án : C Phương pháp giải :
- Tính và kiểm tra các đáp án, sử dụng quy tắc nhân hai số nguyên cùng dấu, khác dấu. Lời giải chi tiết :
Đáp án A: \(\left( { - 19} \right).\left( { - 7} \right) > 0\) đúng vì tích hai số nguyên cùng dấu là một số nguyên dương. Đáp án B: \(3.\left( { - 121} \right) < 0\) đúng vì tích hai số nguyên khác dấu là một số nguyên âm. Đáp án C: \(45.\left( { - 11} \right) = - 495 > - 500\) nên C sai. Đáp án D: \(46.\left( { - 11} \right) = - 506 < - 500\) nên D đúng.
Câu 2 :
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left( {x - 7} \right)\left( {x + 5} \right) < 0\)?
Đáp án : B Phương pháp giải :
Sử dụng kiến thức \(A.B < 0\) thì \(A\) và \(B\) trái dấu. Lời giải chi tiết :
\(\left( {x - 7} \right)\left( {x + 5} \right) < 0\) nên \(x - 7\) và \(x + 5\) khác dấu. Mà \(x + 5 > x - 7\) nên \(x + 5 > 0\) và \(x - 7 < 0\) Suy ra \(x > - 5\) và \(x < 7\) Do đó \(x \in \left\{ { - 4, - 3, - 2, - 1,0,1,2,3,4,5,6} \right\}\) Vậy có \(11\) giá trị nguyên của \(x\) thỏa mãn bài toán.
Câu 3 :
Tập hợp các ước của $ - 8$ là:
Đáp án : A Phương pháp giải :
Sử dụng khái niệm bội và ước của một số nguyên: Nếu $a,b,x \in Z$ và $a = b.x$ thì $a \vdots b$ và $a$ là một bội của $b;b$ là một ước của $a$ Lời giải chi tiết :
Ta có: \( - 8 = - 1.8 = 1.\left( { - 8} \right) = - 2.4 = 2.\left( { - 4} \right)\) Tập hợp các ước của \( - 8\) là: \(A = \left\{ {1; - 1;2; - 2;4; - 4;8; - 8} \right\}\)
Câu 4 :
Có bao nhiêu ước của \( - 24.\)
Đáp án : D Phương pháp giải :
Để tìm tất cả các ước của một số nguyên âm ta chỉ cần tìm tất cả các ước của số đối của số nguyên âm đó. Trước tiên ta tìm ước tự nhiên rồi thêm các ước đối của chúng. Lời giải chi tiết :
Có \(8\) ước tự nhiên của \(24\) là: \(1;2;3;4;6;8;12;24\) Có \(8\) ước nguyên âm của \(24\) là: \(-1;-2;-3;-4;-6;-8;-12;-24\) Vậy có \(8.2 = 16\) ước của \( 24\) nên cũng có $16$ ước của $-24.$
Câu 5 :
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
Đáp án : A Phương pháp giải :
+ Bước 1: Tìm ước của \(9\) Lời giải chi tiết :
$a + 4$ là ước của $9$  Vậy giá trị lớn nhất của \(a\) là \(a = 5\)
Câu 6 :
Cho \(x \in \mathbb{Z}\) và \(\left( { - 154 + x} \right) \vdots \, 3\) thì:
Đáp án : A Phương pháp giải :
Sử dụng tính chất chia hết trong tập hợp các số nguyên $a \, \vdots \, m;b \, \vdots \, m \Rightarrow (a + b) \, \vdots \, m$ Lời giải chi tiết :
Ta có: \(\left( { - 154 + x} \right) \, \vdots \, 3\) \(\left( { - 153 - 1 + x} \right) \, \vdots \, 3\) Suy ra \(\left( {x - 1} \right) \, \vdots \, 3\) (do \( - 153 \, \vdots \, 3\)) Do đó \(x - 1 = 3k \Rightarrow x = 3k + 1\) Vậy \(x\) chia cho \(3\) dư \(1.\)
Câu 7 :
Tìm $n \in Z,$ biết: $\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$
Đáp án : B Phương pháp giải :
Bước 1: Phân tích $n + 5$ về dạng $a.\left( {n + 1} \right) + b{\rm{ }}\left( {a,b\; \in \;Z,a \ne 0} \right)$ Lời giải chi tiết :
$\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$$ \Rightarrow \left( {n + 1} \right) + 4 \, \vdots \, \left( {n{\rm{ }} + 1} \right)$ Vì \(n + 1 \, \vdots \, n + 1\) và \(n \in Z\) nên để \(n + 5 \, \vdots \, n + 1\) thì \(4 \, \vdots \, n + 1\) Hay \(n + 1 \in U\left( 4 \right) = \left\{ { \pm 1; \pm 2; \pm 4} \right\}\) Ta có bảng:  Vậy \(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\)
Câu 8 :
Có bao nhiêu số nguyên $a < 5$ biết: $10$ là bội của $\left( {2a + 5} \right)$
Đáp án : A Phương pháp giải :
\(10\) là bội của \(2a + 5\) nghĩa là \(2a + 5\) là ước của \(10\) - Tìm các ước của \(10\) - Lập bảng tìm \(a,\) đối chiếu điều kiện và kết luận. Lời giải chi tiết :
Vì \(10\) là bội của \(2a + 5\) nên \(2a + 5\) là ước của \(10\) \(U\left( {10} \right) = \left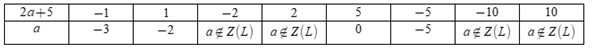\{ { \pm 1; \pm 2; \pm 5; \pm 10} \right\}\) Ta có bảng:  Mà \(a < 5\) nên \(a \in \left\{ { - 3; - 2;0; - 5} \right\}\) Vậy có \(4\) giá trị nguyên của \(a\) thỏa mãn bài toán.
Câu 9 :
Tìm $x,$ biết: $x \, \vdots \, 6$ và $24 \, \vdots \, x$
Đáp án : B Phương pháp giải :
- Tìm tập hợp các bội của \(6\) - Tìm tập hợp các ước của \(24\) - Lấy giao hai tập trên ta được đáp án. Lời giải chi tiết :
Ta có: \(A = B\left( 6 \right) = \left\{ {0; \pm 6; \pm 12; \pm 18; \pm 24;...} \right\}\) \(B = Ư\left( {24} \right) = \left\{ { \pm 1; \pm 2; \pm 3; \pm 4; \pm 6; \pm 8; \pm 12; \pm 24} \right\}\) Vậy \(x \in A \cap B = \left\{ { \pm 6; \pm 12; \pm 24} \right\}\)
Câu 10 :
Cho \(a\) và \(b\) là hai số nguyên khác \(0.\) Biết \(a \, \vdots \, b\) và \(b \, \vdots \, a.\) Khi đó
Đáp án : D Phương pháp giải :
Sử dụng định nghĩa chia hết: \(a \, \vdots \, b\) nếu và chỉ nếu tồn tại số \(q \in Z\) sao cho \(a = b.q\) Lời giải chi tiết :
Ta có: \(\begin{array}{l}a \, \vdots \, b \Rightarrow a = b.{q_1}\left( {{q_1} \in Z} \right)\\b \, \vdots \, a \Rightarrow b = a.{q_2}\left( {{q_2} \in Z} \right)\end{array}\) Suy ra \(a = b.{q_1} = \left( {a.{q_2}} \right).{q_1} = a.\left( {{q_1}{q_2}} \right)\) Vì \(a \ne 0\) nên \(a = a\left( {{q_1}{q_2}} \right) \Rightarrow 1 = {q_1}{q_2}\) Mà \({q_1},{q_2} \in Z\) nên \({q_1} = {q_2} = 1\) hoặc \({q_1} = {q_2} = - 1\) Do đó \(a = b\) hoặc \(a = - b\)
Câu 11 :
Gọi \(A\) là tập hợp các giá trị $n \in Z$ để \(\left( {{n^2} - 7} \right)\) là bội của \(\left( {n + 3} \right)\). Tổng các phần tử của \(A\) bằng:
Đáp án : A Phương pháp giải :
Biến đổi biểu thức \({n^2} - 7\) về dạng \(a.\left( {n + 3} \right) + b\) với \(b \in Z\) rồi suy ra \(n + 3\) là ước của \(b\) Lời giải chi tiết :
Ta có:\({n^2} - 7 = {n^2} + 3n - 3n - 9 + 2\)\( = n\left( {n + 3} \right) - 3\left( {n + 3} \right) + 2\)\( = \left( {n - 3} \right)\left( {n + 3} \right) + 2\) Vì \(n \in Z\) nên để \({n^2} - 7\) là bội của \(n + 3\) thì \(2\) là bội của \(n + 3\) hay \(n + 3\) là ước của \(2\) \(Ư\left( 2 \right) = \left\{ { \pm 1; \pm 2} \right\}\) nên \(n + 3 \in \left\{ { \pm 1; \pm 2} \right\}\) Ta có bảng:  Vậy \(n \in A = \left\{ { - 5; - 4; - 2; - 1} \right\}\) Do đó tổng các phần tử của \(A\) là \(\left( { - 5} \right) + \left( { - 4} \right) + \left( { - 2} \right) + \left( { - 1} \right) = - 12\)
Câu 12 :
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
Đáp án : C Phương pháp giải :
+ Biến đổi để tách \(5x + 46y\) thành tổng của hai số, trong đó một số chia hết cho $16$ và một số chứa nhân tử \(x + 6y\) + Sử dụng tính chất chia hết trên tập hợp các số nguyên để chứng minh. Lời giải chi tiết :
Ta có: \(\begin{array}{l}5x + 46y = 5x + 30y + 16y\\ = \left( {5x + 30y} \right) + 16y\\ = 5\left( {x + 6y} \right) + 16y\end{array}\) Vì \(5x + 46y\) chia hết cho $16$ và $16y$ chia hết cho $16$ nên suy ra \(5\left( {x + 6y} \right)\) chia hết cho $16.$ Mà $5$ không chia hết cho $16$ nên suy ra \(x + 6y\) chia hết cho $16$ Vậy nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) cũng chia hết cho $16.$
Câu 13 :
Có bao nhiêu số nguyên \(n\) thỏa mãn \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(\left( {n - 1} \right)?\)
Đáp án : C Phương pháp giải :
Áp dụng: \(b\) chia hết cho \(a\) và \(a\) chia hết cho \(b\) thì \(a\),\(b\) là hai số đối nhau (đã chứng minh từ bài tập trước), từ đó suy ra \(n\). Lời giải chi tiết :
Vì \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(n - 1\), Nên \(n - 1\) khác \(0\) và \(n + 5\) khác \(0\) Nên \(n + 5,n - 1\) là hai số đối nhau Do đó: \((n + 5) + (n - 1) = 0\) \(2n + 5 - 1 = 0\) \(2n + 4 = 0\) \(2n = -4\) \(n=-2\) Vậy có 1 số nguyên n thỏa mãn bài toán.
Câu 14 :
Trong các phát biểu sau đây, phát biểu nào đúng?
Đáp án : C Phương pháp giải :
Cho \(a,b \in \mathbb{Z}\) và \(b \ne 0\). Nếu có số nguyên \(q\) sao cho \(a = bq\) thì: Ta nói \(a\) chia hết cho \(b\), kí hiệu là \(a \vdots b\). Lời giải chi tiết :
Ta có: \( - 18 = \left( { - 6} \right).3\) nên \( - 18\) chia hết cho \( - 6\) => C đúng
|
