Lý thuyết Định lí Viète và ứng dụng Toán 9 Kết nối tri thức1. Định lí Viète Nếu ({x_1},{x_2}) là hai nghiệm của phương trình (a{x^2} + bx + c = 0left( {a ne 0} right)) thì (left{ begin{array}{l}{x_1} + {x_2} = - frac{b}{a}\{x_1}{x_2} = frac{c}{a}.end{array} right.) Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh 1. Định lí Viète
Ví dụ: Phương trình 2x2+11x+7=0 có: Δ=112−4.2.7=65>0 nên phương trình có hai nghiệm phân biệt x1,x2. Theo định lí Viète, ta có: x1+x2=−112;x1x2=72. 2. Áp dụng định lí Viète để tính nhẩm nghiệm Giải phương trình bậc hai khi biết một nghiệm của nó
Ví dụ: Phương trình x2−6x+5=0 có a+b+c=1+(−6)+5=0 nên phương trình có hai nghiệm: x1=1,x2=5. Phương trình 5x2+14x+9=0 có a−b+c=5−14+9=0 nên phương trình có hai nghiệm: x1=−1,x2=−95. 3. Tìm hai số khi biết tổng và tích của chúng
Ví dụ: Hai số có tổng bằng 9, tích bằng 20 là nghiệm của phương trình x2+9x+20=0. Ta có: Δ=(−9)2−4.1.20=1,√Δ=1. Suy ra phương trình có hai nghiệm x1=9−12=4;x2=9+12=5. Vậy hai số cần tìm là 4 và 5. 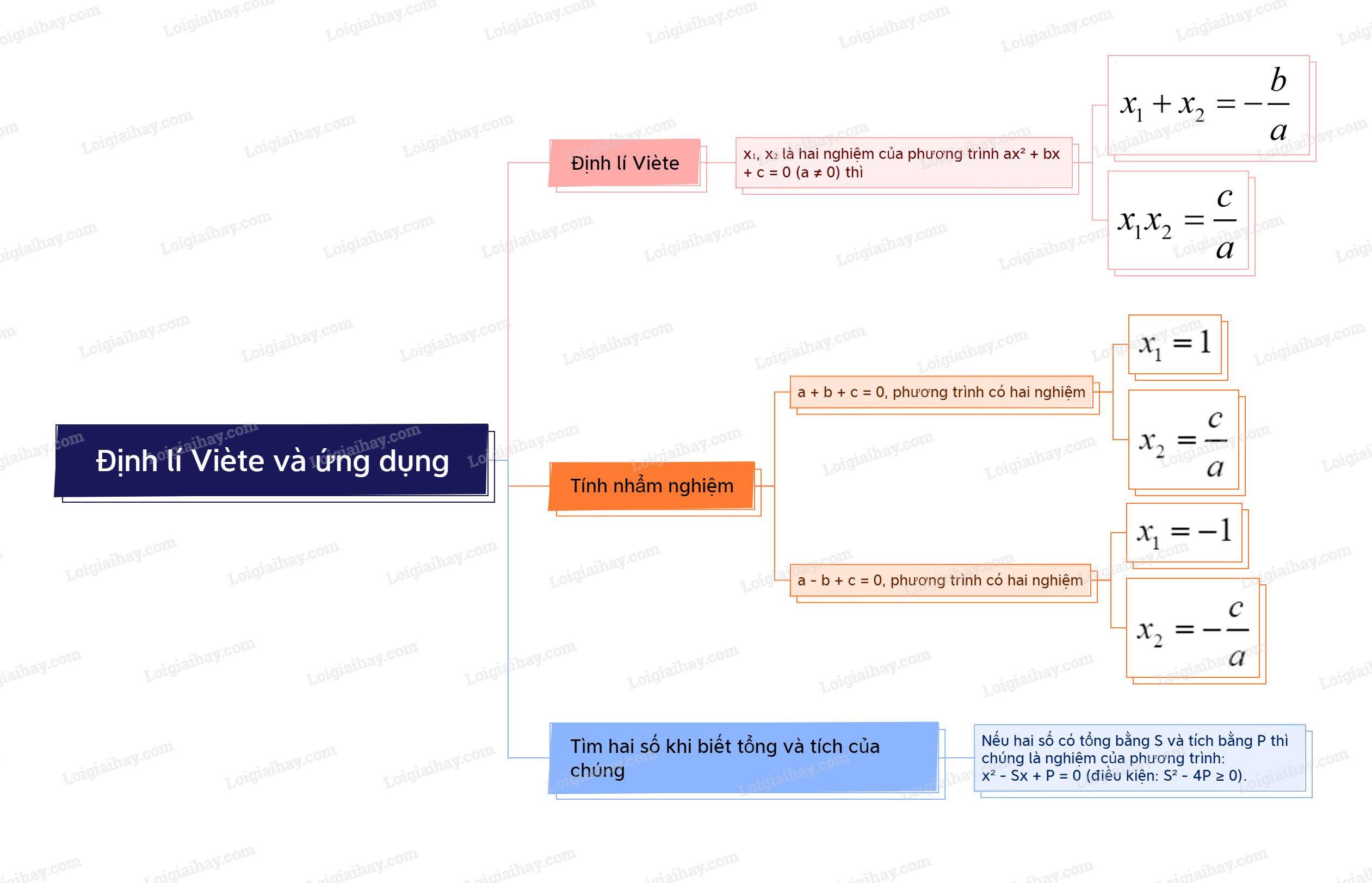
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|





















