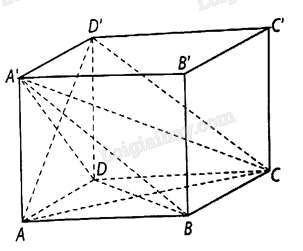
Giải bài 42 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sốngCho hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có \(AB = a,AD = a\sqrt 2 \), góc giữa đường thẳng \(A'C\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({30^ \circ }\). Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Cho hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có \(AB = a,AD = a\sqrt 2 \), góc giữa đường thẳng \(A'C\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({30^ \circ }\). a) Tính theo a thể tích khối hộp chữ nhật. b) Tính theo a khoảng cách giữa hai đường thẳng \(BD\) và \(CD'\). Phương pháp giải - Xem chi tiết
a) Góc giữa đường thẳng \(A'C\) và mặt phẳng \(\left( {ABCD} \right)\) là góc giữa hai đường thẳng \(A'C\) và \(AC\) bằng \(\widehat {A'CA} = {30^ \circ }\)\( \Rightarrow AA'{\rm{\;}}\) Thể tích khối hộp chữ nhật \(ABCD \cdot A'B'C'D'\) bằng \(AB \cdot AD \cdot AA' = \). \({\rm{b)\;V\`i \;}}CD'//\left( {A'BD} \right){\rm{,BD}} \subset {\rm{\;}}\left( {A'BD} \right){\rm{\;}} \Rightarrow d\left( {CD',BD} \right) = d\left( {CD',\left( {A'BD} \right)} \right) = d\left( {D',\left( {A'BD} \right)} \right)\) \(d\left( {D',\left( {A'BD} \right)} \right) = d\left( {{A_,}\left( {A'BD} \right)} \right){\rm{.\;}}\) Đặt \(d\left( {A,\left( {A'BD} \right)} \right) = h\) thì \(\frac{1}{{{h^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} + \frac{1}{{A{A^{{\rm{'}}2}}}} \Rightarrow h\). Kết luận \(d\left( {CD',BD} \right)\). Lời giải chi tiết a) Góc giữa đường thẳng \(A'C\) và mặt phẳng \(\left( {ABCD} \right)\) là góc giữa hai đường thẳng \(A'C\) và \(AC\) bằng \(\widehat {A'CA} = {30^ \circ }\)\( \Rightarrow AA' = AC \cdot {\rm{tan}}{30^ \circ } = a\sqrt 3 \cdot \frac{1}{{\sqrt 3 }} = a{\rm{.\;}}\) Thể tích khối hộp chữ nhật \(ABCD \cdot A'B'C'D'\) bằng \(AB \cdot AD \cdot AA' = {a^3}\sqrt 2 \).
\({\rm{b)\;V\`i \;}}CD'//\left( {A'BD} \right){\rm{,BD}} \subset {\rm{\;}}\left( {A'BD} \right){\rm{\;}} \Rightarrow d\left( {CD',BD} \right) = d\left( {CD',\left( {A'BD} \right)} \right) = d\left( {D',\left( {A'BD} \right)} \right)\) Vì \(D'\) cắt mặt phẳng \(\left( {A'BD} \right)\) tại trung điểm của đoạn \(AD'\) nên \(d\left( {D',\left( {A'BD} \right)} \right) = d\left( {{A_,}\left( {A'BD} \right)} \right){\rm{.\;}}\) Đặt \(d\left( {A,\left( {A'BD} \right)} \right) = h\) thì \(\frac{1}{{{h^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} + \frac{1}{{A{A^{{\rm{'}}2}}}} = \frac{5}{{2{a^2}}} \Rightarrow h = \frac{{a\sqrt {10} }}{5}\). Vậy \(d\left( {CD',BD} \right) = \frac{{a\sqrt {10} }}{5}\).
|