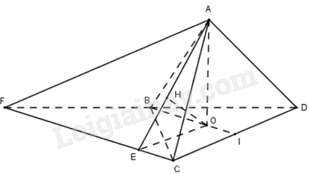
Giải bài 4 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Đề bài

Cho hình tứ diện đều ABCD có cạnh bằng $\sqrt {11}$. Gọi I là trung điểm của cạnh CD. Tính khoảng cách giữa hai đường thẳng AC và BI.

Lời giải chi tiết

Gọi O là tâm của tam giác đều BCD. Khi đó, $AO \bot \left( {BCD} \right)$

Qua C kẻ đường thẳng song song với BI cắt BD tại F. Khi đó, CF//BI nên BI//(ACF)

Suy ra: $d\left( {AC,BI} \right) = d\left( {BI,\left( {ACF} \right)} \right) = d\left( {O,\left( {ACF} \right)} \right)$

Ta có: $BI \bot CD,CF//BI$ $\Rightarrow CF \bot CD$

Qua O kẻ đường thẳng song song với CD cắt CF tại E. Ta có: $OE//CD$ $\Rightarrow OE\; \bot CF$

Vì $OE\; \bot CF,CF \bot AO\left( {do\;AO \bot \left( {BCD} \right)} \right)$ $\Rightarrow CF \bot \left( {AOE} \right)$

Trong (AOE), kẻ $OH \bot AE\left( {H \in AC} \right)$ $\Rightarrow OH \bot \left( {ACF} \right)$ $\Rightarrow d\left( {O,\left( {ACF} \right)} \right) = OH$

Chứng minh được tứ giác OICE là hình chữ nhật. Suy ra $OE = CI = \frac{{CD}}{2} = \frac{{\sqrt {11} }}{2}$

Tam giác BCD đều, BI là đường trung tuyến đồng thời là đường cao của tam giác nên $BI = \frac{{BC\sqrt 3 }}{2} = \frac{{\sqrt {33} }}{2}$ $\Rightarrow BO = \frac{2}{3}BI = \frac{{\sqrt {33} }}{3}$

Vì $AO \bot \left( {BCD} \right)$ $\Rightarrow AO \bot BO,AO \bot OE$.

Áp dụng định lí Pythagore vào tam giác ABO vuông tại O có: $AO = \sqrt {A{B^2} - B{O^2}} = \frac{{\sqrt {66} }}{3}$

Tam giác AOE vuông tại O, đường cao OH có: $\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{E^2}}} = \frac{9}{{66}} + \frac{4}{{11}} = \frac{1}{2}$

Do đó, $OH = \sqrt 2$