Giải bài 7 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Đề bài

Cho hình lăng trụ đều ABC. A’B’C’ có cạnh đáy bằng a. Biết $d\left( {A,\left( {A'BC} \right)} \right) = \frac{{a\sqrt {57} }}{{12}}$. Tính ${V_{ABC.A'B'C'}}$.

Lời giải chi tiết

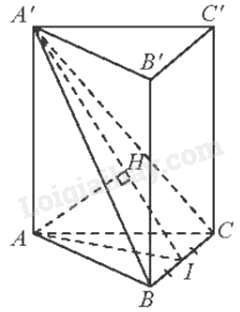
Vì ABC. A’B’C’ là lăng trụ đều $A'A \bot \left( {ABC} \right) \Rightarrow A'A \bot BC$

Gọi I là trung điểm của BC. Tam giác ABC đều nên AI là đường trung tuyến đồng thời là đường cao. Do đó, $AI \bot BC$

Ta có: $A'A \bot BC$, $AI \bot BC$ nên $BC \bot \left( {A'AI} \right)$

Trong mặt phẳng (A’AI), kẻ $AH \bot A'I\left( {H \in A'I} \right) \Rightarrow BC \bot AH$

Vì $BC \bot AH,AH \bot A'I$ nên $AH \bot \left( {A'BC} \right)$. Do đó, $d\left( {A,\left( {A'BC} \right)} \right) = AH = \frac{{a\sqrt {57} }}{{12}}$.

Tam giác ABC đều nên AI là đường trung tuyến đồng thời là đường cao. Do đó, tam giác ABI vuông tại I. Suy ra: $AI = AB.\sin \widehat {ABC} = \frac{{a\sqrt 3 }}{2}$

Vì $A'A \bot \left( {ABC} \right) \Rightarrow A'A \bot AI$

Tam giác A’AI vuông tại A, AH là đường cao có:

$\frac{1}{{A'{A^2}}} = \frac{1}{{A{H^2}}} - \frac{1}{{A{I^2}}} = \frac{{144}}{{57{a^2}}} - \frac{4}{{3{a^2}}} = \frac{{68}}{{57{a^2}}} \\ \Rightarrow A'A = \frac{{a\sqrt {969} }}{{34}}$

Thể tích lăng trụ ABC. A’B’C’ là:  ${V_{ABC.A'B'C'}} = A'A.{S_{ABC}} = A'A.\frac{1}{2}.AI.BC \\ = \frac{1}{2}\frac{{a\sqrt {969} }}{{34}}.\frac{{a\sqrt 3 }}{2}.a = \frac{{3{a^3}\sqrt {323} }}{{136}}$