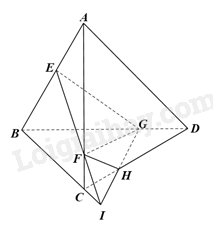
Giải bài 4 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F, G sao cho EB>AE,AF>FC,BG>GD. Tìm giao tuyến của các cặp mặt phẳng (EFG) và (ACD), (EFG) và (BCD), (EFG) và (ABD). Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F, G sao cho EB>AE,AF>FC,BG>GD. Tìm giao tuyến của các cặp mặt phẳng (EFG) và (ACD), (EFG) và (BCD), (EFG) và (ABD). Phương pháp giải - Xem chi tiết Sử dụng kiến thức về giao tuyến giữa hai mặt phẳng để tìm giao tuyến: Đường thẳng d chung giữa hai mặt phẳng (P) và (Q) được gọi là giao tuyến của (P) và (Q), kí hiệu d=(P)∩(Q). Quảng cáo  Lời giải chi tiết
Ta có, EF là giao tuyến của hai mặt phẳng (EFG) và (ABC). Trong mặt phẳng (ABC), gọi I là giao điểm của EF và BC. Trong mặt phẳng (BCD), gọi H là giao điểm của IG và CD. Vì {H∈CD⊂(ACD),H∈IG⊂(EFG)F∈AC⊂(ACD),F∈FE⊂(EFG) nên giao tuyến của hai mặt phẳng (EFG) và (ACD) là FH. Vì {H∈CD⊂(BCD),H∈IG⊂(EFG)G∈BD⊂(BCD),G∈FG⊂(EFG) nên giao tuyến của hai mặt phẳng (EFG) và (BCD) là GH. Vì {E∈AB⊂(ABD),E∈FE⊂(EFG)G∈BD⊂(ABD),G∈FG⊂(EFG) nên giao tuyến của hai mặt phẳng (EFG) và (ABD) là GE.  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
|
