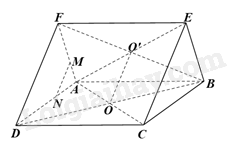
Giải bài 2 trang 121 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Đề bài

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’.

a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE).

b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho $AM = \frac{1}{3}AF,$ $AN = \frac{1}{3}AD$. Chứng minh MN//(DCEF).

Lời giải chi tiết

a) Vì O, O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O là trung điểm của BD, AC và O’ là trung điểm của BF, AE.

Vì O là trung điểm của BD, O’ là trung điểm của BF nên OO’ là đường trung bình của tam giác BDF. Do đó, OO’//DF (1)

Vì O là trung điểm của AC, O’ là trung điểm của AE nên OO’ là đường trung bình của tam giác ACE. Do đó, OO’//CE (2)

Từ (1) và (2) ta có: OO’//DF//CE

Vì OO’//DF, OO’ không nằm trên mặt phẳng (ADF) và $DF \subset \left( {ADF} \right)$ nên OO’//(ADF).

Vì OO’//CE, OO’ không nằm trên mặt phẳng (BCE) và $CE \subset \left( {BCE} \right)$ nên OO’//(BCE).

b) Vì $AM = \frac{1}{3}AF,AN = \frac{1}{3}AD \Rightarrow \frac{{AM}}{{AF}} = \frac{{AN}}{{AD}} = \frac{1}{3}$

Tam giác ADF có: $\frac{{AM}}{{AF}} = \frac{{AN}}{{AD}} = \frac{1}{3}$ nên MN//DF (định lí Thalès đảo)

Vì MN//DF, MN không nằm trên mặt phẳng (DCEF) và $DF \subset \left( {DCEF} \right)$ nên MN//(DCEF).