Đề thi học kì 2 Toán 7 - Đề số 12 - Cánh diềuTổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài
I. Trắc nghiệm
Câu 1 :
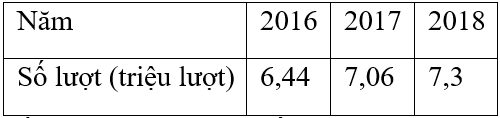
Cho bảng thống kê số lượt khách du lịch (ước đạt) đến Ninh Bình trong các năm 2016, 2017, 2018:
Câu 2 :
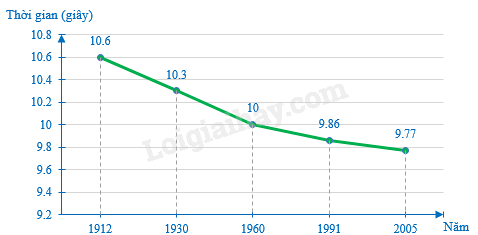
Biểu đồ dưới đây cho biết kỉ lục thế giới về thời gian chạy cự li 100 mét trong các năm từ 1912 đến 2005.
Câu 3 :
Cho hai biểu thức: \(E = 2\left( {a + b} \right) - 4a + 3\) và \(F = 5b - \left( {a - b} \right)\) Khi a = 5 và b = -1. Chọn khẳng định đúng:
Câu 4 :
Biểu thức đại số biểu diễn công thức tính diện tích hình thang có 2 đáy độ dài a, b; chiều cao h ( a, b, h có cùng đơn vị đo độ dài)
Câu 5 :
Hệ số tự do của đa thức \( - {x^7} + 5{x^5} - 12x - 22\) là
Câu 6 :
Giá trị của đa thức \(g\left( x \right) = {x^8}{\rm{ + }}{x^4} + {x^2} + 1\) tại \(x = - 1\) bằng
Câu 7 :
Trong các biến cố sau, biến cố nào là biến cố ngẫu nhiên?
Câu 8 :
Gieo một đồng xu cân đối, đồng chất 1 lần. Xác suất của biến cố “Đồng xu xuất hiện mặt ngửa” là
Câu 9 :
Cho \(\Delta ABC\) vuông tại A có \(\widehat B = {65^0}.\) Chọn khẳng định đúng.
Câu 10 :
Cho tam giác \(ABC\) có AM là đường trung tuyến, trọng tâm \(G\). Khẳng định nào sau đây đúng?
Câu 11 :
Bộ ba số nào là độ dài ba cạnh của một tam giác?
Câu 12 :
Cho \(\Delta ABC\) có \(\widehat A = {35^0};\widehat B = {45^0}\). Số đo góc C là:
II. Tự luận
Câu 1 :
a) Tính giá trị của biểu thức \(A = (2x + y)(2x - y)\) tại \(x = - 2,\;y = \frac{1}{3}.\) b) Tìm tất cả các giá trị của \(x\) thoả mãn \(x(3x - 2) - 3{x^2} = \frac{3}{4}.\)
Câu 2 :
Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2018 – 2022.(Nguồn: Tổng cục thống kê)
a) Tính tổng lượng mưa tại Lai Châu và Cà Mau trong giai đoạn 2018 – 2022. b) Chọn ngẫu nhiên 1 năm trong 5 năm đó, tính xác suất của các biến cố sau: A: “Tại năm được chọn, lượng mưa ở Cà Mau cao hơn ở Lai Châu”. B: “Tại năm được chọn, lượng mưa ở Lai Châu thấp hơn 25m”.
Câu 3 :
Cho hai đa thức \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\) và \(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\) a) Thu gọn hai đa thức \(A\left( x \right)\) và \(B\left( x \right)\) và sắp xếp theo lũy thừa giảm dần của biến. b) Tính \(A\left( x \right) - B\left( x \right)\).
Câu 4 :
Cho tam giác ABC cân tại A. Kẻ \(BH \bot AC;CK \bot AB\) (\(H \in AC;\,\)\(K \in AB\)). a) Chứng minh tam giác AKH là tam giác cân b) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của \(\widehat {BIC}\). c) Chứng minh: \(HK\,{\rm{//}}\,BC\).
Câu 5 :
Tìm tất cả các số nguyên dương \(x,y,z\) thỏa mãn: \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\)và \(200 < {y^2} + {z^2} < 450\). Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Cho bảng thống kê số lượt khách du lịch (ước đạt) đến Ninh Bình trong các năm 2016, 2017, 2018:
Đáp án : C Phương pháp giải :
Tỉnh số lượng khách năm 2018 tăng so với năm 2016. Số lượt khách du lịch đến Ninh Bình trong năm 2018 tăng bao nhiêu phần trăm so với năm 2016 bằng: Số lượt khách tăng : số lượt khách năm 2016 . 100 (%) Lời giải chi tiết :
Số lượt khách du lịch năm 2018 tăng so với năm 2016 là: 7,3 – 6,44 = 0,86 (triệu lượt) Số lượt khách du lịch đến Ninh Bình trong năm 2018 tăng bao nhiêu phần trăm so với năm 2016 là: \(\frac{{0,86}}{{6,44}}.100 = 13,35\left( \% \right)\) Đáp án C.
Câu 2 :
Biểu đồ dưới đây cho biết kỉ lục thế giới về thời gian chạy cự li 100 mét trong các năm từ 1912 đến 2005.
Đáp án : B Phương pháp giải :
Quan sát đồ thị và thực hiện phép tính để xác định. Lời giải chi tiết :
Từ năm 1912 đến năm 2005 kỉ lục thế giới về cự li chạy 100 mét đã giảm là: \(10,6 - 9,77 = 0,83\) (giây) Đáp án B.
Câu 3 :
Cho hai biểu thức: \(E = 2\left( {a + b} \right) - 4a + 3\) và \(F = 5b - \left( {a - b} \right)\) Khi a = 5 và b = -1. Chọn khẳng định đúng:
Đáp án : B Phương pháp giải :
Thay a = 5 và b = -1 vào các biểu thức để tính giá trị và so sánh. Lời giải chi tiết :
Thay a = 5 và b = -1 vào, ta có: \(E = 2.\left( {5 - 1} \right) - 4.5 + 3 = - 9\) \(F = 5.\left( { - 1} \right) - \left( {5 + 1} \right) = - 11\) Vì \( - 9 > - 11\) nên \(E > F\). Đáp án B.
Câu 4 :
Biểu thức đại số biểu diễn công thức tính diện tích hình thang có 2 đáy độ dài a, b; chiều cao h ( a, b, h có cùng đơn vị đo độ dài)
Đáp án : D Phương pháp giải :
Sử dụng công thức tính diện tích hình thang để viết biểu thức. Lời giải chi tiết :
Biểu thức đại số biểu diễn công thức tính diện tích hình thang có 2 đáy độ dài a, b; chiều cao h ( a, b, h có cùng đơn vị đo độ dài) là: \(\frac{{\left( {a + b} \right).h}}{2}\). Đáp án D.
Câu 5 :
Hệ số tự do của đa thức \( - {x^7} + 5{x^5} - 12x - 22\) là
Đáp án : A Phương pháp giải :
Hệ số của hạng tử bậc 0 gọi là hệ số tự do của đa thức đó. Lời giải chi tiết :
Hệ số tự do của đa thức \( - {x^7} + 5{x^5} - 12x - 22\) là – 22. Đáp án A.
Câu 6 :
Giá trị của đa thức \(g\left( x \right) = {x^8}{\rm{ + }}{x^4} + {x^2} + 1\) tại \(x = - 1\) bằng
Đáp án : D Phương pháp giải :
Thay \(x = - 1\) vào đa thức để tính giá trị. Lời giải chi tiết :
Thay \(x = - 1\) vào đa thức g(x) ta được: \(g\left( x \right) = {\left( { - 1} \right)^8}{\rm{ + }}{\left( { - 1} \right)^4} + {\left( { - 1} \right)^2} + 1 = 1 + 1 + 1 + 1 = 4\) Đáp án D.
Câu 7 :
Trong các biến cố sau, biến cố nào là biến cố ngẫu nhiên?
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về các loại biến cố. Lời giải chi tiết :
Biến cố “Gieo hai con xúc xắc 1 lần, tổng số chấm xuất hiện trên hai con xúc xắc là 7” là biến cố ngẫu nhiên. Đáp án D.
Câu 8 :
Gieo một đồng xu cân đối, đồng chất 1 lần. Xác suất của biến cố “Đồng xu xuất hiện mặt ngửa” là
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về xác suất của các biến cố đồng khả năng. Lời giải chi tiết :
Do đồng xu cân đối nên biến cố “Đồng xu xuất hiện mặt ngửa” và “Đồng xu xuất hiện mặt sấp” là đồng khả năng nên xác suất của 2 biến cố này bằng nhau và bằng \(\frac{1}{2}\). Đáp án C.
Câu 9 :
Cho \(\Delta ABC\) vuông tại A có \(\widehat B = {65^0}.\) Chọn khẳng định đúng.
Đáp án : B Phương pháp giải :
Dựa vào mối quan hệ giữa góc và cạnh đối nhau trong một tam giác và định lí tổng ba góc của một tam giác bằng \({180^0}\). Lời giải chi tiết :
Tam giác ABC vuông tại A có \(\widehat B = {65^0}\) nên \(\widehat C = {180^0} - \widehat A - \widehat B = {180^0} - {90^0} - {65^0} = {25^0}\). Vì \(\widehat A > \widehat B > \widehat C\left( {{{90}^0} > {{65}^0} > {{25}^0}} \right)\) nên \(BC > AC > AB\). Đáp án B.
Câu 10 :
Cho tam giác \(ABC\) có AM là đường trung tuyến, trọng tâm \(G\). Khẳng định nào sau đây đúng?
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về trọng tâm của tam giác. Lời giải chi tiết :
Vì G là trọng tâm của tam giác ABC nên \(AG = \frac{2}{3}AM\) suy ra \(GM = AM - AG = AM - \frac{2}{3}AM = \frac{1}{3}AM\). Suy ra \(\frac{{GM}}{{AG}} = \frac{{\frac{1}{3}AM}}{{\frac{2}{3}AM}} = \frac{1}{2}\) hay \(AG = 2GM\). Đáp án B.
Câu 11 :
Bộ ba số nào là độ dài ba cạnh của một tam giác?
Đáp án : C Phương pháp giải :
Dựa vào quan hệ giữa các cạnh của một tam giác. Lời giải chi tiết :
Ta có: 4 + 5 = 9 < 10, ba độ dài \(4cm,\;5cm,\;10cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác. 5 + 5 = 10 < 12, ba độ dài \(5cm,\;5cm,\;12cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác. 11 > 20 – 11 = 9, ba độ dài \(11cm,\;11cm,\;20cm\) thỏa mãn điều kiện của bất đẳng thức tam giác nên đây có thể là độ dài ba cạnh của một tam giác. 11 = 20 – 9, ba độ dài \(9cm,\;20cm,\;11cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác. Đáp án C.
Câu 12 :
Cho \(\Delta ABC\) có \(\widehat A = {35^0};\widehat B = {45^0}\). Số đo góc C là:
Đáp án : D Phương pháp giải :
Dựa vào định lí tổng ba góc của một tam giác bằng \({180^0}\). Lời giải chi tiết :
Số đo góc C là: \(\begin{array}{l}\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {35^0} - {45^0}\\ = {100^0}\end{array}\) Đáp án D.
II. Tự luận
Câu 1 :
a) Tính giá trị của biểu thức \(A = (2x + y)(2x - y)\) tại \(x = - 2,\;y = \frac{1}{3}.\) b) Tìm tất cả các giá trị của \(x\) thoả mãn \(x(3x - 2) - 3{x^2} = \frac{3}{4}.\) Phương pháp giải :
a) Thay \(x = - 2,\;y = \frac{1}{3}\) vào A để tính giá trị biểu thức. b) Sử dụng các phép tính với đa thức một biến để tìm giá trị của x. Lời giải chi tiết :
a) Tại \(x = - 2,\;y = \frac{1}{3}\) ta có \(\begin{array}{l}A = \left[ {2 \cdot ( - 2) + \frac{1}{3}} \right]\left[ {2 \cdot ( - 2) - \frac{1}{3}} \right]\\ = \left( { - 4 + \frac{1}{3}} \right)\left( { - 4 - \frac{1}{3}} \right)\\ = \frac{{ - 11}}{3}.\frac{{ - 13}}{3}\\ = \frac{{143}}{9}.\end{array}\) b) \(x(3x - 2) - 3{x^2} = \frac{3}{4}\) \(\begin{array}{l}3{x^2} - 2x - 3{x^2} = \frac{3}{4}\\ - 2x = \frac{3}{4}\\x = \frac{{ - 3}}{8}.\end{array}\) Vậy \(x = \frac{{ - 3}}{8}\).
Câu 2 :
Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2018 – 2022.(Nguồn: Tổng cục thống kê)
a) Tính tổng lượng mưa tại Lai Châu và Cà Mau trong giai đoạn 2018 – 2022. b) Chọn ngẫu nhiên 1 năm trong 5 năm đó, tính xác suất của các biến cố sau: A: “Tại năm được chọn, lượng mưa ở Cà Mau cao hơn ở Lai Châu”. B: “Tại năm được chọn, lượng mưa ở Lai Châu thấp hơn 25m”. Phương pháp giải :
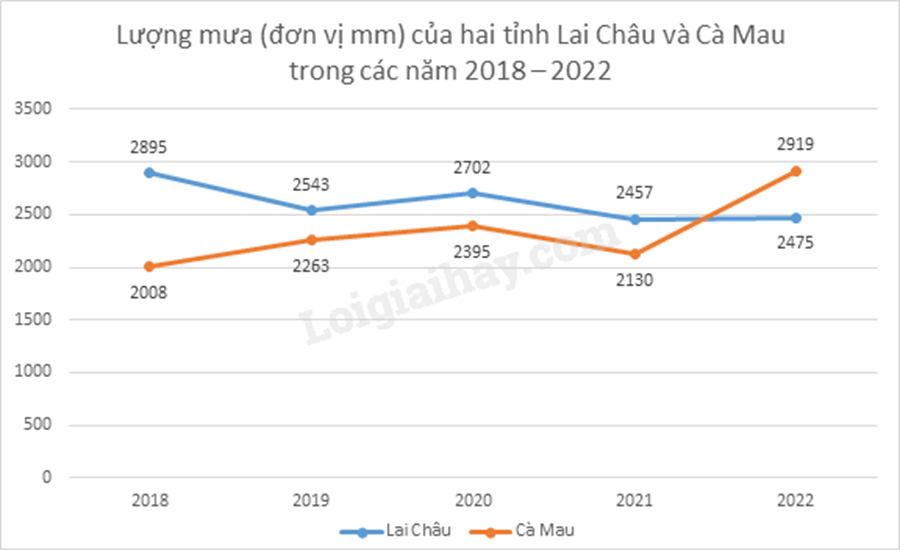
Quan sát đồ thị để trả lời câu hỏi. Lời giải chi tiết :
a) Tổng lượng mưa tại Lai Châu trong giai đoạn 2018 – 2022 là: \(2895 + 2543 + 2702 + 2457 + 2475 = 13072\) (mm) Tổng lượng mưa tại Cà Mau trong giai đoạn 2018 – 2022 là: \(2008 + 2263 + 2395 + 2130 + 2919 = 11715\)(mm) b) Trong 5 năm trên, có 1 năm lượng mưa ở Cà Mau cao hơn ở Lai Châu (năm 2022) nên xác suất của biến cố A là: \(\frac{1}{5}\). Trong 5 năm trên, có 2 năm lượng mưa ở Lai Châu thấp hơn 25m (năm 2021, 2022) nên xác suất của biến cố B là: \(\frac{2}{5}\).
Câu 3 :
Cho hai đa thức \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\) và \(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\) a) Thu gọn hai đa thức \(A\left( x \right)\) và \(B\left( x \right)\) và sắp xếp theo lũy thừa giảm dần của biến. b) Tính \(A\left( x \right) - B\left( x \right)\). Phương pháp giải :
Thực hiện tính toán với đa thức một biến. Lời giải chi tiết :
a) \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\) \(\begin{array}{l} = 5{x^4} + \left( { - 7{x^2} - 6{x^2}} \right) + \left( { - 3x + 11x} \right) - 30\\ = 5{x^4} - 13{x^2} + 8x - 30\end{array}\) \(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\) \(\begin{array}{l} = 13{x^4} + \left( { - 11{x^3} + 20{x^3}} \right) + \left( {5x - 34x} \right) + \left( { - 10 - 2} \right)\\ = 13{x^4} + 9{x^3} - 29x - 12\end{array}\) b) \(A\left( x \right) - B\left( x \right) = \left( {5{x^4} - 13{x^2} + 8x - 30} \right) - \left( {3{x^4} + 9{x^3} - 29x - 12} \right)\) \(\begin{array}{l} = 5{x^4} - 13{x^2} + 8x - 30 - 3{x^4} - 9{x^3} + 29x + 12\\ = \left( {5{x^4} - 3{x^4}} \right) - 9{x^3} - 13{x^2} + \left( {8x + 29x} \right) + \left( { - 30 + 12} \right)\\ = 2{x^4} - 9{x^3} - 13{x^2} + 37x - 18\end{array}\)
Câu 4 :
Cho tam giác ABC cân tại A. Kẻ \(BH \bot AC;CK \bot AB\) (\(H \in AC;\,\)\(K \in AB\)). a) Chứng minh tam giác AKH là tam giác cân b) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của \(\widehat {BIC}\). c) Chứng minh: \(HK\,{\rm{//}}\,BC\). Phương pháp giải :
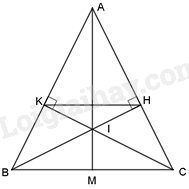
a) Chứng minh \(\Delta ABH = \Delta ACK\) theo trường hợp cạnh huyền – góc nhọn. suy ra AH = AK nên tam giác AKH là tam giác cân. b) Chứng minh \(\widehat {{P_1}} = \widehat {{N_1}}\) nên \(\Delta AKI = \Delta AHI\) theo trường hợp cạnh huyền – cạnh góc vuông suy ra \(\widehat {AIK} = \widehat {AIH}\) Từ đó ta có \(\widehat {CIM} = \widehat {BIM}\) nên IM là phân giác của góc BIC c) Từ tam giác cân ABC và AHK ta có \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\), \(\widehat {AKH} = \frac{{180^\circ - \widehat A}}{2}\) nên \(\widehat {ABC} = \widehat {AKH}\). Mà hai góc này ở vị trí đồng vị nên HK // BC. Lời giải chi tiết :
a) Xét \(\Delta ABH\) và \(\Delta ACK\) có: \(\widehat {AHB} = \widehat {AKC} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\)) AB = AC (\(\Delta ABC\) cân); góc A chung; Do đó: \(\Delta ABH = \Delta ACK\) (cạnh huyền – góc nhọn). \( \Rightarrow AH = AK \Rightarrow \Delta AHK\) cân tại A (đpcm). b) Xét \(\Delta AKI\) và \(\Delta AHI\) có: \(\widehat {AKI} = \widehat {AHI} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\)) AK = AH (\(\Delta AHK\) cân tại A); cạnh AI chung; Do đó: \(\Delta AKI = \Delta AHI\) (cạnh huyền – cạnh góc vuông). \( \Rightarrow \widehat {AIK} = \widehat {AIH}\). Mà: \(\widehat {AIK} = \widehat {CIM};\widehat {AIH} = \widehat {BIM}\) (2 góc đối đỉnh). Do đó: \(\widehat {CIM} = \widehat {BIM}\)\( \Rightarrow IM\)là phân giác của góc BIC (đpcm). c) \(\Delta ABC\) cân tại A nên: \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\) . \(\Delta AHK\) cân tại A nên: \(\widehat {AKH} = \frac{{180^\circ - \widehat A}}{2}\) . Suy ra \(\widehat {ABC} = \widehat {AKH}\). Mà 2 góc này ở vị trí đồng vị. Do đó: KH // BC (đpcm).
Câu 5 :
Tìm tất cả các số nguyên dương \(x,y,z\) thỏa mãn: \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\)và \(200 < {y^2} + {z^2} < 450\). Phương pháp giải :
Biến đổi \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\) thành \(\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4}\). Áp dụng tính chất dãy tỉ số bằng nhau để suy ra \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2} = 0\) Từ đó ta có \(6z = 12x = 8y\). Đặt \(6z = 12x = 8y = 24k\left( {k > 0} \right) \Rightarrow \left( {x;y;z} \right) = \left( {2k;3k;4k} \right)\) Tìm k dựa vào \(200 < {y^2} + {z^2} < 450\) Từ đó tính được x, y, z. Lời giải chi tiết :
Ta có \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\) nên \(\begin{array}{l}\frac{{3\left( {z - 4x} \right)}}{{3.3}} = \frac{{4\left( {3x - 2y} \right)}}{{4.4}} = \frac{{2\left( {4y - 3z} \right)}}{{2.2}}\\\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4}\end{array}\) Áp dụng tính chất dãy tỉ số bằng nhau, ta có: \(\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4} = \frac{{6z - 12x + 12x - 8y + 8y - 6z}}{{9 + 16 + 4}} = \frac{0}{{29}} = 0\) Do đó \(\left\{ \begin{array}{l}6z - 12x = 0\\12x - 8y = 0\\8y - 6z = 0\end{array} \right.\) hay \(6z = 12x = 8y\). Đặt \(6z = 12x = 8y = 24k\left( {k > 0} \right)\) ta được \(\left( {x;y;z} \right) = \left( {2k;3k;4k} \right)\) Theo giả thiết \(200 < {y^2} + {z^2} < 450\) hay \(200 < 9{k^2} + 16{k^2} < 450\) suy ra \(200 < 25{k^2} < 450 \Rightarrow k \in \left\{ {3;4} \right\}\) Từ đó tìm được \(\left( {x;y;z} \right) \in \left\{ {\left( {6;9;12} \right);\left( {8;12;16} \right)} \right\}\)
|
