Đề thi học kì 1 Toán 7 - Đề số 9 - Cánh diềuTải vềPhần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
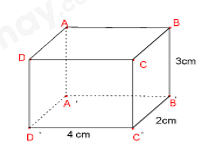
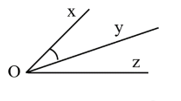
Đề bài Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Trong các câu sau câu nào đúng? A. \(\dfrac{3}{7} \in \mathbb{Q}\) B. \(\dfrac{1}{2} \in \mathbb{Z}\). C. \(\dfrac{{ - 9}}{5} \notin \mathbb{Q}\). D. \( - 6 \in \mathbb{N}\). Câu 2: Tập hợp các số hữu tỉ kí hiệu là: A. N; B. \({N^*}\); C. Q; D. Z. Câu 3: Số đối cùa \(\dfrac{{ - 2}}{3}\) là: A. \(\dfrac{2}{3}\); B. \(\dfrac{3}{2}\); C. \(\dfrac{{ - 3}}{2}\); D. \(\dfrac{2}{{ - 3}}\). Câu 4: Điểm B trên trục số biểu diễn số hữu tỉ nào sau đây? A. \(\dfrac{{ - 2}}{3}\); B. \(\dfrac{{ - 2}}{5}\); C. \( - \dfrac{1}{3}\); D. \(\dfrac{2}{6}\). Câu 5: Phép tính nào sau đây không đúng? A. \({x^{18}}:{x^6} = {x^{12}}\left( {x \ne 0} \right)\) B. \({x^4}.{x^8} = {x^{12}}\) C. \({x^2}.{x^6} = {x^{12}}\) D. \({({x^3})^4} = {x^{12}}\) Câu 6: Cho các số sau \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75;\dfrac{{20}}{{15}} = 1,333....3;\dfrac{5}{4} = 1,25\) số nào viết được dưới dạng số thập phân hữu hạn? A. \(\dfrac{4}{6} = 0,66...6;\dfrac{{20}}{{15}} = 1,333....3\); B. \(\dfrac{3}{4} = 0,75;\dfrac{5}{4} = 1,25\); C. \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75\); D. \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75;\dfrac{{20}}{{15}} = 1,333....3\). Câu 7: Số mặt của hình hộp chữ nhật \(ABCD{A^,}{B^,}{C^,}{D^,}\) là: A. 3; B. 4; C. 6; D. 12. Câu 8: Thể tích của hình hộp chữ nhật bên là: A. 6 cm3; B. 8 cm3; C. 12 cm3; D. 24 cm3. Câu 9: Diện tích xung quanh của hình hộp chữ nhật bên là: A. 12 cm2; B. 24 cm2; C. 36 cm2; D. 42 cm2 Câu 10: Tiên đề Euclid được phát biểu: “Qua một điểm M nằm ngoài đường thẳng a.” A. Có duy nhất một đường thẳng đi qua M và song song với a. B. Có hai đường thẳng song song với a. C. Có ít nhất một đường thẳng song song với a. D. Có vô số đường thẳng song song với a. Câu 11: Hai đại lượng \(x,y\) trong công thức nào tỉ lệ nghịch với nhau: A. \(y = 5 + x\) B. \(x = \dfrac{5}{y}\) C. \(y = 5x\) D. \(x = 5y\) Câu 12: Cho hình vẽ, biết\(\widehat {\;xOy} = {20^0}\), Oy là tia phân giác của góc \(\widehat {xOz}\). Khi đó số đo \(\widehat {yOz\;}\)bằng: A. \({20^0}\) B. \(\;{160^0}\) C. \({80^0}\) D. \(\;{40^0}\).
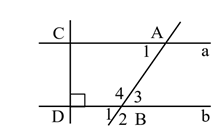
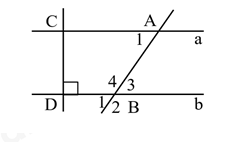
II. TỰ LUẬN (7 điểm) Câu 1: (2 điểm) Tính: a) \(\sqrt 9 - \dfrac{2}{3}\) b) \( - 5 + \sqrt {25} + {2023^0}\) c) \({\left( {\dfrac{1}{4}} \right)^2} \cdot {\left( {\dfrac{1}{2}} \right)^5}:2\) d) \(\left( {2,5 + \dfrac{2}{3}} \right) - 3\dfrac{1}{3}\) Câu 2: (1,5 điểm) Tìm x: a) \(2x - 3,7 = 10\) b) \(\sqrt {49} + 5x - 1 = {\left( { - 2} \right)^3}\) c) \(\dfrac{8}{3}.|2x + 1| = 3\dfrac{1}{3}\) Câu 3: (1,5 điểm) Cửa hàng có 3 tấm vải dài tổng cộng \(126m\). Sau khi bán đi \(\dfrac{1}{2}\) tấm vải thứ nhất, \(\dfrac{2}{3}\) tấm vải thứ hai; \(\dfrac{3}{4}\) tấm vải thứ ba thì số vải còn lại ở cả 3 tấm bằng nhau. Tính chiều dài mỗi tấm vải lúc đầu. Câu 4: (1,5 điểm) Cho hình vẽ sau. Biết a // b. a) Chứng minh CD vuông góc với a. b) Biết số đo góc A1 là 65o. Tính số đo góc B1 ; B2 ; B3 ; B4. Câu 5: (0,5 điểm) Cho các số thực \(a,b,c,d,e\) thỏa mãn: \(\dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{d} = \dfrac{d}{e}\). Chứng minh rằng: \({\left( {\dfrac{{2019b + 2020c - 2021d}}{{2019c + 2020d - 2021e}}} \right)^3} = \dfrac{{{a^2}}}{{bc}}\). Lời giải I. Phần trắc nghiệm (3 điểm)
Câu 1 Phương pháp: Tập hợp các số tự nhiên: N = {0;1;2;3;…} Tập hợp các số nguyên: Z = {-3;-2;-1;0;1;2;3;….} Tập hợp các số hữu tỉ \(Q = \left\{ {\dfrac{a}{b}|a,b \in Z,b \ne 0} \right\}\) Cách giải: \(\dfrac{3}{7} \in \mathbb{Q}\) nên A đúng. \(\dfrac{1}{2} \notin \mathbb{Z}\) nên B sai \(\dfrac{{ - 9}}{5} \in \mathbb{Q}\) nên C sai \( - 6 \notin \mathbb{N}\) nên D sai.
Chọn A. Câu 2 Phương pháp: Tập hợp các số hữu tỉ \(Q = \left\{ {\dfrac{a}{b}|a,b \in Z,b \ne 0} \right\}\) Cách giải: Tập hợp các số hữu tỉ kí hiệu là Q Chọn C. Câu 3 Phương pháp: Hai số đối nhau nếu chúng có tổng là 0. Số đối của số a là số -a. Cách giải: Số đối của \(\dfrac{{ - 2}}{3}\) là \(\dfrac{2}{3}\) Chọn A. Câu 4 Phương pháp: Xác định 1 đơn vị được chia thành bao nhiêu phần. Các số nằm bên trái gốc O là các số âm. Cách giải: Điểm B nằm bên trái gốc O và cách gốc O một khoảng bằng \(\dfrac{1}{3}\) nên điểm B biểu diễn số hữu tỉ \(\dfrac{{ - 1}}{3}\). Chọn C. Câu 5 Phương pháp: Các phép tính với lũy thừa Cách giải: \({x^{18}}:{x^6} = {x^{18 - 6}} = {x^{12}}\left( {x \ne 0} \right)\) nên A đúng \({x^4}.{x^8} = {x^{4 + 8}} = {x^{12}}\) nên B đúng \({x^2}.{x^6} = {x^{2 + 6}} = {x^8}\) nên C sai. \({({x^3})^4} = {x^{3.4}} = {x^{12}}\) nên D đúng. Chọn C. Câu 6 Phương pháp: Nhận biết số thập phân hữu hạn Cách giải: \(\dfrac{4}{6} = 0,66...6\) là số thập phân vô hạn tuần hoàn với chu kì 6. \(\dfrac{3}{4} = 0,75\) là số thập phân hữu hạn. \(\dfrac{{20}}{{15}} = 1,333....3\) là số thập phân vô hạn tuần hoàn với chu kì 3. \(\dfrac{5}{4} = 1,25\) là số thập phân hữu hạn Vậy các số thập phân hữu hạn là \(\dfrac{3}{4} = 0,75\) và \(\dfrac{5}{4} = 1,25\) Chọn B. Câu 7 Phương pháp: Đặc điểm của hình hộp chữ nhật Cách giải: Hình hộp chữ nhật có 6 mặt. Chọn C. Câu 8 Phương pháp: Thể tích hình hộp chữ nhật có kích thước a, b, c là: V = a.b.c Cách giải: Thể tích hình lăng trụ ABCD.A’B’C’D’ là: V = 4.2.3 = 24 (cm3). Chọn D. Câu 9 Phương pháp: Diện tích xung quanh của hình hộp chữ nhật có chiều rộng a, chiều dài b, chiều cao c là: Sxq = 2.(a+b).c Cách giải: Diện tích xung quanh hình hộp chữ nhật là: Sxq = 2.(2+4).3 = 36 (cm2). Chọn C. Câu 10 Phương pháp: Tiên đề Euclid. Cách giải: Qua một điểm M nằm ngoài đường thẳng a, có duy nhất một đường thẳng đi qua M và song song với a. Chọn A. Câu 11 Phương pháp: Vận dụng định nghĩa về đại lượng tỉ lệ nghịch. Cách giải: Ta có: \(x = \dfrac{5}{y}\) là hai đại lượng tỉ lệ nghịch với nhau. Chọn B. Câu 12 Phương pháp: Nếu Om là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOm} = \widehat {yOm} = \dfrac{1}{2}.\widehat {xOy}\) Cách giải: Vì Oy là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {xOy} = \widehat {yOz} = {20^\circ }\) Chọn A.
II. Phần tự luận (7 điểm) Câu 1 Phương pháp: Thực hiện phép tính theo thứ tự thực hiện phép tính. Tính căn bậc hai số học của một số. Cách giải: a) \(\sqrt 9 - \dfrac{2}{3} = 3 - \dfrac{2}{3} = \dfrac{9}{3} - \dfrac{2}{3} = \dfrac{7}{3}\) b) \( - 5 + \sqrt {25} + {2023^0} = - 5 + 5 + 1 = 1\) c) \({\left( {\dfrac{1}{4}} \right)^2} \cdot {\left( {\dfrac{1}{2}} \right)^5}:2 = {\left[ {{{\left( {\dfrac{1}{2}} \right)}^2}} \right]^2}.{\left( {\dfrac{1}{2}} \right)^5}.\dfrac{1}{2} = {\left( {\dfrac{1}{2}} \right)^4}.{\left( {\dfrac{1}{2}} \right)^5}.{\left( {\dfrac{1}{2}} \right)^1} = {\left( {\dfrac{1}{2}} \right)^{4 + 5 + 1}} = {\left( {\dfrac{1}{2}} \right)^{10}}\) d) \(\left( {2,5 + \dfrac{2}{3}} \right) - 3\dfrac{1}{3} = \dfrac{{25}}{{10}} + \dfrac{2}{3} - \dfrac{{10}}{3} = \dfrac{5}{2} - \dfrac{8}{3} = \dfrac{{15}}{6} - \dfrac{{16}}{6} = \dfrac{{ - 1}}{6}\) Câu 2 Phương pháp: \(\left| x \right| = a{\mkern 1mu} \) với \((a > 0)\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = a}\\{x = - a}\end{array}} \right.\) Cách giải: a) \(\begin{array}{*{20}{l}}{2x - 3,7 = 10}\\{2x = 10 + 3,7}\\{2x = 13,7}\\{x = 13,7:2}\\{x = 6,85.}\end{array}\) Vậy x = 6,85. b) \(\begin{array}{*{20}{l}}{\sqrt {49} + 5x - 1 = {{\left( { - 2} \right)}^3}}\\{7 + 5x - 1 = - 8}\\{5x = - 8 - 7 + 1}\\{5x = - 14}\\{x = \dfrac{{ - 14}}{5}}\end{array}\) Vậy \(x = \dfrac{{ - 14}}{5}\) c) \(\begin{array}{*{20}{l}}{\dfrac{8}{3}.|2x + 1| = 3\dfrac{1}{3}}\\{ \Leftrightarrow \dfrac{8}{3}.|2x + 1| = \dfrac{{10}}{3}}\\{ \Leftrightarrow |2x + 1| = \dfrac{{10}}{3}:\dfrac{8}{3}}\\{ \Leftrightarrow |2x + 1| = \dfrac{{10}}{3}.\dfrac{3}{8}}\\{ \Leftrightarrow |2x + 1| = \dfrac{5}{4}}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x + 1 = \dfrac{5}{4}}\\{2x + 1 = \dfrac{{ - 5}}{4}}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = \dfrac{1}{4}}\\{2x = \dfrac{{ - 3}}{2}}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{1}{8}}\\{x = \dfrac{{ - 3}}{4}}\end{array}} \right.}\end{array}\) Vậy \(x \in \left\{ {\dfrac{1}{8};\dfrac{{ - 3}}{4}} \right\}\) Câu 3 Phương pháp: Gọi chiều dài của 3 tấm vải lúc đầu lần lượt là \(a,b,c\,\left( m \right)\) (điều kiện: \(a,b,c > 0\)) Tính chiều dài còn lại của tấm vải thứ nhất, thứ hai và thứ 3 sau khi bán. Lập tỉ lệ thức, áp dụng tính chất của dãy tỉ số bằng nhau, tìm được chiều dài mỗi tâm vải lúc đầu. Cách giải: Gọi chiều dài của 3 tấm vải lúc đầu lần lượt là \(a,b,c\,\left( m \right)\) (điều kiện: \(a,b,c > 0\)) Sau khi bán \(\dfrac{1}{2}\) tấm thì chiều dài tấm vải thứ nhất là: \(\dfrac{a}{2}\,\left( m \right)\) Sau khi bán \(\dfrac{2}{3}\) tấm thì chiều dài tấm vải thứ hai là: \(\dfrac{b}{3}\,\left( m \right)\) Sau khi bán \(\dfrac{3}{4}\) tấm thì chiều dài tấm vải thứ ba là: \(\dfrac{c}{4}\,\left( m \right)\) Theo đề bài ta có: \(\dfrac{a}{2} = \dfrac{b}{3} = \dfrac{c}{4}\) và \(a + b + c = 126\) Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\dfrac{a}{2} = \dfrac{b}{3} = \dfrac{c}{4} = \dfrac{{a + b + c}}{{2 + 3 + 4}} = \dfrac{{126}}{9} = 14\) Từ đó suy ra: \(\dfrac{a}{2} = 14 \Rightarrow a = 14.2 = 28\,\) (thỏa mãn \(a > 0\)) \(\dfrac{b}{3} = 14 \Rightarrow b = 14.3 = 42\) (thỏa mãn \(b > 0\)) \(\dfrac{c}{4} = 14 \Rightarrow c = 14.4 = 56\) (thỏa mãn \(c > 0\)) Vậy chiều dài các tấm vải lần lượt là \(28\,m,\,42m,\,56m\). Câu 4 Phương pháp: Tính chất hai đường thẳng song song: Nếu một đường thẳng cắt đường thẳng song song thì: các góc ở vị trí so le trong bằng nhau, các góc ở vị trí đồng vị bằng nhau, các góc trong cùng phía bù nhau. Tính chất các góc kề bù, các góc đối đỉnh. Cách giải: a) Vì \(a//b,b \bot CD \Rightarrow a \bot CD\) b) Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_3}}\) (2 góc so le trong), mà \(\widehat {{A_1}} = {65^\circ } \Rightarrow \widehat {{B_3}} = {65^\circ }\) Ta có: \(\widehat {{B_3}} = \widehat {{B_1}}\) (2 góc đối đỉnh) nên \(\widehat {{B_1}} = {65^\circ }\). Vì \(\widehat {{B_3}} + \widehat {{B_4}} = {180^\circ }\) (2 góc kề bù) nên \({65^\circ } + \widehat {{B_4}} = {180^\circ } \Leftrightarrow \widehat {{B_4}} = {180^\circ } - {65^\circ } = {115^\circ }\). Mà \(\widehat {{B_2}} = \widehat {{B_4}}\)(2 góc đối đỉnh) nên \(\widehat {{B_2}} = {115^\circ }\). Vậy \(\widehat {{B_1}} = \widehat {{B_3}} = {65^\circ }\); \(\widehat {{B_2}} = \widehat {{B_4}} = {115^\circ }\). Câu 5 Phương pháp: Áp dụng tính chất của dãy tỉ số bằng nhau. Cách giải: Ta có: \(\dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{d} = \dfrac{d}{e}\) nên \(\dfrac{a}{b} = \dfrac{{2019b}}{{2019c}} = \dfrac{{2020c}}{{2020d}} = \dfrac{{2021d}}{{2021e}}\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{{2019b}}{{2019c}} = \dfrac{{2020c}}{{2020d}} = \dfrac{{2021d}}{{2021e}} = \dfrac{{2019b + 2020c - 2021d}}{{2019c + 2020d - 2021e}}\) Mà \(\dfrac{a}{b} = \dfrac{{2019b}}{{2020c}}\) và \(\dfrac{a}{b} = \dfrac{b}{c}\) (gt) nên \({\left( {\dfrac{{2019b + 2020c - 2021d}}{{2019c + 2020d - 2021e}}} \right)^3} = {\left( {\dfrac{a}{b}} \right)^3} = \dfrac{{{a^2}}}{{{b^2}}}.\dfrac{a}{b} = \dfrac{{{a^2}}}{{{b^2}}}.\dfrac{b}{c} = \dfrac{{{a^2}}}{{bc}}\) (đpcm)
|