Đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 10Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài
I. Trắc nghiệm
Câu 1 :
Dựa vào bảng số liệu sau, cho biết tỉ lệ phần trăm học sinh tham gia câu lạc bộ bóng bàn của học sinh khối 7?
Câu 3 :
Một chiếc hộp có chứa 10 chiếc thẻ cùng loại, được đánh số từ 1 đến 10, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp, xét biến cố Y: "Số xuất hiện trên thẻ rút ra là bình phương của một số tự nhiên". Những kết quả thuận lợi cho biến cố Y là:
Câu 4 :
Gieo ngẫu nhiên xúc xắc một lần, xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là bội của \(3\)” là:
Câu 5 :
Tổng số đo các góc của tam giác bằng
Câu 6 :
Cho \(\Delta MNP = \Delta LKQ\), MN = 3cm, MP = 4cm, NP = 5cm, \(\widehat M = {90^0}\). Khi đó:
Câu 7 :
Tam giác ABC có AB = 8cm, BC = 6cm, AC = 4cm. So sánh các góc của tam giác ta có:
Câu 8 :
Bộ ba độ dài nào sau đây là 3 cạnh của một tam giác?
Câu 10 :
Cho tam giác MNK có MN = NK. Khi đó:
Câu 11 :
Cho tam giác ABC cân tại C. Khi đó
Câu 12 :
Đường vuông góc kẻ từ điểm A đến đường thẳng m là
II. Tự luận
Câu 1 :
Lượng điện tiêu thụ mỗi ngày trong 7 ngày đầu tháng \(02/2023\) của một hộ gia đình được cho ở biểu đồ sau:
a) Ngày nào trong tuần đầu tiên của tháng \(02/2023\), hộ gia đình tiêu thụ lượng điện ít nhất? b) Trong tuần đầu tiên của tháng \(02/2023\), hộ gia đình đó tiêu thụ hết bao nhiêu kW.h điện? Trung bình mỗi ngày tiêu thụ bao nhiêu kW.h điện? c) Trong 7 ngày đầu tiên của tháng \(02/2023\), ngày tiêu thụ điện nhiều nhất tăng bao nhiêu % so với ngày tiêu thụ điện ít nhất?
Câu 2 :
Một bình có 5 quả bóng có kích thước và khối lượng giống nhau, trong đó có 1 quả màu xanh, 1 quả màu vàng, 1 quả màu đỏ, và 1 quả màu trắng, 1 quả màu đen. Lấy ra ngẫu nhiên 1 quả bóng từ bình. a) Gọi A là biến cố: “Lấy được quả bóng màu vàng”. Tính xác suất của biến cố A. b) Gọi B là biến cố “ Quả bóng lấy ra không có màu hồng”. Tính xác suất của biến cố B.
Câu 3 :
Ba thành phố ở ba địa điểm A, B, C không thẳng hàng như hình vẽ, biết AC = 30 km, AB = 90 km. Nếu đặt ở địa điểm C máy phát sóng truyền thanh có bán kính hoạt động 60km thì thành phố B có nhận được tín hiệu không? Vì sao?
Câu 4 :
Cho ∆DFE cân tại E. Gọi M là trung điểm của DF.
Câu 5 :
Cho ba số a, b, c khác 0 thỏa mãn: \(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ca}}{{c + a}}\). Tính giá trị của biểu thức \(M = \frac{{2ab + 3bc + ca}}{{2{a^2} + 3{b^2} + {c^2}}}\). Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Dựa vào bảng số liệu sau, cho biết tỉ lệ phần trăm học sinh tham gia câu lạc bộ bóng bàn của học sinh khối 7?
Đáp án : C Phương pháp giải :
Quan sát bảng số liệu để trả lời. Lời giải chi tiết :
Tỉ lệ phần trăm học sinh tham gia câu lạc bộ bóng bàn của học sinh khối 7 là 22%.
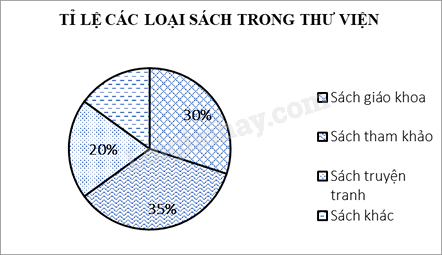
Đáp án : C Phương pháp giải :
Quan sát đồ thị để trả lời. Lời giải chi tiết :
Các loại sách khác chiếm số phần trăm là: 100% - 20% - 35% - 30% = 15%.
Câu 3 :
Một chiếc hộp có chứa 10 chiếc thẻ cùng loại, được đánh số từ 1 đến 10, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp, xét biến cố Y: "Số xuất hiện trên thẻ rút ra là bình phương của một số tự nhiên". Những kết quả thuận lợi cho biến cố Y là:
Đáp án : A Phương pháp giải :
Liệt kê các số là bình phương của một số tự nhiên từ 1 đến 10. Lời giải chi tiết :
Kết quả thuận lợi cho biến cố Y là: 1; 4; 9.
Câu 4 :
Gieo ngẫu nhiên xúc xắc một lần, xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là bội của \(3\)” là:
Đáp án : B Phương pháp giải :
Chỉ ra số kết quả có thể, số kết quả thuận lợi cho biến cố X để tính xác suất. Lời giải chi tiết :
Khi gieo một con xúc xắc cân đối thì 6 mặt có khả năng xuất hiện bằng nhau. Ta nói xác suất xuất hiện mỗi mặt của xúc xắc bằng \(\frac{1}{6}\). Các kết quả có khả năng xảy ra của biến cố: “Số chấm xuất hiện là bội của \(3\)” là \(3;6\). Vậy xác suất của biến cố “Số chấm xuất hiện bằng 6” là \(\frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3}\).
Câu 5 :
Tổng số đo các góc của tam giác bằng
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về tổng ba góc của một tam giác. Lời giải chi tiết :
Tổng số đo các góc của tam giác là \({180^0}\).
Câu 6 :
Cho \(\Delta MNP = \Delta LKQ\), MN = 3cm, MP = 4cm, NP = 5cm, \(\widehat M = {90^0}\). Khi đó:
Đáp án : A Phương pháp giải :
Dựa vào đặc điểm của hai tam giác bằng nhau. Lời giải chi tiết :
Ta có \(\Delta MNP = \Delta LKQ\) suy ra \(MN = KL = 3cm;\widehat M = \widehat L = {90^0}\) suy ra đáp án A đúng.
Câu 7 :
Tam giác ABC có AB = 8cm, BC = 6cm, AC = 4cm. So sánh các góc của tam giác ta có:
Đáp án : C Phương pháp giải :
Dựa vào quan hệ giữa góc và cạnh đối diện trong tam giác để so sánh. Lời giải chi tiết :
Trong tam giác ABC có AC < BC < AB (4cm > 6cm > 8cm) suy ra \(\widehat B < \widehat A < \widehat C\).
Câu 8 :
Bộ ba độ dài nào sau đây là 3 cạnh của một tam giác?
Đáp án : C Phương pháp giải :
Dựa vào quan hệ giữa ba cạnh của một tam giác. Lời giải chi tiết :
Ta có 3 + 4 = 7 < 8 nên 3cm, 4cm, 8cm không thể là ba cạnh của một tam giác. Ta có 3 + 7 = 10 nên 10cm, 7cm, 3cm không thể là ba cạnh của một tam giác. Ta có 4 + 5 = 9 nên 9cm, 5cm, 4cm không thể là ba cạnh của một tam giác. Vậy chỉ có 6cm, 7cm, 10cm là ba cạnh của một tam giác.
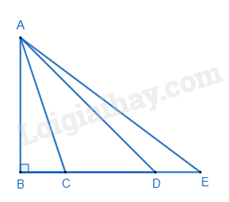
Đáp án : A Phương pháp giải :
Dựa vào mối quan hệ giữa đường vuông góc và đường xiên. Lời giải chi tiết :
Vì AB là đường vuông góc kẻ từ A xuống BE nên AB nhỏ nhất. Quan sát hình vẽ ta thấy C nằm giữa B và D nên BC < BD suy ra AC < AD. Mà D lại nằm giữa B và E nên BD < BE suy ra AD < AE. Suy ra AB < AC < AD < AE.
Câu 10 :
Cho tam giác MNK có MN = NK. Khi đó:
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về tam giác cân. Lời giải chi tiết :
Tam giác MNK có MN = NK là tam giác cân tại N.
Câu 11 :
Cho tam giác ABC cân tại C. Khi đó
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về tam giác cân. Lời giải chi tiết :
Tam giác ABC cân tại C nên \(\widehat A = \widehat B\).
Câu 12 :
Đường vuông góc kẻ từ điểm A đến đường thẳng m là
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về đường vuông góc. Lời giải chi tiết :
Đường vuông góc kẻ từ điểm A đến đường thẳng m là đường thẳng kẻ từ A đến m và vuông góc với m.
II. Tự luận
Câu 1 :
Lượng điện tiêu thụ mỗi ngày trong 7 ngày đầu tháng \(02/2023\) của một hộ gia đình được cho ở biểu đồ sau:
a) Ngày nào trong tuần đầu tiên của tháng \(02/2023\), hộ gia đình tiêu thụ lượng điện ít nhất? b) Trong tuần đầu tiên của tháng \(02/2023\), hộ gia đình đó tiêu thụ hết bao nhiêu kW.h điện? Trung bình mỗi ngày tiêu thụ bao nhiêu kW.h điện? c) Trong 7 ngày đầu tiên của tháng \(02/2023\), ngày tiêu thụ điện nhiều nhất tăng bao nhiêu % so với ngày tiêu thụ điện ít nhất? Phương pháp giải :
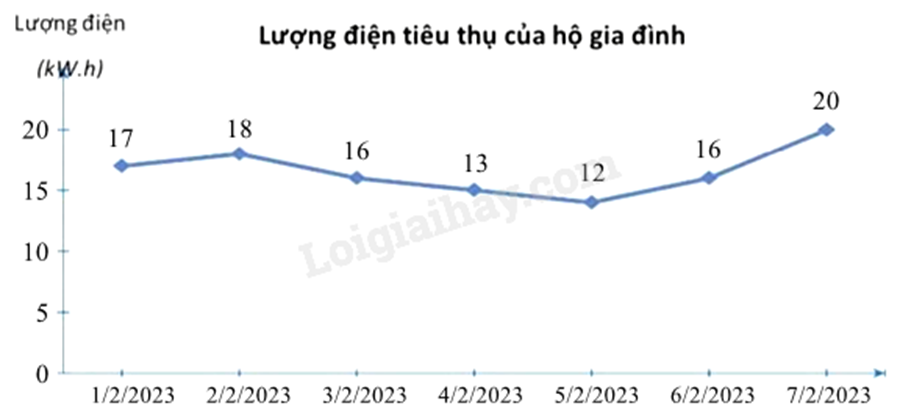
a) Quan sát biểu đồ để trả lời. b) - Tính tổng lượng điện hộ gia đình tiêu thụ cả tuần - Lấy tổng lượng điện chia cho số ngày. c) Tính số phần trăm ngày tiêu thụ nhiều nhất, ít nhất. Lấy số phần trăm ngày tiêu thụ nhiều nhất trừ đi ngày tiêu thụ ít nhất. Lời giải chi tiết :
a) Quan sát biểu đồ ta thấy ngày 5/2/2023 hộ gia đình tiêu thụ lượng điện ít nhất (12kW.h). b) Tổng lượng điện hộ gia đình đó tiêu thụ trong tuần đầu tiên của tháng 02/2023 là: 17 + 18 + 16 + 13 + 12 +16 + 20 = 112 (kW.h) Trung bình mỗi ngày hộ gia đình đó tiêu thụ số lượng điện là: \(\frac{{112}}{7} = 16\) (kW.h) c) Ngày tiêu thụ điện nhiều nhất là 7/2/2023 với 20kW.h. Ngày tiêu thụ điện nhiều nhất chiếm số phần trăm là: \(\frac{{20}}{{112}}.100 \approx 17,86\% \) Ngày tiêu thụ điện ít nhất là 5/2/2023 với 12kW.h. Ngày tiêu thụ điện nhiều nhất chiếm số phần trăm là: \(\frac{{12}}{{112}}.100 \approx 10,71\% \) Ngày tiêu thụ điện nhiều nhất tăng so với ngày tiêu thụ điện ít nhất là: \(17,86\% - 10,71\% = 7,15\% \) Vậy ngày tiêu thụ điện nhiều nhất tăng so với ngày tiêu thụ điện ít nhất khoảng 7,15%.
Câu 2 :
Một bình có 5 quả bóng có kích thước và khối lượng giống nhau, trong đó có 1 quả màu xanh, 1 quả màu vàng, 1 quả màu đỏ, và 1 quả màu trắng, 1 quả màu đen. Lấy ra ngẫu nhiên 1 quả bóng từ bình. a) Gọi A là biến cố: “Lấy được quả bóng màu vàng”. Tính xác suất của biến cố A. b) Gọi B là biến cố “ Quả bóng lấy ra không có màu hồng”. Tính xác suất của biến cố B. Phương pháp giải :
Tìm số kết quả có thể và số kết quả thuận lợi cho biến cố. Lời giải chi tiết :
Có 5 kết quả có thể xảy ra khi lấy ngẫu nhiên 1 quả bóng từ bình là: 1 quả màu xanh, 1 quả màu vàng, 1 quả màu đỏ, và 1 quả màu trắng, 1 quả màu đen. a) Có 1 kết quả thuận lợi cho biến cố A là: 1 quả màu vàng nên xác suất của biến cố A là \(\frac{1}{5}\). b) Tất cả các quả bóng lấy ra đều không có màu hồng nên B là biến cố chắc chắn. Do đó xác suất của biến cố B là \(1\).
Câu 3 :
Ba thành phố ở ba địa điểm A, B, C không thẳng hàng như hình vẽ, biết AC = 30 km, AB = 90 km. Nếu đặt ở địa điểm C máy phát sóng truyền thanh có bán kính hoạt động 60km thì thành phố B có nhận được tín hiệu không? Vì sao?
Phương pháp giải :
Sử dụng hệ quả của bất đẳng thức tam giác. Lời giải chi tiết :
Theo đề bài AC = 30km, AB = 90km suy ra AC < AB. Trong ∆ABC có: CB > AB – AC (hệ quả của bất đẳng thức tam giác) Suy ra CB > 90 – 30 = 60km Vậy nếu đặt tại C máy phát sóng truyền thanh có bán kính hoạt động bằng 60km thì thành phố B không nhận được tín hiệu.
Câu 4 :
Cho ∆DFE cân tại E. Gọi M là trung điểm của DF. Phương pháp giải :
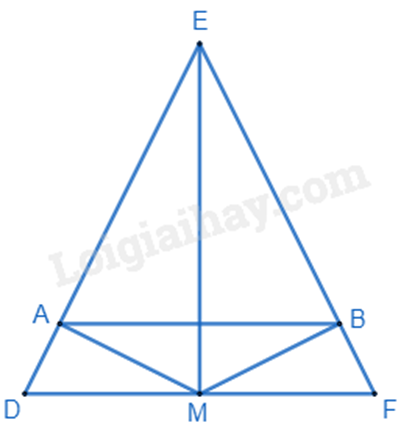
a) Chứng minh \(\Delta EDM{\rm{ }} = {\rm{ }}\Delta EFM\) theo trường hợp cạnh – cạnh – cạnh. b) Chứng minh \(\widehat {EMD} = \widehat {EMF} = {90^0}\) suy ra \(EM \bot DF\). c) Chứng minh \(\Delta EAB\) cân nên \(\widehat {EAB} = \widehat {EDF}\), mà hai góc ở vị trí đồng vị nên AB // DF. Lời giải chi tiết :
a) Xét \(\Delta EDM\) và \(\Delta EFM\) có: DE = EF (tam giác DFE cân tại E) DM = MF (M là trung điểm của DF) ME chung Suy ra \(\Delta EDM = \Delta EFM\) (c.c.c) (đpcm) b) \(\Delta EDM = \Delta EFM\) suy ra \(\widehat {EMD} = \widehat {EMF}\) (hai góc tương ứng) Mà \(\widehat {EMD}\) và \(\widehat {EMF}\) là hai góc kề bù nên \(\widehat {EMD} + \widehat {EMF} = {180^0}\) Suy ra \(\widehat {EMD} = \widehat {EMF} = \frac{{{{180}^0}}}{2} = {90^0}\) hay \(EM \bot DF\) (đpcm) c) \(\Delta EDM = \Delta EFM\) suy ra \(\widehat {DEM} = \widehat {FEM}\) (hai góc tương ứng) Xét \(\Delta AEM\) và \(\Delta BEM\) có: \(\widehat {AEM} = \widehat {BEM}\) (cmt) \(\widehat {EAM} = \widehat {EBM}\left( { = {{90}^0}} \right)\) EM chung Suy ra \(\Delta AEM = \Delta BEM\) (cạnh huyền – góc nhọn) Suy ra AE = EB (hai cạnh tương ứng) suy ra \(\Delta AEB\) là tam giác cân tại E. \(\widehat {EAB} = \widehat {EBA} = \frac{{{{180}^0} - \widehat E}}{2}\) Mà \(\Delta DFE\) cân tại E nên \(\widehat {EDF} = \widehat {EFD} = \frac{{{{180}^0} - \widehat E}}{2}\) Suy ra \(\widehat {EAB} = \widehat {EDF}\). Mà \(\widehat {EAB}\) và \(\widehat {EDF}\) là hai góc đồng vị nên AB // DF (đpcm)
Câu 5 :
Cho ba số a, b, c khác 0 thỏa mãn: \(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ca}}{{c + a}}\). Tính giá trị của biểu thức \(M = \frac{{2ab + 3bc + ca}}{{2{a^2} + 3{b^2} + {c^2}}}\). Phương pháp giải :
Biến đổi \(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ca}}{{c + a}}\) thành \(\frac{{a + b}}{{ab}} = \frac{{b + c}}{{bc}} = \frac{{a + c}}{{ac}}\) và rút gọn để tìm a, b, c. Thay a, b, c vào M để tính giá trị của M. Lời giải chi tiết :
Ta có:\(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ac}}{{a + c}}\) \(\frac{{a + b}}{{ab}} = \frac{{b + c}}{{bc}} = \frac{{a + c}}{{ac}}\) \(\frac{a}{{ab}} + \frac{b}{{ab}} = \frac{b}{{bc}} + \frac{c}{{bc}} = \frac{a}{{ac}} + \frac{c}{{ac}}\) suy ra \(\frac{1}{a} + \frac{1}{b} = \frac{1}{b} + \frac{1}{c} = \frac{1}{a} + \frac{1}{c}\) Ta có \(\frac{1}{a} + \frac{1}{b} = \frac{1}{b} + \frac{1}{c}\) \(\frac{1}{a} = \frac{1}{c}\) suy ra \(a = c\) (1) \(\frac{1}{b} + \frac{1}{c} = \frac{1}{a} + \frac{1}{c}\) \(\frac{1}{a} = \frac{1}{b}\) suy ra \(a = b\) (2) Từ (1) và (2) suy ra a = b = c Thay vào M, ta được: \(\begin{array}{l}M = \frac{{2ab + 3bc + ca}}{{2{a^2} + 3{b^2} + {c^2}}}\\M = \frac{{2.a.a + 3.a.a + a.a}}{{2{a^2} + 3{a^2} + {a^2}}}\\M = \frac{{6{a^2}}}{{6{a^2}}} = 1\end{array}\) Vậy M = 1.
|
