Đề thi học kì 1 Toán 7 - Đề số 5 - Cánh diều

Đề bài

Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1 : Kết quả phép tính \(\dfrac{{ - 5}}{{12}} + \dfrac{{ - 1}}{4}\) bằng

A. \(\dfrac{{ - 1}}{2}\)                                    B. \(\dfrac{{ - 2}}{3}\) 
C. \(\dfrac{1}{2}\)                                          D. \(\dfrac{2}{3}\)

Câu 2 : Giá trị của x thỏa mãn đẳng thức \({x^3} = {\rm{\;}} - 27\) là

A. \(x = 2\)                              B. \(x = {\rm{\;}} - 2\)

C. \(x = 3\)                              D. \(x = {\rm{\;}} - 3\)

Câu 3 : Nếu 15 lít dầu nặng 12kg thì 24kg dầu đó sẽ chứa vừa đầy trong thùng

A. 30 lít                                   B. 27 lít

C. 15 lít                                   D. 13,5 lít

Câu 4 : Cho x và y tỉ lệ thuận với nhau và khi \(x = {\rm{\;}} - 3\)thì \(y = 12\). Hệ số tỉ lệ k của y đối với x là

A. \(k = {\rm{\;}} - 0,25\)                      B. \(k = {\rm{\;}} - 4\)

C. \(k = 0,25\)                         D. \(k = 4\)

Câu 5 : Biết rằng \(\dfrac{{ - 3}}{4} = \dfrac{x}{5}\). Khi đó giá trị của x là

A. \(\dfrac{{ - 15}}{4}\)                                  B. \(\dfrac{{ - 20}}{3}\)

C. \( - 2\)                                      D. \(2\)

Câu 6 : Mặt bên của hình lăng trụ đứng tam giác là hình gì?

A. Tam giác                                        B. Hình vuông

C. Hình chữ nhật                                 D. Hình bình hành

Câu 7 : Cho đường thẳng a cắt hai đường thẳng phân biệt b, c. Số cặp góc đồng vị được tạo ra là

A. 2                             B. 3

C. 4                             D. 6

Câu 8 : Trong các khẳng định sau khẳng định nào sai?

A. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau.

B. Cho a, b, c là 3 đường thẳng phân biệt. Nếu \(a \bot b\) và \(b \bot c\) thì \(a\) // \(c\).

C. Mỗi góc ngoài của một tam giác bằng tổng hai góc trong của tam giác đó.

D. Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.

Câu 9. Thể tích hình hộp chữ nhật có chiều dài 4cm, chiều rộng 3cm, chiều cao 5cm là:

A. 60cm²                     B. 60cm³        C. 35cm²                     D. 35cm³

Câu 10: Số nào là số vô tỉ trong các số sau:

A. \(\dfrac{2}{3}\)                   B. \(\pi \)                    C. \( - \sqrt {16} \)                               D. 0

Câu 11. Cho \(\widehat {xOy}\)  và \(\widehat {yOz}\)  là 2 góc kề bù. Biết \(\widehat {xOy} = {25^0}\) , số đo\(\widehat {yOz}\)   bằng ?

A. 65⁰.             B. 25⁰.                       C. 75⁰                            D. 155⁰.

Câu 12. Cho\(\widehat {xOy} = {70^0}\)  , Ot là tia phân giác của \(\widehat {xOy}\) . Số đo  \(\widehat {xOt}\) bằng ?

A. 35⁰.             B. 30⁰.                       C. 40⁰                            D. 140⁰.

 

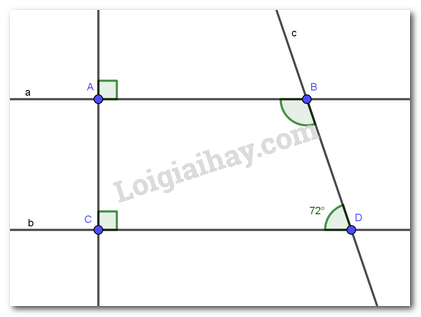
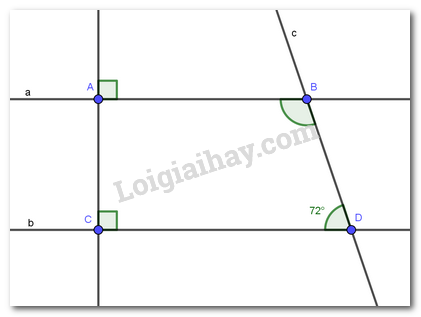
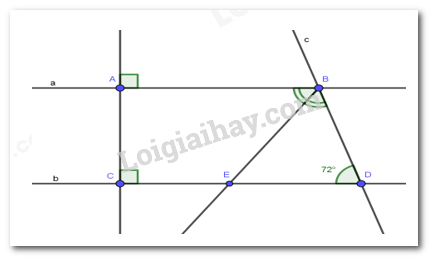
PHẦN II. TỰ LUẬN (7 điểm)

Câu 1 (1,5 điểm): Thực hiện phép tính:         

a) \(\dfrac{7}{6} - \dfrac{1}{6}:\dfrac{2}{3}\)                     

b) \(1\dfrac{3}{4}.\dfrac{2}{7} - 1\dfrac{3}{4}.\dfrac{5}{7}\)

c)\(0,5\sqrt {100} {\rm{\;}} - \dfrac{1}{4}\sqrt {16} {\rm{\;}} + {\left( {\dfrac{{ - 2}}{3}} \right)^2}\)

Câu 2 (1,5 điểm): Tìm x:

a) \(x + \dfrac{2}{5} = \dfrac{3}{{10}}\)

b) \(\dfrac{1}{6}x - 3 = \dfrac{{ - 2}}{3}\)

c) \({\left( {\dfrac{1}{5} - x} \right)^2} = \dfrac{{16}}{9}\)

Câu 3 (1,5 điểm): Ba lớp 7A, 7B, 7C trồng được 180 cây. Tính số cây mỗi lớp trồng được, biết rằng số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5.

Câu 4 (2 điểm)

Cho hình vẽ

 

a)      Chứng minh AB // CD

b)      Tính \(\widehat {ABD}\)

c)      Vẽ tia BE là tia phân giác của \(\widehat {ABD}\) (\(E \in CD\)). Tính \(\widehat {ABE}\)?

Câu 5 (0,5 điểm): Cho ba số a, b, c dương. Chứng tỏ rằng \(M = \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\) không là số nguyên.

Lời giải

I. TRẮC NGHIỆM

1. B	2. D	3. A	4. B	5. A	6. C
7. C	8. C	9. B	10. B	11. D	12. A

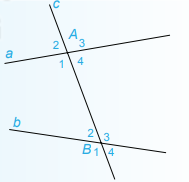
Câu 1:

Phương pháp

Quy đồng phân số rồi tiến hành phép cộng hai phân số cùng mẫu.

Lời giải

\(\dfrac{{ - 5}}{{12}} + \dfrac{{ - 1}}{4} = \dfrac{{ - 5}}{{12}} + \dfrac{{ - 3}}{{12}} = \dfrac{{ - 8}}{{12}} = \dfrac{{ - 2}}{3}\)

Chọn B.

Câu 2:

Phương pháp

Với m là số lẻ, nếu \({a^m} = {b^m} \Rightarrow a = b\)

Lời giải

\({x^3} = {\rm{\;}} - 27 \Leftrightarrow {x^3} = {\rm{\;}}{\left( { - 3} \right)^3} \Leftrightarrow x =  - 3\)

Vậy \(x =  - 3\).

Câu 3:

Phương pháp

Tính chất hai đại lượng tỉ lệ thuận: \(\dfrac{{{x_1}}}{{{y_1}}} = \dfrac{{{x_2}}}{{{y_2}}}\)

Lời giải

Gọi thể tích thùng dầu đựng vừa đủ 24 kg dầu là x (x > 0).

Vì thể tích và khối lượng dầu là hai đại lượng tỉ lệ thuận nên \(\dfrac{{12}}{{15}} = \dfrac{{24}}{x} \Rightarrow 12.x = 15.24 \Rightarrow x = \dfrac{{15.24}}{{12}} = 30\).

Vậy 24 kg dầu đựng vừa đủ trong thùng 30 lít.

Chọn A.

Câu 4:

Phương pháp

Hệ số tỉ lệ của đại lượng y đối với x là: \(k = \dfrac{y}{x}\)

Lời giải

Hệ số tỉ lệ của y đối với x là: \(k = \dfrac{{12}}{{ - 3}} =  - 4\).

Chọn B.

Câu 5:

Phương pháp

Tính chất của tỉ lệ thức: \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow a.d = b.c\)

Lời giải

\(\dfrac{{ - 3}}{4} = \dfrac{x}{5} \Rightarrow ( - 3).5 = 4.x \Rightarrow x = \dfrac{{ - 15}}{4}\)

Chọn A.

Câu 6:

Phương pháp

Tính chất của hình lăng trụ đứng tam giác.

Lời giải

Mặt bên của hình lăng trụ đứng tam giác là hình chữ nhật.

Chọn C.

Câu 7:

Phương pháp

 

+ Các cặp góc A₁ và B₁ ; A₂ và B₂ ; A₃ và B₃ ; A₄ và B₄ được gọi là các cặp góc đồng vị

Lời giải

Đường thẳng a cắt hai đường thẳng phân biệt b, c tạo thành 4 cặp góc đồng vị, 2 cặp góc so le trong.

Chọn C.

Câu 8:

Phương pháp

Tính chất và dấu hiệu nhận biết hai đường thẳng song song.

Tính chất hai góc kề bù và tia phân giác của một góc.

Lời giải

Xét A. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau nên A đúng.

Xét B. Cho a, b, c là 3 đường thẳng phân biệt. Nếu \(a \bot b\) và \(b \bot c\) thì \(a\) // \(c\) nên B đúng.

Xét C. Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó nên C sai.

Xét D. Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông nên D đúng.

Chọn C.

Câu 9:

Phương pháp

Thể tích hình hộp chữ nhật có kích thước a,b,c là: V = a.b.c

Lời giải

Thể tích hình hộp chữ nhật đó là: V = 4.3.5=60 (cm³)

Chọn B.

Câu 10:

Phương pháp

Viết các số dưới dạng số thập phân

Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn

Lời giải

Số \(\pi  = 3,141592654.....\) là số thập phân vô hạn không tuần hoàn nên là số vô tỉ.

Chọn B.

Câu 11:

Phương pháp

Hai góc kề bù có tổng số đo bằng 180 độ.

Lời giải

Ta có: \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) (2 góc kề bù) nên \(25^\circ  + \widehat {yOz} = 180^\circ  \Rightarrow \widehat {yOz} = 180^\circ  - 25^\circ  = 155^\circ \)

Chọn D.

Câu 11:

Phương pháp

Nếu Ot là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {tOy} = \dfrac{1}{2}.\widehat {xOy}\)

Lời giải

Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {tOy} = \dfrac{1}{2}.\widehat {xOy} = \dfrac{1}{2}.70^\circ  = 35^\circ \)

Chọn A.

II. TỰ LUẬN

Câu 1:

Thực hiện phép tính:           

a) \(\dfrac{7}{6} - \dfrac{1}{6}:\dfrac{2}{3} = \dfrac{7}{6} - \dfrac{1}{6}.\dfrac{3}{2} = \dfrac{7}{6} - \dfrac{1}{4} = \dfrac{{7.2 - 1.3}}{{12}} = \dfrac{{11}}{{12}}\)                  

b) \(1\dfrac{3}{4}.\dfrac{2}{7} - 1\dfrac{3}{4}.\dfrac{5}{7} = \dfrac{7}{4}.\dfrac{2}{7} - \dfrac{7}{4}.\dfrac{5}{7} = \dfrac{2}{4} - \dfrac{5}{4} = {\rm{\;}} - \dfrac{3}{4}\)

c) \(0,5\sqrt {100} {\rm{\;}} - \dfrac{1}{4}\sqrt {16} {\rm{\;}} + {\left( {\dfrac{{ - 2}}{3}} \right)^2}\)

\( = 0,5.10 - \dfrac{1}{4}.4 + \dfrac{4}{9} = 5 - 1 + \dfrac{4}{9}\)

\( = 4 + \dfrac{4}{9} = \dfrac{{4.9 + 4}}{9} = \dfrac{{40}}{9}\)

Câu 2:

Tìm x:

a) \(x + \dfrac{2}{5} = \dfrac{3}{{10}}\)

\( \Leftrightarrow x = \dfrac{3}{{10}} - \dfrac{2}{5} = \dfrac{{3 - 2.2}}{{10}} = \dfrac{{ - 1}}{{10}}\)

b) \(\dfrac{1}{6}x - 3 = \dfrac{{ - 2}}{3}\)

\( \Leftrightarrow \dfrac{1}{6}x = \dfrac{{ - 2}}{3} + 3 = \dfrac{7}{3}\)

\( \Leftrightarrow x = \dfrac{7}{3}.6 = 14\)

c) \({\left( {\dfrac{1}{5} - x} \right)^2} = \dfrac{{16}}{9}\)

\( \Leftrightarrow \left| {\dfrac{1}{5} - x} \right| = \dfrac{4}{3}\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\dfrac{1}{5} - x = \dfrac{4}{3}}\\{\dfrac{1}{5} - x = {\rm{\;}} - \dfrac{4}{3}}\end{array}} \right.\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \dfrac{1}{5} - \dfrac{4}{3}}\\{x = \dfrac{1}{5} + \dfrac{4}{3}}\end{array}} \right.\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = {\rm{\;}} - \dfrac{{17}}{{15}}}\\{x = \dfrac{{23}}{{15}}}\end{array}} \right..\)

\(\begin{array}{*{20}{l}}{d)\;\;\dfrac{{x - 1}}{6} = \dfrac{{x + 3}}{5}}\\{ \Leftrightarrow 5.\left( {x - 1} \right) = 6.\left( {x + 3} \right)}\\{ \Leftrightarrow 5x - 5 = 6x + 18}\\{ \Leftrightarrow 6x - 5x = {\rm{\;}} - 5 - 18}\\{ \Leftrightarrow x = {\rm{\;}} - 23}\end{array}\)

Câu 3:

Ba lớp 7A, 7B, 7C trồng được 180 cây. Tính số cây mỗi lớp trông được, biết rằng số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5.

Gọi số cây ba lớp 7A, 7B, 7C trồng được lần lượt là x, y, z(cây) (\(x,y,z \in {N^*}\))

Ba lớp 7A, 7B, 7C trồng được 180 cây nên \(x + y + z = 180\)

Số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5 nên ta có:

\(x:y:z = 3:4:5\)

\( \Leftrightarrow \dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5} = \dfrac{{x + y + z}}{{3 + 4 + 5}} = \dfrac{{180}}{{12}} = 15\) (Áp dụng tính chất dãy tỉ số bằng nhau)

\( \Rightarrow x = 15.3 = 45{\mkern 1mu} {\mkern 1mu} \)(cây) \(;{\mkern 1mu} {\mkern 1mu} y = 15.4 = 60\) (cây) \(;{\mkern 1mu} {\mkern 1mu} z = 15.5 = 75\) (cây)

Vậy lớp 7A trồng 45 cây, lớp 7B trồng được 60 cây, lớp 7C trồng được 75 cây.

Câu 4:

 

a) Ta có AB\( \bot \) AC (gt)

         CD \( \bot \) AC (gt)

     \( \Rightarrow \) AB // CD

b) Ta có \(\widehat {ABD} + \widehat {BDC} = {180^0}\) (vì AB // CD)

     hay\(\widehat {ABD} + {72^0} = {180^0}\)

              \( \Rightarrow \widehat {ABD} = {108^0}\)

c)

  

Vì BE là tia phân giác của \(\widehat {ABD}\)

Nên \(\widehat {ABE} = \dfrac{{\widehat {ABD}}}{2} = \dfrac{{{{108}^0}}}{2} = {54^0}\)

Câu 5:

Ta có:

\(\begin{array}{*{20}{l}}{\dfrac{a}{{a + b}} > \dfrac{a}{{a + b + c}}}\\{\dfrac{b}{{b + c}} > \dfrac{b}{{a + b + c}}}\\{\dfrac{c}{{c + a}} > \dfrac{c}{{a + b + c}}}\end{array}\)

Cộng vế với vế ta được:

\(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} > \dfrac{a}{{a + b + c}} + \dfrac{b}{{a + b + c}} + \dfrac{c}{{a + b + c}}\)\({\mkern 1mu} \left( { = \dfrac{{a + b + c}}{{a + b + c}} = 1} \right)\)         (1)

Lại có:

\(\begin{array}{*{20}{l}}{\dfrac{a}{{a + b}} < \dfrac{{a + c}}{{a + b + c}}}\\{\dfrac{b}{{b + c}} < \dfrac{{b + a}}{{a + b + c}}}\\{\dfrac{c}{{c + a}} < \dfrac{{c + b}}{{a + b + c}}}\end{array}\)

Cộng vế với vế ta được:

\(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} < \dfrac{{a + c}}{{a + b + c}} + \dfrac{{b + a}}{{a + b + c}} + \dfrac{{c + b}}{{a + b + c}}\)\({\mkern 1mu} \left( { = \dfrac{{2(a + b + c)}}{{a + b + c}} = 2} \right)\)                (2)

Từ (1) và (2) ta có: \(1 < \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} < 2\)

\( \Rightarrow \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\) không phải là số nguyên (đpcm).