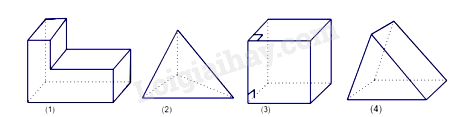
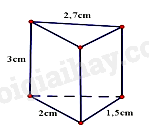
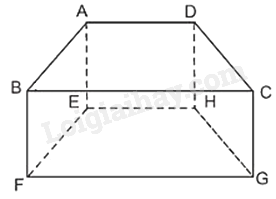
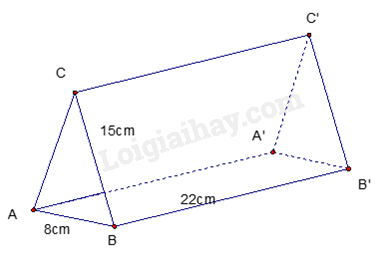
Đề cương ôn tập học kì 1 Toán 7 - Cánh diềuTải vềA. NỘI DUNG ÔN TẬP Đại số Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... A. NỘI DUNG ÔN TẬP Đại số 1. Số hữu tỉ 2. Số thực 3. Tỉ lệ thức Hình học 1. Hình học trực quan 2. Góc và đường thẳng song song B. BÀI TẬP Đề bài I. Phần trắc nghiệm II. Phần tự luận Lời giải chi tiết I. Trắc nghiệm II. Phần tự luận A. NỘI DUNG ÔN TẬPĐại số1. Số hữu tỉ- Cộng, trừ, nhân, chia số hữu tỉ - Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ 2. Số thực- Số vô tỉ - Căn bậc hai số học - Giá trị tuyệt đối của một số thực 3. Tỉ lệ thứcHình học1. Hình học trực quan- Hình hộp chữ nhật – Hình lập phương - Hình lăng trụ đứng tam giác – tứ giác 2. Góc và đường thẳng song song
|
|
Câu 1. A |
Câu 2. A |
Câu 3. C |
Câu 4. C |
Câu 5. D |
|
Câu 6. B |
Câu 7. D |
Câu 8. C |
Câu 9. C |
Câu 10. B |
|
Câu 11. B |
Câu 12. D |
Câu 13. B |
Câu 14. B |
Câu 15. A |
|
Câu 16. D |
Câu 17. D |
Câu 18. A |
Câu 19. C |
Câu 20. C |
|
Câu 21. A |
Câu 22.C |
Câu 23. C |
Câu 24. D |
Câu 25. B |
|
Câu 26. B |
Câu 27. B |
Câu 28. A |
Câu 29. C |
Câu 30. a) C b) C |
|
Câu 31. C |
Câu 32. A |
Câu 33. B |
Câu 34. D |
Câu 35. B |
|
Câu 36. A |
Câu 37. B |
Câu 38. D |
II. Phần tự luận
Bài 1. Tính theo cách hợp lý (nếu có thể):
a) \(\frac{5}{{15}} + \frac{{14}}{{25}} - \frac{4}{3} + \frac{{11}}{{25}}\).
b) \(\frac{5}{{20}} + 1\frac{7}{{11}} - 25\% - \left( {\frac{{18}}{{11}} - \frac{4}{9}} \right)\).
c) \( - \frac{3}{4}.\frac{{12}}{{ - 5}}.\left( { - \frac{{25}}{6}} \right)\).
d) \(2\frac{1}{9}.\frac{2}{3} + 15\frac{8}{9}.\frac{2}{3}\).
e) \(\left( {\frac{{ - 2}}{3} + \frac{3}{{13}}} \right):\frac{7}{8} + \left( {\frac{{ - 1}}{3} + \frac{{10}}{{13}}} \right):\frac{7}{8}\).
f) \(3:{\left( {\frac{{ - 3}}{2}} \right)^2} + \frac{1}{9}.\sqrt {36} + 0,75\).
g) \(\frac{{{{\left( { - 1} \right)}^7}}}{{15}} + {\left( { - \frac{2}{3}} \right)^2}:2\frac{2}{3} - \left| { - \frac{5}{6}} \right|\).
h) \(5:{\left( { - \frac{5}{2}} \right)^2} + \frac{2}{{15}}.\sqrt {\frac{9}{4}} - {\left( { - 2018} \right)^0} + 0,25\).
Phương pháp
- Thực hiện các phép toán với các số hữu tỉ
- Tính lũy thừa của một số hữu tỉ
- Vận dụng kiến thức giá trị tuyệt đối của một số thực:
\(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x > 0\\ - x\,khi\,x < 0\\0\,khi\,x = 0\end{array} \right.\)
- Tính toán căn bậc hai của một số thực
Lời giải
a) \(\frac{5}{{15}} + \frac{{14}}{{25}} - \frac{4}{3} + \frac{{11}}{{25}}\)
\(\begin{array}{l} = \frac{1}{3} + \frac{{14}}{{25}} - \frac{4}{3} + \frac{{11}}{{25}}\\ = \left( {\frac{1}{3} - \frac{4}{3}} \right) + \left( {\frac{{14}}{{25}} + \frac{{11}}{{25}}} \right)\\ = - 1 + 1\\ = 0\end{array}\)
b) \(\frac{5}{{20}} + 1\frac{7}{{11}} - 25\% - \left( {\frac{{18}}{{11}} - \frac{4}{9}} \right)\)
\(\begin{array}{l} = \frac{1}{4} + \frac{{18}}{{11}} - \frac{1}{4} - \frac{{18}}{{11}} + \frac{4}{9}\\ = \left( {\frac{1}{4} - \frac{1}{4}} \right) + \left( {\frac{{18}}{{11}} - \frac{{18}}{{11}}} \right) + \frac{4}{9}\\ = \frac{4}{9}\end{array}\)
c) \( - \frac{3}{4}.\frac{{12}}{{ - 5}}.\left( { - \frac{{25}}{6}} \right)\)
\(\begin{array}{l} = \frac{{ - 3.12.\left( { - 25} \right)}}{{4.\left( { - 5} \right).6}}\\ = \frac{{{{3.3.4.5}^2}}}{{4.\left( { - 5} \right).2.3}}\\ = \frac{{3.5}}{{ - 2}}\\ = \frac{{ - 15}}{2}\end{array}\)
d) \(2\frac{1}{9}.\frac{2}{3} + 15\frac{8}{9}.\frac{2}{3}\)
\(\begin{array}{l} = \left( {2\frac{1}{9} + 15\frac{8}{9}} \right).\frac{2}{3}\\ = \left[ {\left( {2 + 15} \right) + \left( {\frac{1}{9} + \frac{8}{9}} \right)} \right].\frac{2}{3}\\ = \left( {17 + 1} \right).\frac{2}{3}\\ = 18.\frac{2}{3}\\ = 12\end{array}\)
e) \(\left( {\frac{{ - 2}}{3} + \frac{3}{{13}}} \right):\frac{7}{8} + \left( {\frac{{ - 1}}{3} + \frac{{10}}{{13}}} \right):\frac{7}{8}\)
\(\begin{array}{l} = \left( {\frac{{ - 2}}{3} + \frac{3}{{13}} + \frac{{ - 1}}{3} + \frac{{10}}{{13}}} \right):\frac{7}{8}\\ = \left[ {\left( {\frac{{ - 2}}{3} + \frac{{ - 1}}{3}} \right) + \left( {\frac{3}{{13}} + \frac{{10}}{{13}}} \right)} \right]:\frac{7}{8}\\ = \left( { - 1 + 1} \right):\frac{7}{8}\\ = 0:\frac{7}{8}\\ = 0\end{array}\)
f) \(3:{\left( {\frac{{ - 3}}{2}} \right)^2} + \frac{1}{9}.\sqrt {36} + 0,75\)
\(\begin{array}{l} = 3:\frac{9}{4} + \frac{1}{9}.6 + \frac{3}{4}\\ = 3.\frac{4}{9} + \frac{6}{9} + \frac{3}{4}\\ = \frac{4}{3} + \frac{2}{3} + \frac{3}{4}\\ = 2 + \frac{3}{4}\\ = \frac{{11}}{4}\end{array}\)
g) \(\frac{{{{\left( { - 1} \right)}^7}}}{{15}} + {\left( { - \frac{2}{3}} \right)^2}:2\frac{2}{3} - \left| { - \frac{5}{6}} \right|\)
\(\begin{array}{l} = \frac{{ - 1}}{{15}} + \frac{4}{9}:\frac{8}{3} - \frac{5}{6}\\ = \frac{{ - 1}}{{15}} + \frac{4}{9}.\frac{3}{8} - \frac{5}{6}\\ = \frac{{ - 1}}{{15}} + \frac{1}{6} - \frac{5}{6}\\ = \frac{{ - 1}}{{15}} + \left( {\frac{1}{6} - \frac{5}{6}} \right)\\ = \frac{{ - 1}}{{15}} - \frac{2}{3}\\ = \frac{{ - 11}}{{15}}\end{array}\)
h) \(5:{\left( { - \frac{5}{2}} \right)^2} + \frac{2}{{15}}.\sqrt {\frac{9}{4}} - {\left( { - 2018} \right)^0} + 0,25\)
\(\begin{array}{l} = 5:\frac{{25}}{4} + \frac{2}{{15}}.\frac{3}{2} - 1 + \frac{1}{4}\\ = 5.\frac{4}{{25}} + \frac{1}{5} - 1 + \frac{1}{4}\\ = \frac{4}{5} + \frac{1}{5} - 1 + \frac{1}{4}\\ = 1 - 1 + \frac{1}{4}\\ = \frac{1}{4}\end{array}\)
Bài 2. Tìm x, biết:
a) \(\frac{2}{3} + x = - \frac{1}{{12}}\)
b) \(\frac{5}{{11}}x + 4 = 6\frac{1}{{11}}\)
c) \({\left( {2x + 1} \right)^2} = \frac{{36}}{{25}}\)
d) \({\left( {3x - 1} \right)^3} = - \frac{1}{{27}}\)
e) \(\left| {\frac{1}{2}x - \frac{3}{4}} \right| - 2 = - \frac{3}{2}\)
f) \(\left( {\frac{{15}}{4} - 5x} \right)\left( {9{x^2} - 4} \right) = 0\)
g) \(\sqrt {x - 2} + \frac{1}{3} = 1\) với \(x \ge 2\)
h) \({7^{2x}} + {7^{2x + 3}} = 344\)
i) \(\frac{2}{{x + 3}} - \frac{1}{3} = \frac{{ - 5}}{{12}}\) với \(x \ne - 3\)
j) \(\frac{x}{3} = \frac{{12}}{x}\)
Phương pháp
- Sử dụng kiến thức chuyển vế, tính toán với số hữu tỉ
- Vận dụng kiến thức giá trị tuyệt đối của một số thực:
\(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x > 0\\ - x\,khi\,x < 0\\0\,khi\,x = 0\end{array} \right.\)
- Vận dụng kiến thức căn bậc hai của một số thực
Lời giải
a) \(\frac{2}{3} + x = - \frac{1}{{12}}\)
\(\begin{array}{l}x = - \frac{1}{{12}} - \frac{2}{3}\\x = \frac{{ - 3}}{4}\end{array}\)
Vậy nghiệm của phương trình là \(x = \frac{{ - 3}}{4}\).
b) \(\frac{5}{{11}}x + 4 = 6\frac{1}{{11}}\)
\(\begin{array}{l}\frac{5}{{11}}x = 6\frac{1}{{11}} - 4\\\frac{5}{{11}}x = 2\frac{1}{{11}}\\\frac{5}{{11}}x = \frac{{23}}{{11}}\\x = \frac{{23}}{{11}}:\frac{5}{{11}}\\x = \frac{{23}}{5}\end{array}\)
Vậy nghiệm của phương trình là \(x = \frac{{23}}{5}\).
c) \({\left( {2x + 1} \right)^2} = \frac{{36}}{{25}}\)
\({\left( {2x + 1} \right)^2} = {\left( { \pm \frac{6}{5}} \right)^2}\)
\( \Rightarrow 2x + 1 = \frac{6}{5}\) hoặc \(2x + 1 = - \frac{6}{5}\)
TH1: \(2x + 1 = \frac{6}{5}\)
\(\begin{array}{l}2x = \frac{6}{5} - 1\\2x = \frac{1}{5}\\x = \frac{1}{5}:2\\x = \frac{1}{{10}}\end{array}\)
TH2: \(2x + 1 = - \frac{6}{5}\)
\(\begin{array}{l}2x + 1 = - \frac{6}{5}\\2x = - \frac{6}{5} - 1\\2x = - \frac{{11}}{5}\\x = - \frac{{11}}{5}:2\\x = - \frac{{11}}{{10}}\end{array}\)
Vậy nghiệm của phương trình là \(x \in \left\{ {\frac{1}{{10}}; - \frac{{11}}{{10}}} \right\}\).
d) \({\left( {3x - 1} \right)^3} = - \frac{1}{{27}}\)
\(\begin{array}{l}{\left( {3x - 1} \right)^3} = - \frac{1}{{27}}\\{\left( {3x - 1} \right)^3} = {\left( { - \frac{1}{3}} \right)^3}\\3x - 1 = - \frac{1}{3}\\3x = - \frac{1}{3} + 1\\3x = \frac{2}{3}\\x = \frac{2}{9}\end{array}\)
Vậy nghiệm của phương trình là \(x = \frac{2}{9}\).
e) \(\left| {\frac{1}{2}x - \frac{3}{4}} \right| - 2 = - \frac{3}{2}\)
\(\begin{array}{l}\left| {\frac{1}{2}x - \frac{3}{4}} \right| - 2 = - \frac{3}{2}\\\left| {\frac{1}{2}x - \frac{3}{4}} \right| = - \frac{3}{2} + 2\\\left| {\frac{1}{2}x - \frac{3}{4}} \right| = \frac{1}{2}\end{array}\)
\( \Rightarrow \frac{1}{2}x - \frac{3}{4} = \frac{1}{2}\) hoặc \(\frac{1}{2}x - \frac{3}{4} = - \frac{1}{2}\)
TH1: \(\frac{1}{2}x - \frac{3}{4} = \frac{1}{2}\)
\(\begin{array}{l}\frac{1}{2}x = \frac{1}{2} + \frac{3}{4}\\\frac{1}{2}x = \frac{5}{4}\\x = \frac{5}{4}:\frac{1}{2}\\x = \frac{5}{2}\end{array}\)
TH2: \(\frac{1}{2}x - \frac{3}{4} = - \frac{1}{2}\)
\(\begin{array}{l}\frac{1}{2}x = - \frac{1}{2} + \frac{3}{4}\\\frac{1}{2}x = \frac{1}{4}\\x = \frac{1}{4}:\frac{1}{2}\\x = \frac{1}{2}\end{array}\)
Vậy nghiệm của phương trình là \(x \in \left\{ {\frac{5}{2};\frac{1}{2}} \right\}\).
f) \(\left( {\frac{{15}}{4} - 5x} \right)\left( {9{x^2} - 4} \right) = 0\)
\(\frac{{15}}{4} - 5x = 0\) hoặc \(9{x^2} - 4 = 0\)
TH1: \(\frac{{15}}{4} - 5x = 0\)
\(\begin{array}{l}5x = \frac{{15}}{4}\\x = \frac{3}{4}\end{array}\)
TH2: \(9{x^2} - 4 = 0\)
\(\begin{array}{l}9{x^2} = 4\\{x^2} = \frac{4}{9}\\x = \pm \frac{2}{3}\end{array}\)
Vậy nghiệm của phương trình là \(x \in \left\{ { \pm \frac{2}{3};\frac{3}{4}} \right\}\).
g) \(\sqrt {x - 2} + \frac{1}{3} = 1\) với \(x \ge 2\)
\(\begin{array}{l}\sqrt {x - 2} = \frac{2}{3}\\x - 2 = {\left( {\frac{2}{3}} \right)^2}\\x - 2 = \frac{4}{9}\\x = \frac{{22}}{9}\end{array}\)
Vậy nghiệm của phương trình là \(x = \frac{{22}}{9}\).
h) \({7^{2x}} + {7^{2x + 3}} = 344\)
\(\begin{array}{l}{7^{2x}} + {7^{2x}}{.7^3} = 344\\{7^{2x}} + {343.7^{2x}} = 344\\{7^{2x}}\left( {1 + 343} \right) = 344\\{7^{2x}}.344 = 344\\{7^{2x}} = 1\\{7^{2x}} = {7^0}\\2x = 0\\x = 0\end{array}\)
Vậy nghiệm của phương trình là \(x = 0\).
i) \(\frac{2}{{x + 3}} - \frac{1}{3} = \frac{{ - 5}}{{12}}\) với \(x \ne - 3\)
\(\begin{array}{l}\frac{{2.12}}{{\left( {x + 3} \right).12}} - \frac{{4\left( {x + 3} \right)}}{{3.4\left( {x + 3} \right)}} = \frac{{ - 5\left( {x + 3} \right)}}{{12\left( {x + 3} \right)}}\\\frac{{24 - 4\left( {x + 3} \right)}}{{12\left( {x + 3} \right)}} = \frac{{ - 5\left( {x + 3} \right)}}{{12\left( {x + 3} \right)}}\\ \Rightarrow 24 - 4x - 12 = - 5x - 15\\ - 4x + 5x = - 15 + 12 - 24\\x = - 27\end{array}\)
Vậy nghiệm của phương trình là \(x = - 27\).
j) \(\frac{x}{3} = \frac{{12}}{x}\) (điều kiện: \(x \ne 0\))
\(\begin{array}{l}\frac{x}{3} - \frac{{12}}{x} = 0\\\frac{{{x^2} - 12.3}}{{3x}} = 0\\\frac{{{x^2} - 36}}{{3x}} = 0\\ \Rightarrow {x^2} - 36 = 0\\{x^2} = 36\end{array}\)
\(x = 6\) hoặc \(x = - 6\) (thỏa mãn điều kiện)
Vậy nghiệm của phương trình là \(x \in \left\{ { \pm 6} \right\}\).
Bài 3. Tìm x, y, z biết:
a) \(\frac{x}{2} = \frac{y}{5}\) và \(x + y = - 14\)
b) \(7x = 3y\) và \(x - y = 16\)
c) \(\frac{x}{2} = \frac{y}{3} = \frac{z}{4}\) và \(x + 2y - 3z = - 20\)
d) \(\frac{x}{2} = \frac{y}{3}\) và \(xy = 96\)
e) \(\frac{x}{2} = \frac{y}{3};\frac{y}{5} = \frac{z}{4}\) và \(x - y + z = - 49\)
f) \(2x = 3y = 4z\) và \(x + y + z = 26\)
Phương pháp
Sử dụng tính chất dãy tỉ số bằng nhau.
Lời giải
a) \(\frac{x}{2} = \frac{y}{5}\) và \(x + y = - 14\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2} = \frac{y}{5} = \frac{{x + y}}{{2 + 5}} = \frac{{ - 14}}{7} = - 2\)
\(\begin{array}{l} \Rightarrow \frac{x}{2} = - 2 \Rightarrow x = - 2.2 = - 4\\\frac{y}{5} = - 2 \Rightarrow y = - 2.5 = - 10\end{array}\)
Vậy \(x = - 4;y = - 10\).
b) \(7x = 3y\) và \(x - y = 16\)
Áp dụng tính chất tỉ lệ thức, ta có: \(7x = 3y \Rightarrow \frac{x}{3} = \frac{y}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{3} = \frac{y}{7} = \frac{{x - y}}{{3 - 7}} = \frac{{16}}{{ - 4}} = - 4\)
\(\begin{array}{l} \Rightarrow \frac{x}{3} = - 4 \Rightarrow x = - 4.3 = - 12\\\frac{y}{7} = - 4 \Rightarrow y = - 4.7 = - 28\end{array}\)
Vậy \(x = - 12;y = - 28\).
c) \(\frac{x}{2} = \frac{y}{3} = \frac{z}{4}\) và \(x + 2y - 3z = - 20\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2} = \frac{y}{3} = \frac{z}{4} = \frac{{x + 2y - 3z}}{{2 + 2.3 - 3.4}} = \frac{{ - 20}}{{ - 4}} = 5\)
\(\begin{array}{l} \Rightarrow \frac{x}{2} = 5 \Rightarrow x = 5.2 = 10\\\frac{y}{3} = 5 \Rightarrow y = 5.3 = 15\\\frac{z}{4} = 5 \Rightarrow z = 5.4 = 20\end{array}\)
Vậy \(x = 10;y = 15;z = 20\).
d) \(\frac{x}{2} = \frac{y}{3}\) và \(xy = 96\)
Đặt \(\frac{x}{2} = \frac{y}{3} = k\)
\( \Rightarrow \left\{ \begin{array}{l}x = 2k\\y = 3k\end{array} \right.\).
Vì \(xy = 96\) nên ta có: \(2k.3k = 96\)
\(\begin{array}{l} \Rightarrow 6{k^2} = 96\\ \Rightarrow {k^2} = 16\\ \Rightarrow k = \pm 4\end{array}\)
+) Với k = 4, ta có:
\(\left\{ \begin{array}{l}x = 2.4 = 8\\y = 3.4 = 12\end{array} \right.\)
+ Với k = -4, ta có:
\(\left\{ \begin{array}{l}x = 2.\left( { - 4} \right) = - 8\\y = 3.\left( { - 4} \right) = - 12\end{array} \right.\)
Vậy \(\left( {x;y} \right) \in \left\{ {\left( {8;12} \right),\left( { - 8; - 12} \right)} \right\}\).
e) \(\frac{x}{2} = \frac{y}{3};\frac{y}{5} = \frac{z}{4}\) và \(x - y + z = - 49\)
Áp dụng tính chất tỉ lệ thức, ta có:
\(\begin{array}{l}\frac{x}{2} = \frac{y}{3} \Rightarrow 3x = 2y\\\frac{y}{5} = \frac{z}{4} \Rightarrow 4y = 5z\\ \Rightarrow 5z = 4y = 2.2y = 2.3x = 6x\\ \Rightarrow y = \frac{5}{4}z;x = \frac{5}{6}z\end{array}\)
Mà \(x - y + z = - 49\) nên ta có:
\(\begin{array}{l}\frac{5}{6}z - \frac{5}{4}z + z = - 49\\\frac{7}{{12}}z = - 49\\z = - 84\end{array}\)
\(\begin{array}{l} \Rightarrow y = \frac{5}{4}.\left( { - 84} \right) = - 105\\x = \frac{5}{6}.\left( { - 84} \right) = - 70\end{array}\)
Vậy \(x = - 70;y = - 105;z = - 84\).
f) \(2x = 3y = 4z\) và \(x + y + z = 26\)
Ta có:
\(\begin{array}{l}2x = 3y = 4z \Rightarrow \frac{{2x}}{{12}} = \frac{{3y}}{{12}} = \frac{{4z}}{{12}}\\ \Rightarrow \frac{x}{6} = \frac{y}{4} = \frac{z}{3}\end{array}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\begin{array}{l}\frac{x}{6} = \frac{y}{4} = \frac{z}{3} = \frac{{x + y + z}}{{6 + 4 + 3}} = \frac{{26}}{{13}} = 2\\ \Rightarrow \left\{ \begin{array}{l}x = 2.6 = 12\\y = 2.4 = 8\\z = 2.3 = 6\end{array} \right.\end{array}\)
Vậy \(x = 12;y = 8;z = 6\).
Bài 4. Ba nhà sản xuất góp vốn theo tỉ lệ 3; 5; 7. Hỏi mỗi người nhận được bao nhiêu tiền lãi nếu tổng số tiền lãi là 105 triệu đồng và số lãi tỉ lệ thuận với số vốn góp.
Phương pháp
Áp dụng tính chất dãy tỉ số bằng nhau.
Lời giải
Gọi số tiền mà 3 nhà sản xuất nhận được là x, y, z (triệu đồng) \(\left( {0 < x,y,z < 105} \right)\). Khi đó, do tỉ lệ vốn của 3 nhà sản xuất là 3, 5, 7 nên ta có
\(\begin{array}{l}x:y:z = 3:5:7\\ \Leftrightarrow \frac{x}{3} = \frac{y}{5} = \frac{z}{7}\end{array}\)
Lại có 3 nhà sản xuất thu được tổng số tiền lãi là 105 triệu đồng nên ta có
x + y + z = 105
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{x}{3} = \frac{y}{5} = \frac{z}{7} = \frac{{x + y + z}}{{3 + 5 + 7}} = \frac{{105}}{{15}} = 7\)
\( \Rightarrow x = 3.7 = 21,y = 5.7 = 35,z = 7.7 = 49\)
Vậy 3 nhà sản xuất lần lượt nhận đc số tiền là 21 triệu đồng, 35 triệu đồng, và 49 triệu đồng.
Bài 5. Để hưởng ứng phong trào làm xanh môi trường học tập, học sinh lớp 7 cần phải trồng và chăm sóc 40 cây xanh. Lớp 7A có 36 học sinh, lớp 7B có 45 học sinh, lớp 7C có 39 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao nhiêu cây xanh, biết rằng số cây xanh tỉ lệ với số học sinh.
Phương pháp
Sử dụng tính chất của hai đại lượng tỉ lệ thuận.
Áp dụng tính chất dãy tỉ số bằng nhau.
Lời giải
Gọi số cây xanh phải trông và chăm sóc của lớp 7A, 7B, 7C lần lượt là \(x,y,z\left( {x,y,z \in \mathbb{N}*} \right)\) (cây).
Vì số cây xanh tỉ lệ với số học sinh nên ta có:
\(\frac{x}{{36}} = \frac{y}{{45}} = \frac{z}{{39}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\begin{array}{l}\frac{x}{{36}} = \frac{y}{{45}} = \frac{z}{{39}} = \frac{{x + y + z}}{{36 + 45 + 39}} = \frac{{40}}{{120}} = \frac{1}{3}\\ \Rightarrow x = \frac{1}{3}.36 = 12,y = \frac{1}{3}.45 = 15,z = \frac{1}{3}.39 = 13\end{array}\)
Vậy số cây phải trồng và chăm sóc của lớp 7A, 7B, 7C lần lượt là 12 cây, 15 cây và 14 cây.
Bài 6. Ba tổ sản xuất đều được giao công việc như nhau. Tổ 1 hoàn thành công việc trong 5 giờ, tổ 2 hoàn thành công việc trong 6 giờ và tổ 3 hoàn thành công việc trong 8 giờ. Tính số người mỗi tổ, biết năng suất làm việc của mọi người như nhau và cả 3 tổ có 59 người.
Phương pháp
Sử dụng tính chất của các đại lượng tỉ lệ nghịch.
Áp dụng tính chất dãy tỉ số bằng nhau.
Lời giải
Gọi số người mỗi tổ lần lượt là x, y, z (người) \(\left( {x,y,z \in N*} \right)\).
Vì lượng công việc là như nhau nên số người và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch, nên ta có: \(5x = 6y = 8z \Leftrightarrow \frac{x}{{24}} = \frac{y}{{20}} = \frac{z}{{15}}\).
Theo đề bài, ta có: \(x + y + z = 59\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\begin{array}{l}\frac{x}{{24}} = \frac{y}{{20}} = \frac{z}{{15}} = \frac{{x + y + z}}{{24 + 20 + 15}} = \frac{{59}}{{59}} = 1\\ \Rightarrow x = 1.24 = 24,y = 1.20 = 20,z = 1.15 = 15\end{array}\)
Vậy số người của tổ 1, 2, 3 lần lượt là 24 người, 20 người và 15 người.
Bài 7. Nhân dịp Tết Trung Thu, bác Lan đã chuẩn bị đúng số tiền để mua 45 hộc bánh trung thu cùng loại. Nhưng hôm đó cửa hàng đã giảm giá 10% mỗi hộp, hỏi với số tiền đã chuẩn bị thì bác Lan mua được nhiều nhất bao nhiêu hộp bánh trung thu.
Phương pháp
Áp dụng tính chất hai đại lượng tỉ lệ nghịch (số tiền mua mỗi hộp bánh và số bánh mua được) để tính được số bánh mà bác Minh có thể mua được nhiều nhất.
\(\frac{{{x_1}}}{{{x_2}}} = \frac{{{y_2}}}{{{y_1}}}\).
Lời giải
Gọi số hộp bánh trung thu bác Minh dự định mua và mua được nhiều nhất lần lượt là \({x_1},{x_2}\) (hộp) và giá của mỗi hộp bánh trung thu lúc đầu và sau khi giảm giá lần lượt là \({y_1},{y_2}\) (đồng).
Giá của mỗi hộp bánh trung thu sau khi giảm 10% mỗi hộp là:
\({y_2} = {y_1} - {y_1}.10\% = {y_1} - 0,1{y_1} = 0,9{y_1}\)
Do cùng một số tiền nên số hộp bánh mua được và giá của mỗi hộp bánh là hai đại lượng tỉ lệ nghịch nên ta có:
\(\begin{array}{l}\frac{{{x_1}}}{{{x_2}}} = \frac{{{y_2}}}{{{y_1}}} \Rightarrow \frac{{45}}{{{x_2}}} = \frac{{0,9{y_1}}}{{{y_1}}} = 0,9\\ \Rightarrow {x_2} = \frac{{45}}{{0,9}} = 50\end{array}\)
Vậy số hộp bánh mà bác Minh có thể mua được nhiều nhất sau khi giảm giá là 50 hộp bánh.
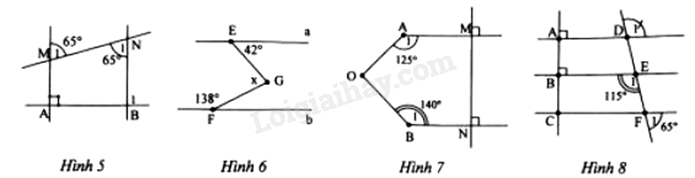
Bài 8. Cho hình vẽ 5, \(\widehat {{M_1}} = \widehat {{N_1}} = {65^0}\). Tính \(\widehat {{B_1}}\).
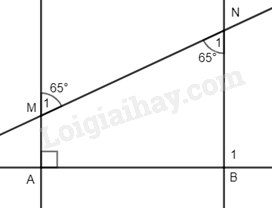
Phương pháp
Sử dụng dấu hiệu nhận biết hai đường thẳng song song.
Tính chất của hai đường thẳng song song.
Lời giải
Ta có: \(\widehat {{M_1}} = \widehat {{N_1}} = {65^0}\).
Mà hai góc này ở vị trí so le trong nên AM // BN.
\( \Rightarrow \widehat {MAB} = \widehat {{B_1}}\) (hai góc đồng vị)
\(\widehat {MAB} = {90^0} \Rightarrow \widehat {{B_1}} = {90^0}\).
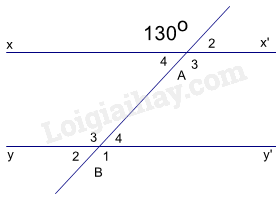
Bài 9. Cho hình vẽ 6, biết a // b. Tính số đo x.
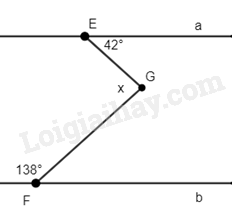
Phương pháp
Kẻ đường thẳng đi qua G song song với a và b.
Sử dụng tính chất của hai đường thẳng song song, hai góc kề bù.
Lời giải
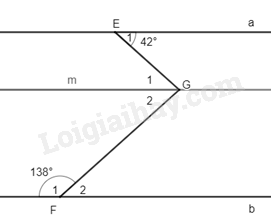
Kẻ đường thẳng m đi qua G và song song với a và b.
Khi đó \(\widehat {{E_1}} = \widehat {{G_1}} = {42^0}\) (hai góc so le trong)
Ta có \(\widehat {{F_1}}\) và \(\widehat {{F_2}}\) là hai góc kề bù \( \Rightarrow \widehat {{F_1}} + \widehat {{F_2}} = {180^0}\)
\( \Rightarrow \widehat {{F_2}} = {180^0} - \widehat {{F_1}} = {180^0} - {138^0} = {42^0}\)
Vì m // b nên \(\widehat {{G_2}} = \widehat {{F_2}} = {42^0}\) (hai góc so le trong)
Mà x = \(\widehat {{G_1}} + \widehat {{G_2}}\)
\( \Rightarrow \widehat {{G_1}} + \widehat {{G_2}} = {42^0} + {42^0} = {84^0}\)
Vậy \(x = {84^0}\).
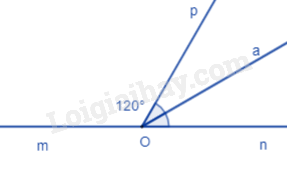
Bài 10. Cho hình vẽ 7. Tính \(\widehat {AOB}\).
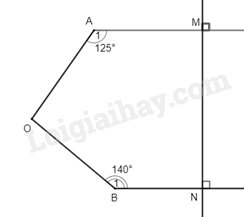
Phương pháp
- Sử dụng dấu hiệu nhận biết hai đường thẳng song song.
- Kẻ đường thẳng đi qua O song song với AM.
- Sử dụng tính chất của hai đường thẳng song song, hai góc kề bù.
Lời giải
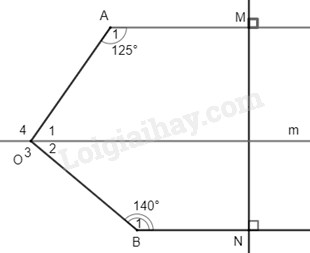
Ta có: \(\widehat M = \widehat N = {90^0}\) (hai góc đồng vị) nên AM // BN.
Qua O kẻ đường thẳng m song song với AM và BN, khi đó:
\(\widehat {{A_1}} = \widehat {{O_4}} = {125^0};\widehat {{B_1}} = \widehat {{O_2}}\) (các cặp góc so le trong)
Mà \(\widehat {{O_1}}\) và \(\widehat {{O_4}}\) là hai góc kề bù nên \(\widehat {{O_1}} + \widehat {{O_4}} = {180^0} \Rightarrow \widehat {{O_1}} = {55^0}\);
\(\widehat {{O_2}}\) và \(\widehat {{O_3}}\) là hai góc kề bù nên \(\widehat {{O_2}} + \widehat {{O_3}} = {180^0} \Rightarrow \widehat {{O_2}} = {40^0}\).
Ta có: \(\widehat {AOB} = \widehat {{O_1}} + \widehat {{O_2}} = {55^0} + {40^0} = {95^0}\).
Vậy \(\widehat {AOB} = {95^0}\).
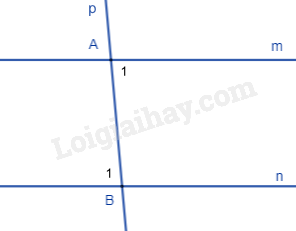
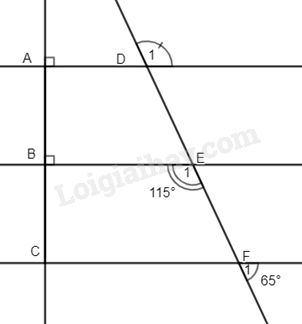
Bài 11. Cho hình vẽ 8.
a) Chứng minh BE // CF.
b) Tính \(\widehat {{D_1}}\).
Phương pháp
a) Sử dụng dấu hiệu nhận biết hai đường thẳng song song, hai góc kề bù.
b) Sử dụng tính chất của hai đường thẳng song song, hai góc đối đỉnh.
Lời giải
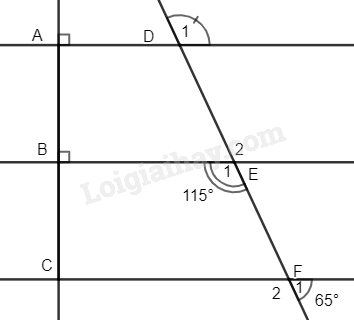
a) Ta có \(\widehat {{F_1}} + \widehat {{F_2}} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {{F_2}} = {180^0} - {65^0} = {115^0}\).
Ta thấy: \(\widehat {{E_1}} = \widehat {{F_2}} = {115^0}\)
Mà \(\widehat {{E_1}}\) và \(\widehat {{F_2}}\) là hai góc ở vị trí đồng vị nên BE // CF (đpcm)
b) Ta có: \(\widehat A = \widehat B = {90^0}\). Mà \(\widehat A\) và \(\widehat B\) ở vị trí đồng vị nên AD // BE.
\( \Rightarrow \widehat {{D_1}} = \widehat {{E_2}}\) (hai góc đồng vị).
Mà \(\widehat {{E_2}} = \widehat {{E_1}} = {115^0}\) (hai góc đối đỉnh)
\( \Rightarrow \widehat {{D_1}} = {115^0}\).
Vậy \(\widehat {{D_1}} = {115^0}\).
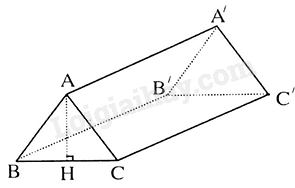
Bài 12. Nhà bạn An có một bể cá hình hộp chữ nhật với kích thước như sau: chiều dài 1,5m; chiều rộng 1,2m; chiều cao 0,9m.
a) Tính thể tích bể cá nhà An.
b) An đổ nước vào bể sao cho khoảng cách từ mặt nước đến miệng bể là 20cm, hỏi An đã đổ bao nhiêu lít nước vào bể cá.
Phương pháp
a) Sử dụng công thức tính thể tích hình hộp chữ nhật.
b) Tính chiều cao nước mà bạn An đổ vào, sử dụng công thức tính thể tích hình hộp chữ nhật để tính số lít nước đổ vào bể cá.
Lời giải
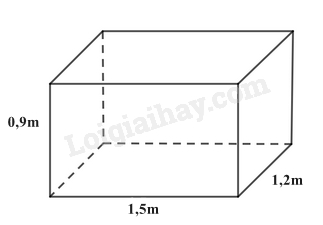
a) Thể tích bể cá nhà An là:
\(V = 1,5.1,2.0,9 = 1,62 \left( {{m^3}} \right)\)
b) Ta có: 20cm = 0,2m nên chiều cao nước mà bạn An đổ vào bể cá là: 0,9 – 0,2 = 0,7 (m)
Thể tích nước mà bạn An đổ vào bể cá là:
\({V_n} = 1,5.1,2.0,7 = 1,26\left( {{m^3}} \right) = 1260(l)\)
Vậy An đã đổ vào bể 1260 lít nước.
Bài 13. Chứng minh rằng: Nếu \(\frac{a}{b} = \frac{c}{d}\) thì:
a) \(\frac{{a + b}}{b} = \frac{{c + d}}{d}\)
b) \(\frac{{a - b}}{a} = \frac{{c - d}}{c}\)
c) \(\frac{{a + b}}{{a - b}} = \frac{{c + d}}{{c - d}}\)
d) \(\frac{{5a + 2b}}{{5a - 2b}} = \frac{{5c + 2d}}{{5c - 2d}}\)
Phương pháp
Sử dụng dấu hiệu nhận biết hai đường thẳng song song.
Tính chất của hai đường thẳng song song.
Lời giải
Ta có: \(\widehat {{M_1}} = \widehat {{N_1}} = {65^0}\).
Bài 14*.
a) Tính GTNN của biểu thức
\(A = 2 + 3\sqrt {{x^2} + 1} \);
\(B = \left| {x - 1} \right| + \left| {x - 3} \right|\)
b) Tính GTLN của biểu thức
\(C = \frac{{5{x^2} + 12}}{{{x^2} + 2}}\);
\(D = 4 - \left| {5x - 2} \right| - \left| {3y + 12} \right|\)
Phương pháp
a) * \(A = 2 + 3\sqrt {{x^2} + 1} \)
Xét giá trị của \({x^2} + 1\) để tính giá trị của \(A = 2 + 3\sqrt {{x^2} + 1} \).
* \(B = \left| {x - 1} \right| + \left| {x - 3} \right|\)
Xét các điểm biểu diễn số thực x trên trục số.
- Khi x nằm ngoài đoạn 1 và 3
- Khi x nằm trong đoạn 1 và 3
b) Biến đổi C, xuất phát từ \({x^2} \ge 0\,\forall x \in \mathbb{R}\) để tính giá trị lớn nhất của C.
Biến đổi D thành \(D = 4 - \left( {\left| {5x - 2} \right| + \left| {3y + 12} \right|} \right)\), tính GTNN của \(\left| {5x - 2} \right| + \left| {3y + 12} \right|\).
Lời giải
* \(A = 2 + 3\sqrt {{x^2} + 1} \)
Ta có:
\(\begin{array}{l}{x^2} \ge 0\,\forall x \in \mathbb{R}\\{x^2} + 1 \ge 1\,\forall x \in \mathbb{R}\\\sqrt {{x^2} + 1} \ge 1\,\forall x \in \mathbb{R}\\2 + 3\sqrt {{x^2} + 1} \ge 2 + 3.1 = 5\,\forall x \in \mathbb{R}\end{array}\)
Dấu “=” xảy ra khi và chỉ khi \({x^2} = 0\) hay \(x = 0\).
Vậy giá trị nhỏ nhất của A là 5 khi x = 0.
* \(B = \left| {x - 1} \right| + \left| {x - 3} \right|\)
Xét các điểm biểu diễn số thực x trên trục số.
Biểu thức đã cho đúng bằng tổng các khoảng cách từ x tới hai điểm 1 và 3
- Nếu x nằm ngoài đoạn giữa 1 và 3 thì tổng khoảng cách trên lớn hơn khoảng cách giữa 1 và 3
- Nếu x nằm trong đoạn giữa 1 và 3 thì tổng khoảng cách nói trên đúng bằng khoảng cách giữa 1 và 3
Vì vậy biểu thức B có giá trị nhỏ nhất là 2, đạt được khi \(1 \le x \le 3\)
b) * \(C = \frac{{5{x^2} + 12}}{{{x^2} + 2}}\)
Ta có: \(C = \frac{{5{x^2} + 12}}{{{x^2} + 2}} = \frac{{5\left( {{x^2} + 1} \right) + 7}}{{{x^2} + 2}} = 5 + \frac{7}{{{x^2} + 2}}\)
Ta có:
\(\begin{array}{l}{x^2} \ge 0\,\forall x \in \mathbb{R}\\{x^2} + 2 \ge 2\,\forall x \in \mathbb{R}\\\frac{1}{{{x^2} + 2}} \le \frac{1}{2}\forall x \in \mathbb{R}\\\frac{7}{{{x^2} + 2}} \le \frac{7}{2}\forall x \in \mathbb{R}\\5 + \frac{7}{{{x^2} + 2}} \le 5 + \frac{7}{2} = \frac{{17}}{2}\forall x \in \mathbb{R}\end{array}\)
Dấu “=” xảy ra khi và chỉ khi \({x^2} = 0\) hay \(x = 0\).
Vậy giá trị lớn nhất của A là \(\frac{{17}}{2}\) khi x = 0.
* \(D = 4 - \left| {5x - 2} \right| - \left| {3y + 12} \right|\)
Ta có: \(D = 4 - \left| {5x - 2} \right| - \left| {3y + 12} \right| = 4 - \left( {\left| {5x - 2} \right| + \left| {3y + 12} \right|} \right)\) đạt giá trị lớn nhất khi và chỉ khi \(\left| {5x - 2} \right| + \left| {3y + 12} \right|\) nhỏ nhất.
Vì \(\left| {5x - 2} \right| \ge 0\,\forall x\) nên giá trị nhỏ nhất của \(\left| {5x - 2} \right| = 0\) khi \(x = \frac{2}{5}\);
\(\left| {3y + 12} \right| \ge 0\,\forall y \in \mathbb{R}\) nên giá trị nhỏ nhất của \(\left| {3y + 12} \right| = 0\) khi \(y = - 4\)
Vậy giá trị lớn nhất của D là \(D = 4 - \left( {0 + 0} \right) = 4\) khi \(x = \frac{2}{5}\), \(y = - 4\).
Bài 15*. Cho \(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}};B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\). So sánh A và B.
Phương pháp
Nhân cả hai vế của A và B với 2023 để so sánh.
Lời giải
Ta có:
\(\begin{array}{l}2023.A = \frac{{{{2023}^{2024}} + 2023}}{{{{2023}^{2024}} + 1}} = \frac{{\left( {{{2023}^{2024}} + 1} \right) + 2022}}{{{{2023}^{2024}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2024}} + 1}}\\2023.B = \frac{{{{2023}^{2023}} + 2023}}{{{{2023}^{2023}} + 1}} = \frac{{\left( {{{2023}^{2023}} + 1} \right) + 2022}}{{{{2023}^{2023}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\end{array}\)
Vì \({2023^{2024}} + 1 > {2023^{2023}} + 1\)
\(\begin{array}{l} \Rightarrow \frac{1}{{{{2023}^{2024}} + 1}} < \frac{1}{{{{2023}^{2023}} + 1}}\\ \Rightarrow \frac{{2022}}{{{{2023}^{2024}} + 1}} < \frac{{2022}}{{{{2023}^{2023}} + 1}}\\ \Rightarrow 1 + \frac{{2022}}{{{{2023}^{2024}} + 1}} < 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\\ \Rightarrow A < B\end{array}\)
Vậy A < B
-
Đề thi học kì 1 Toán 7 - Đề số 1 - Cánh diều
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
-
Đề thi học kì 1 Toán 7 - Đề số 2 - Cánh diều
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
-
Đề thi học kì 1 Toán 7 - Đề số 3 - Cánh diều
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
-
Đề thi học kì 1 Toán 7 - Đề số 4 - Cánh diều
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
-
Đề thi học kì 1 Toán 7 - Đề số 5 - Cánh diều
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.