Đề thi học kì 1 Toán 7 Cánh diều - Đề số 12Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Phần trắc nghiệm (3 điểm)Đề bài
I. Trắc nghiệm
Câu 1 :
Số đối của số \( - \frac{3}{5}\) là:
Câu 2 :
Căn bậc hai số học của 121 là:
Câu 3 :
Số nào là số vô tỉ trong các số sau:
Câu 4 :
Cho \(\left| x \right|\) = 16 thì giá trị của x là:
Câu 5 :
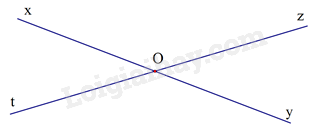
Cho hai đường thẳng xy và zt cắt nhau như hình vẽ, biết \(\widehat {xOz} = {140^0}\). Tính số đo \(\widehat {zOy}\):
Câu 6 :
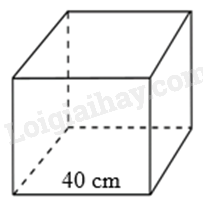
Cho hình lập phương có các kích thước như hình vẽ. Diện tích xung quanh của hình lập phương đó là:
Câu 7 :
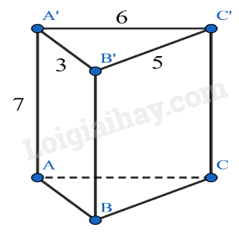
Cho hình lăng trụ đứng tam giác \(ABC.A'B'C'\) có cạnh \(A'B' = 3\,{\rm{cm}}\),\({B^\prime }{C^\prime } = 5\,{\rm{cm}}\), \(A'C' = 6\,{\rm{cm}}\), \(AA' = 7\:{\rm{cm}}\).
Diện tích xung quanh của hình lăng trụ đứng là:
Câu 8 :
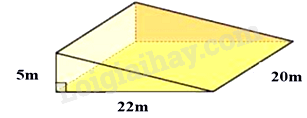
Nhà bạn An đang tiến hành làm một con dốc bằng bê tông để dẫn xe vào nhà có hình là một lăng trụ đứng tam giác có kích thước như hình dưới đây. Tính thể tích của con dốc.
Câu 9 :
Cho \(\widehat {xOy} = {120^0}\). Gọi Ot là tia phân giác của \(\widehat {xOy}\). Số đo\(\widehat {xOt}\) bằng:
Câu 10 :
Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau. Biết rằng x = 3 thì y = 15. Hệ số tỉ lệ nghịch là:
Câu 11 :
Cho tỉ lệ thức \(\frac{{15}}{x} = \frac{{ - 50}}{{20}}\). Giá trị của x là:
Câu 12 :
Cho biết x và y là hai đại lượng tỉ lệ thuận. Giá trị của a trong bảng là
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Số đối của số \( - \frac{3}{5}\) là:
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về số đối. Lời giải chi tiết :
Số đối của số \( - \frac{3}{5}\) là \(\frac{3}{5}\).
Câu 2 :
Căn bậc hai số học của 121 là:
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của số a không âm là số x không âm sao cho \({x^2} = a\). Lời giải chi tiết :
Căn bậc hai số học của 121 là \(\sqrt {121} = 11\).
Câu 3 :
Số nào là số vô tỉ trong các số sau:
Đáp án : B Phương pháp giải :
Số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn. Lời giải chi tiết :
Ta có: \(0 = \frac{0}{1};3,15 = \frac{{63}}{{20}}\). Các số \(\frac{4}{5};0;3,15\) là số hữu tỉ nên không phải là số vô tỉ.
Câu 4 :
Cho \(\left| x \right|\) = 16 thì giá trị của x là:
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về dấu giá trị tuyệt đối. \(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x \ge 0\\ - x\,khi\,x < 0\end{array} \right.\) Lời giải chi tiết :
\(\left| x \right|\) = 16 thì x = 16 hoặc x = – 16.
Câu 5 :
Cho hai đường thẳng xy và zt cắt nhau như hình vẽ, biết \(\widehat {xOz} = {140^0}\). Tính số đo \(\widehat {zOy}\):
Đáp án : C Phương pháp giải :
Dựa vào kiến thức hai góc kề bù. Lời giải chi tiết :
Vì \(\widehat {xOz}\) và \(\widehat {zOy}\) là hai góc kề bù nên \(\widehat {xOz} + \widehat {zOy} = {180^0}\) suy ra \(\widehat {zOy} = {180^0} - \widehat {xOz} = {180^0} - {140^0} = {40^0}\).
Câu 6 :
Cho hình lập phương có các kích thước như hình vẽ. Diện tích xung quanh của hình lập phương đó là:
Đáp án : A Phương pháp giải :
Dựa vào công thức tính diện tích xung quanh của hình lập phương: Sxq = 4.cạnh2. Lời giải chi tiết :
Diện tích xung quanh của hình lập phương này là: \({S_{xq}} = {4.40^2} = 6400\left( {c{m^2}} \right)\)
Câu 7 :
Cho hình lăng trụ đứng tam giác \(ABC.A'B'C'\) có cạnh \(A'B' = 3\,{\rm{cm}}\),\({B^\prime }{C^\prime } = 5\,{\rm{cm}}\), \(A'C' = 6\,{\rm{cm}}\), \(AA' = 7\:{\rm{cm}}\).
Diện tích xung quanh của hình lăng trụ đứng là:
Đáp án : A Phương pháp giải :
Dựa vào công thức tính diện tích xung quanh của hình lăng trụ đứng: Sxq = Cđáy. chiều cao. Lời giải chi tiết :
Diện tích xung quanh hình lăng trụ đứng đó là: \({S_{xq}} = \left( {3 + 5 + 6} \right).7 = 98\left( {c{m^2}} \right)\)
Câu 8 :
Nhà bạn An đang tiến hành làm một con dốc bằng bê tông để dẫn xe vào nhà có hình là một lăng trụ đứng tam giác có kích thước như hình dưới đây. Tính thể tích của con dốc.
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch. Lời giải chi tiết :
Vì x và y là hai đại lượng tỉ lệ nghịch với nhau nên hệ số tỉ lệ nghịch là: 3.15 = 45.
Câu 9 :
Cho \(\widehat {xOy} = {120^0}\). Gọi Ot là tia phân giác của \(\widehat {xOy}\). Số đo\(\widehat {xOt}\) bằng:
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về tia phân giác. Lời giải chi tiết :
Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}\widehat {xOy} = \frac{1}{2}{.120^0} = {60^0}\).
Câu 10 :
Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau. Biết rằng x = 3 thì y = 15. Hệ số tỉ lệ nghịch là:
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch. Lời giải chi tiết :
Vì x và y là hai đại lượng tỉ lệ nghịch với nhau nên hệ số tỉ lệ nghịch là: 3.15 = 45.
Câu 11 :
Cho tỉ lệ thức \(\frac{{15}}{x} = \frac{{ - 50}}{{20}}\). Giá trị của x là:
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về tỉ lệ thức: Nếu \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\). Lời giải chi tiết :
Ta có: \(\frac{{15}}{x} = \frac{{ - 50}}{{20}}\) suy ra \(15.20 = - 50.x \) Do đó \(x = \frac{{15.20}}{{ - 50}} = - 6\).
Câu 12 :
Cho biết x và y là hai đại lượng tỉ lệ thuận. Giá trị của a trong bảng là
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận: Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ k. Với mỗi giá trị x1 , x2 , x3 ,… khác 0 của x, lần lượt tương ứng với giá trị y1 , y2 , y3 ,… của y thì: \(\frac{y_1}{x_1} = \frac{y_2}{x_2} = \frac{y_3}{x_3} = .... = k\) Lời giải chi tiết :
Vì x và y là hai đại lượng tỉ lệ thuận nên \(\frac{{ - 3}}{6} = \frac{{ - 2}}{4} = \frac{1}{a} = \frac{2}{{ - 4}}\) hay \(\frac{1}{{ - 2}} = \frac{1}{a} \Rightarrow a = - 2\).
II. Tự luận
Phương pháp giải :
Sử dụng các quy tắc thực hiện phép tính. Lời giải chi tiết :
a) \(\frac{1}{3} - \frac{5}{4} + \frac{7}{6}\) \( = \frac{4}{{12}} - \frac{{15}}{{12}} + \frac{{14}}{{12}} = \frac{3}{{12}} = \frac{1}{4}\) b) \(\frac{{11}}{3} \cdot \frac{2}{5} + \frac{{11}}{3} \cdot \frac{8}{5} - \frac{{11}}{3}\) \( = \frac{{11}}{3} \cdot \left( {\frac{2}{5} + \frac{8}{5} - 1} \right) = \frac{{11}}{3} \cdot \left( {2 - 1} \right) = \frac{{11}}{3}\) Phương pháp giải :
- Sử dụng quy tắc chuyển vế. - Chia hai trường hợp để bỏ dấu giá trị tuyệt đối. Lời giải chi tiết :
Ta có: \(\frac{1}{3} - \left| {\frac{3}{4} - x} \right| = \frac{1}{{12}}\) \(\begin{array}{l}\left| {\frac{3}{4} - x} \right| = \frac{1}{3} - \frac{1}{{12}}\\\left| {\frac{3}{4} - x} \right| = \frac{1}{4}\end{array}\) \(\left| {\frac{3}{4} - x} \right| = \frac{1}{4}\) thì \(\frac{3}{4} - x = \frac{1}{4}\) hoặc \(\frac{3}{4} - x = - \frac{1}{4}\) TH1. \(\frac{3}{4} - x = \frac{1}{4}\) \(\begin{array}{l}x = \frac{3}{4} - \frac{1}{4}\\x = \frac{1}{2}\end{array}\) TH2. \(\frac{3}{4} - x = - \frac{1}{4}\) \(\begin{array}{l}x = \frac{3}{4} + \frac{1}{4}\\x = 1\end{array}\) Vậy \(x \in \left\{ {\frac{1}{2};1} \right\}\). Phương pháp giải :
Sử dụng phép chia sau đó làm tròn kết quả đến hàng phần trăm. Lời giải chi tiết :
Độ dài mỗi đoạn gỗ là: \(6,323 \div 4 = 1,58075 \approx 1,58\)(m) Vậy độ dài mỗi đoạn gỗ là khoảng 1,58m. Phương pháp giải :
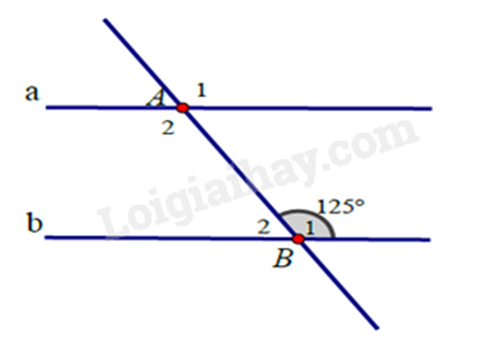
Dựa vào tính chất của hai đường thẳng song song. Lời giải chi tiết :
Vì a // b nên: \(\widehat {{A_1}} = \widehat {{B_1}} = {125^0}\) (hai góc đồng vị) Ta có: \(\widehat {{B_1}} + \widehat {{B_2}} = {180^0}\) (hai góc kề bù) Suy ra: \(\widehat {{B_2}} = {180^0} - \widehat {{B_1}} = {180^0} - {125^0} = {55^0}\). Phương pháp giải :
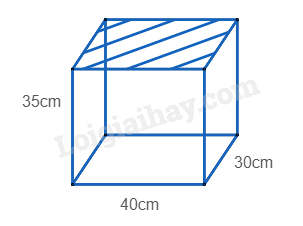
a) Tính diện tích xung quanh hình hộp chữ nhật + diện tích 1 đáy. b) Tính thể tích hình hộp chữ nhật đó. Lời giải chi tiết :
a) Diện tích kính làm hồ cá chính là diện tích xung quanh của hình hộp chữ nhật + diện tích một đáy của hình hộp chữ nhật. Vậy diện tích kính làm hồ cá là: 2.(40 + 30).35 + 40.30 = 6 100 (cm2). b) Số lít nước tối đa hồ cá có thể chứa được chính là thể tích của hình hộp chữ nhật. Vậy số lít nước tối đa hồ cá có thể chưa được là: 40.30.35 = 42 000 (cm3) = 42 (lít). Phương pháp giải :
Dựa vào cách làm tròn số với độ chính xác cho trước. Lời giải chi tiết :
Do độ chính xác (d = 500) đến hàng trăm nên ta làm tròn số 8 214 353 đến hàng nghìn và ta có: \(8{\rm{ 214 353}} \approx {\rm{ 8 214 000}}\) Phương pháp giải :
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch. Áp dụng tính chất của dãy tỉ số bằng nhau. Lời giải chi tiết :
Gọi x (máy), y (máy), z (máy) lần lượt là số máy cày của các đội 1, 2, 3 (điều kiện \(x,{\rm{ }}y,{\rm{ }}z \in N*\)) Vì diện tích các cánh đồng là như nhau nên số máy cày và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch, suy ra 3x = 5y = 6z. Đội thứ hai nhiều hơn đội thứ ba 1 máy nên y – z = 1. Từ 3x = 5y = 6z, suy ra \(\frac{x}{{\frac{1}{3}}} = \frac{y}{{\frac{1}{5}}} = \frac{z}{{\frac{1}{6}}}\) Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\frac{x}{{\frac{1}{3}}} = \frac{y}{{\frac{1}{5}}} = \frac{z}{{\frac{1}{6}}} = \frac{{y - z}}{{\frac{1}{5} - \frac{1}{6}}} = \frac{1}{{\frac{1}{{30}}}} = 30\) Do đó: \(\begin{array}{l}\frac{x}{{\frac{1}{3}}} = 30 \Rightarrow x = \frac{1}{3}.30 = 10\\\frac{y}{{\frac{1}{5}}} = 30 \Rightarrow \frac{1}{5}.30 = 6\\\frac{z}{{\frac{1}{6}}} = 30 \Rightarrow z = \frac{1}{6}.30 = 5\end{array}\) Vậy đội 1 có 10 máy cày, đội hai có 6 máy và đội 3 có 5 máy. Phương pháp giải :
Tính số tiền Minh phải trả sau khi giảm 5%. Tính số tiền Minh phải trả sau khi tính thẻ VIP. Lời giải chi tiết :
Vì Minh mua 1 cái áo giá 325 000 đồng và 1 đôi giày giá 490 000 đồng nên Minh sẽ phải trả tiền cho sản phẩm cao giá nhất đó là đôi giày giá 490 000 đồng. Số tiền Minh phải trả sau khi giảm giá 5% là: \(490\,000.\left( {100\% - 5\% } \right) = 465\;500\)(đồng). Số tiền Minh phải trả sau khi tính thẻ VIP là: \(465\;500.\left( {100\% - 10\% } \right) = 418\;950\)(đồng). Vậy số tiền Minh phải trả là 418 950 đồng.
|