Nội dung từ Loigiaihay.Com
Đề bài
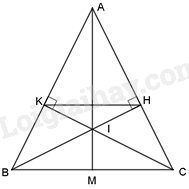
Cho tam giác ABC cân tại A. Kẻ \(BH \bot AC;CK \bot AB\) (\(H \in AC;\,\)\(K \in AB\)).
a) Chứng minh tam giác AKH là tam giác cân
b) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của \(\widehat {BIC}\).
c) Chứng minh: \(HK\,{\rm{//}}\,BC\).
Phương pháp giải :
a) Chứng minh \(\Delta ABH = \Delta ACK\) theo trường hợp cạnh huyền – góc nhọn. suy ra AH = AK nên tam giác AKH là tam giác cân.
b) Chứng minh \(\widehat {{P_1}} = \widehat {{N_1}}\) nên \(\Delta AKI = \Delta AHI\) theo trường hợp cạnh huyền – cạnh góc vuông suy ra \(\widehat {AIK} = \widehat {AIH}\)
Từ đó ta có \(\widehat {CIM} = \widehat {BIM}\) nên IM là phân giác của góc BIC
c) Từ tam giác cân ABC và AHK ta có \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\), \(\widehat {AKH} = \frac{{180^\circ - \widehat A}}{2}\) nên \(\widehat {ABC} = \widehat {AKH}\).
Mà hai góc này ở vị trí đồng vị nên HK // BC.
Lời giải chi tiết :
a) Xét \(\Delta ABH\) và \(\Delta ACK\) có:
\(\widehat {AHB} = \widehat {AKC} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\))
AB = AC (\(\Delta ABC\) cân);
góc A chung;
Do đó: \(\Delta ABH = \Delta ACK\) (cạnh huyền – góc nhọn).
\( \Rightarrow AH = AK \Rightarrow \Delta AHK\) cân tại A (đpcm).
b) Xét \(\Delta AKI\) và \(\Delta AHI\) có: \(\widehat {AKI} = \widehat {AHI} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\))
AK = AH (\(\Delta AHK\) cân tại A);
cạnh AI chung;
Do đó: \(\Delta AKI = \Delta AHI\) (cạnh huyền – cạnh góc vuông).
\( \Rightarrow \widehat {AIK} = \widehat {AIH}\).
Mà: \(\widehat {AIK} = \widehat {CIM};\widehat {AIH} = \widehat {BIM}\) (2 góc đối đỉnh).
Do đó: \(\widehat {CIM} = \widehat {BIM}\)\( \Rightarrow IM\)là phân giác của góc BIC (đpcm).
c) \(\Delta ABC\) cân tại A nên: \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\) .
\(\Delta AHK\) cân tại A nên: \(\widehat {AKH} = \frac{{180^\circ - \widehat A}}{2}\) .
Suy ra \(\widehat {ABC} = \widehat {AKH}\).
Mà 2 góc này ở vị trí đồng vị.
Do đó: KH // BC (đpcm).
Các bài tập cùng chuyên đề
Bài 1 :
a) Tính giá trị của biểu thức \(A = (2x + y)(2x - y)\) tại \(x = - 2,\;y = \frac{1}{3}.\)
b) Tìm tất cả các giá trị của \(x\) thoả mãn \(x(3x - 2) - 3{x^2} = \frac{3}{4}.\)
Bài 2 :
Học sinh của ba lớp 7A, 7B, 7C làm 40 tấm thiệp để chúc mừng các thầy cô nhân ngày 20-11, biết số học sinh của ba lớp 7A, 7B, 7C theo thứ tự là 45; 42; 33. Hỏi trong ba lớp trên mỗi lớp làm bao nhiêu tấm thiệp, biết số học sinh tỉ lệ với số thiệp cần làm.
Bài 3 :
Cho hai đa thức \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\) và \(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\)
a) Thu gọn hai đa thức \(A\left( x \right)\) và \(B\left( x \right)\) và sắp xếp theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) - B\left( x \right)\).
Bài 4 :
Tìm tất cả các số nguyên dương \(x,y,z\) thỏa mãn:
\(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\)và \(200 < {y^2} + {z^2} < 450\).
Bài 7 :
Trong các công thức sau, công thức nào phát biểu: “Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2”?
Bài 8 :
Biểu thức đại số biểu diễn công thức tính diện tích hình thang có 2 đáy độ dài a, b; chiều cao h ( a, b, h có cùng đơn vị đo độ dài)
Bài 10 :
Giá trị của đa thức \(g\left( x \right) = {x^8}{\rm{ + }}{x^4} + {x^2} + 1\) tại \(x = - 1\) bằng
Bài 12 :
Gieo một đồng xu cân đối, đồng chất 1 lần. Xác suất của biến cố “Đồng xu xuất hiện mặt ngửa” là
Bài 13 :
Cho \(\Delta ABC\) vuông tại A có \(\widehat B = {65^0}.\) Chọn khẳng định đúng.
Bài 14 :
Cho tam giác \(ABC\) có AM là đường trung tuyến, trọng tâm \(G\). Khẳng định nào sau đây đúng?