Đề thi học kì 1 Toán 7 Chân trời sáng tạo - Đề số 15Phần trắc nghiệm (3 điểm)Đề bài
I. Trắc nghiệm
Câu 1 :
Căn bậc hai số học của 16 là
Câu 2 :
Số nào là số vô tỉ trong các số sau:
Câu 3 :
Trong các số sau \( - 1\frac{2}{3};\,\,\,\frac{{ - 3}}{{ - 13}};\,\,\,\frac{0}{7};\,\,\,\frac{{ - 5}}{9};\,\,\,\frac{8}{{17}};\,\,0,23\) có bao nhiêu số hữu tỉ dương?
Câu 4 :
Kết quả của phép tính \(\sqrt {81} - 2\sqrt {16} \) là:
Câu 5 :
Cho \(\left| x \right|\) = 25 thì giá trị của x là:
Câu 6 :
Kết quả làm tròn số 17,8569 đến hàng phần trăm là:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Căn bậc hai số học của 16 là
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của số a không âm là số x không âm sao cho \({x^2} = a\). Lời giải chi tiết :
Căn bậc hai số học của 16 là \(\sqrt {16} = 4\).
Câu 2 :
Số nào là số vô tỉ trong các số sau:
Đáp án : A Phương pháp giải :
Số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn. Lời giải chi tiết :
Ta có: \(\sqrt {25} = 5\) là số hữu tỉ. – 5,(4561) là số thập phân vô hạn tuần hoàn. \(\frac{5}{3}\) là số hữu tỉ. Vậy chỉ có \(\sqrt 5 \) là số vô tỉ.
Câu 3 :
Trong các số sau \( - 1\frac{2}{3};\,\,\,\frac{{ - 3}}{{ - 13}};\,\,\,\frac{0}{7};\,\,\,\frac{{ - 5}}{9};\,\,\,\frac{8}{{17}};\,\,0,23\) có bao nhiêu số hữu tỉ dương?
Đáp án : C Phương pháp giải :
Số hữu tỉ dương là các số lớn hơn 0 có thể viết dưới dạng phân số. Lời giải chi tiết :
Ta có: \( - 1\frac{2}{3} < 0\); \(\frac{{ - 3}}{{ - 13}} = \frac{3}{{13}} > 0\); \(\frac{0}{7} = 0\); \(\frac{{ - 5}}{9} < 0\); \(\frac{8}{{17}} > 0\); \(0,23 = \frac{{23}}{{100}} > 0\). Vậy có 3 số hữu tỉ dương: \(\frac{{ - 3}}{{ - 13}};\frac{8}{{17}};0,23\).
Câu 4 :
Kết quả của phép tính \(\sqrt {81} - 2\sqrt {16} \) là:
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của số a không âm là số x không âm sao cho \({x^2} = a\). Lời giải chi tiết :
\(\sqrt {81} - 2\sqrt {16} = 9 - 2.4 = 9 - 8 = 1\).
Câu 5 :
Cho \(\left| x \right|\) = 25 thì giá trị của x là:
Đáp án : D Phương pháp giải :
Sử dụng định nghĩa giá trị tuyệt đối của một số: \(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x \ge 0\\ - x\,khi\,x < 0\end{array} \right.\). Lời giải chi tiết :
\(\left| x \right|\) = 25 thì x = 25 hoặc x = – 25.
Câu 6 :
Kết quả làm tròn số 17,8569 đến hàng phần trăm là:
Đáp án : C Phương pháp giải :
Dựa vào cách làm tròn số với độ chính xác cho trước. Lời giải chi tiết :
Do 6 > 5 \( \Rightarrow \) Làm tròn 17,8569 đến hàng phần trăm là : 17,8569 ≈ 17,86. Vậy làm tròn 17,8569 đến hàng phần trăm là 17,86.
Đáp án : B Phương pháp giải :
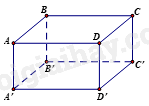
Dựa vào đặc điểm của hình hộp chữ nhật. Lời giải chi tiết :
Hình hộp chữ nhật ABCD.A’B’C’D’ có AB = A’B’ = CD = C’D’ = 5cm nên B đúng.
Đáp án : D Phương pháp giải :
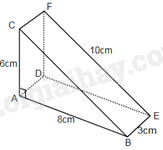
Dựa vào công thức tính thể tích của hình lăng trụ đứng: V = Sđáy.h. Lời giải chi tiết :
Khối gỗ hình lăng trụ đứng ABC.DEF có đáy là các tam giác vuông ABC và DEF. Diện tích đáy của khối gỗ là: S = \(\frac{1}{2}.6.8 = 24\)(cm2). Thể tích khối gỗ là: V = Sđáy.h = \(24.3 = 72\)(cm3).
Đáp án : D Phương pháp giải :
Dựa vào đặc điểm của hình lăng trụ đứng tam giác. Lời giải chi tiết :
Hình lăng trụ tam giác có hai đáy là hình tam giác nên chỉ có quyển lịch để bàn là hình lăng trụ đứng tam giác.
Đáp án : B Phương pháp giải :
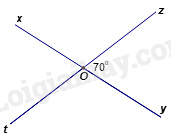
Dựa vào tính chất hai góc đối đỉnh. Lời giải chi tiết :
Ta có góc yOz và góc xOt là hai góc đối đỉnh nên \(\widehat {xOt} = \widehat {yOz} = {70^0}\).
Đáp án : C Phương pháp giải :
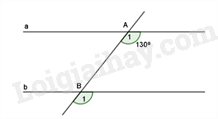
Dựa vào tính chất của hai đường thẳng song song. Lời giải chi tiết :
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}} = {130^0}\) (hai góc đồng vị).
Đáp án : D Phương pháp giải :
Dựa vào dấu hiệu nhận biết hai đường thẳng song song. Lời giải chi tiết :
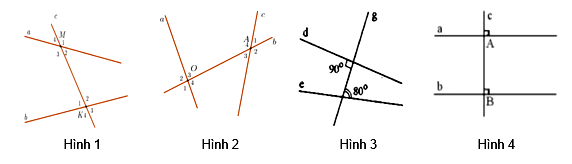
Hình 1 không có cặp góc nào bằng nhau nên không có hai đường thẳng song song. Hình 2 không có cặp góc nào bằng nhau nên không có hai đường thẳng song song. Hình 3 không có cặp góc nào bằng nhau nên không có hai đường thẳng song song. Hình 4 có cặp góc đồng vị bằng nhau (= 900) nên có hai đường thẳng song song.
II. Tự luận
Phương pháp giải :
a) Dựa vào thứ tự thực hiện để tính. b) Nhóm nhân tử chung để tính. Lời giải chi tiết :
a) \(\frac{5}{3} + \frac{{ - 7}}{{12}} + {\left( { - \frac{1}{2}} \right)^2}\)\( = \frac{5}{3} + \frac{{ - 7}}{{12}} + \frac{1}{4}\)\( = \frac{{13}}{{12}} + \frac{1}{4}\)\( = \frac{4}{3}\) b) \(\frac{{ - 17}}{{25}}.\frac{3}{{10}} + \frac{{ - 33}}{{25}}.\frac{3}{{10}} + \frac{3}{{10}}\)\( = \frac{3}{{10}}\left( {\frac{{ - 17}}{{25}} + \frac{{ - 33}}{{25}} + 1} \right)\)\( = \frac{3}{{10}}\left( { - 2 + 1} \right) = \frac{{ - 3}}{{10}}\) Phương pháp giải :
\(\left| x \right| = a\) khi và chỉ khi x = a hoặc x = -a. Lời giải chi tiết :
\(\left| {0,5x + \frac{3}{2}} \right| = \frac{3}{4}\) Suy ra \(0,5x + \frac{3}{2} = \frac{3}{4}\) hoặc \(0,5x + \frac{3}{2} = \frac{{ - 3}}{4}\) TH1. \(0,5x + \frac{3}{2} = \frac{3}{4}\) \(0,5x = \frac{3}{4} - \frac{3}{2}\) \(0,5x = \frac{{ - 3}}{4}\) \(x = \frac{{ - 3}}{2}\) TH2. \(0,5x + \frac{3}{2} = \frac{{ - 3}}{4}\) \(0,5x = \frac{{ - 3}}{4} - \frac{3}{2}\) \(0,5x = \frac{{ - 9}}{4}\) \(x = \frac{{ - 9}}{2}\) Vậy \(x \in \left\{ {\frac{{ - 3}}{2};\frac{{ - 9}}{2}} \right\}\). Phương pháp giải :
Tính giá bó hoa sau khi giảm 20%. Tính giá bó hoa khi mua từ bó thứ 10 trở đi. Tính tổng số tiền công ty phải trả khi mua 50 bó hoa = 9.giá bó hoa sau khi giảm 20% + 41.giá bó hoa khi mua từ bó thứ 10 trở đi. Lời giải chi tiết :
Sau khi giảm 20% thì giá 1 bó hoa bằng 100% - 20% = 80% giá bó hoa ban đầu. Giá 1 bó hoa sau khi giảm 20% là: 80 000.80% = 64 000 (đồng) Giá 1 bó hoa từ bó thứ 10 trở đi: 64 000.75% = 48 000 (đồng) Khi mua 50 bó hoa thì số bó hoa mua với giá 48 000 đồng là: 50 - 9 = 41 (bó) Vậy tổng số tiền công ty phải trả khi mua 50 bó hoa: 64 000.9 + 48 000.41 = 2 544 000 (đồng) Phương pháp giải :
Dựa vào công thức tính thể tích hình hộp chữ nhật: V = Sđáy.h. Số can nước = thể tích bể nước : dung tích can. Lời giải chi tiết :
Thể tích của bể nước là: V = 20.12.8 = 1920 (dm3) = 1920 lít Số can cần đổ để đầy bể nước là: 1920 : 20 = 96 (can). Vậy cần đổ 96 can nước để bể đầy nước. Phương pháp giải :
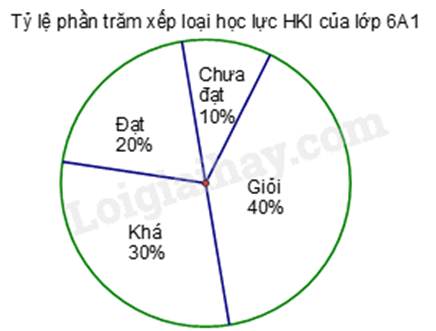
a) Xác định biểu đồ biểu diễn thông tin gì. Dựa vào biểu đồ để xác định số phần trăm mỗi đối tượng. b) Lấy tổng số học sinh nhân với số phần trăm học sinh giỏi và khá. Lời giải chi tiết :
a) Biểu đồ biểu diễn "Tỉ lệ phần trăm xếp loại học lực HKI của lớp 6A1". Bảng biểu diễn tỉ lệ % của mỗi đối tượng :
(Có thể lựa chọn vẽ bảng hoặc liệt kê phần trăm) b) Tổng số phần trăm học sinh giỏi và khá là : 40% + 30% = 70%. Số học sinh giỏi và khá của lớp 6A1 là : 50.70% = 35 (học sinh). Phương pháp giải :
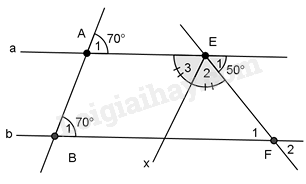
a) Chỉ ra 2 góc đồng vị bằng nhau b) Chứng minh hai góc so le trong bằng nhau và dựa vào tính chất hai góc kề bù. c) Dựa vào tính chất hai góc kề bù và tính chất tia phân giác. Lời giải chi tiết :
a) Ta có: \(\widehat {{A_1}} = \widehat {{B_1}}\). Mà hai góc này nằm ở vị trí so le trong nên a // b. b) Vì a // b nên \(\widehat {{E_1}} = \widehat {{F_1}} = {50^0}\)(2 góc so le trong). Mà \(\widehat {{F_1}}\) và \(\widehat {{F_2}}\) là hai góc đối đỉnh nên \(\widehat {{F_2}} = \widehat {{F_1}} = {50^0}\). c) Ta có góc E1 và góc AEF là hai góc kề bù nên \(\widehat {AEF} + \widehat {{E_1}} = {180^0}\) suy ra \(\widehat {AEF} = {180^0} - {50^0} = {130^0}\). Vì Ex là tia phân giác của góc AEF nên \(\widehat {{E_2}} = \widehat {{E_3}} = \frac{{\widehat {AEF}}}{2} = \frac{{{{130}^0}}}{2} = {65^0}\).
|