Đề thi học kì 1 Toán 7 Chân trời sáng tạo - Đề số 18Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Hai góc đối đỉnh thì
Câu 2 :
Số đối của \(\frac{{15}}{{16}}\) là
Câu 3 :
Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì
Câu 4 :
Căn bậc hai số học của 169 là:
Câu 5 :
Điểm kiểm tra học kì I (thang điểm 10) môn Toán của 4 bạn Mai, Hùng, Lan, Nhung được ghi lại trong bảng thống kê sau:
Trong bảng thống kê trên, số liệu nào không hợp lí?
Câu 6 :
Chọn khẳng định đúng:
Câu 7 :
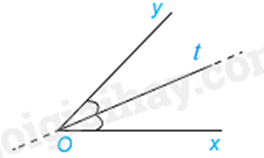
Cho \(\widehat {xOy} = 70^\circ \), tia Ot là tia phân giác của \(\widehat {xOy}\). Khi đó, số đo \(\widehat {xOt}\) bằng
Câu 9 :
Trong các số sau đây, số nào là số vô tỉ?
Câu 10 :
Phát biểu nào sau đây không đúng về hình lập phương?
Câu 11 :
Cho \(\left| x \right| = 4\) thì giá trị của x là:
Câu 12 :
Bạn An làm một chiếc hộp để đựng quà sinh nhật bằng bìa cứng có dạng hình hộp chữ nhật với chiều dài 25cm, chiều rộng 20cm, chiều cao 10cm. Thể tích của chiếc hộp là
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Hai góc đối đỉnh thì
Đáp án : C Phương pháp giải :
Dựa vào tính chất của hai góc đối đỉnh. Lời giải chi tiết :
Hai góc đối đỉnh thì bằng nhau. Đáp án C
Câu 2 :
Số đối của \(\frac{{15}}{{16}}\) là
Đáp án : B Phương pháp giải :
Hai số đối nhau thì có tổng bằng 1. Lời giải chi tiết :
Số đối của \(\frac{{15}}{{16}}\) là \( - \frac{{15}}{{16}}\) vì \(\frac{{15}}{{16}} + \left( { - \frac{{15}}{{16}}} \right) = 0\) Đáp án B
Câu 3 :
Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì
Đáp án : D Phương pháp giải :
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau. Lời giải chi tiết :
Nếu góc tạo thành có một cặp góc đồng vị bằng nhau thì a // b. Đáp án D
Câu 4 :
Căn bậc hai số học của 169 là:
Đáp án : B Phương pháp giải :
Áp dụng kiến thức về căn bậc hai của một số: \(x = {a^2}\) thì \(\sqrt x = a\). Lời giải chi tiết :
Căn bậc hai số học của 169 là \(\sqrt {169} = 13\). Đáp án B
Câu 5 :
Điểm kiểm tra học kì I (thang điểm 10) môn Toán của 4 bạn Mai, Hùng, Lan, Nhung được ghi lại trong bảng thống kê sau:
Trong bảng thống kê trên, số liệu nào không hợp lí?
Đáp án : A Phương pháp giải :
Dựa vào thang điểm để kiểm tra. Lời giải chi tiết :
Vì thang điểm của bài kiểm tra là 10 nên dữ liệu điểm của Lan là 10,5 là dữ liệu không hợp lí, vì điểm cao nhất có thể đạt được là 10 điểm. Đáp án A
Câu 6 :
Chọn khẳng định đúng:
Đáp án : C Phương pháp giải :
Kiểm tra xem các số có thuộc tập hợp số đó hay không. \({\mathbb{N}^*}\) là tập hợp số tự nhiên khác 0. \(\mathbb{N}\) là tập hợp số tự nhiên. \(\mathbb{Z}\) là tập hợp số nguyên. \(\mathbb{Q}\) là tập hợp số hữu tỉ. Lời giải chi tiết :
\(\sqrt 3 \) không phải là số tự nhiên nên \(\sqrt 3 \in \mathbb{N}\) là khẳng định sai. \(\sqrt 3 \) không phải là số nguyên nên \(\sqrt 3 \in \mathbb{Z}\) là khẳng định sai. \(\frac{2}{3}\) là số hữu tỉ nên \(\frac{2}{3} \in \mathbb{Q}\) là khẳng định đúng. \( - 9\) không phải là số tự nhiên nên \( - 9 \in {\mathbb{N}^*}\) là khẳng định sai. Đáp án C
Câu 7 :
Cho \(\widehat {xOy} = 70^\circ \), tia Ot là tia phân giác của \(\widehat {xOy}\). Khi đó, số đo \(\widehat {xOt}\) bằng
Đáp án : D Phương pháp giải :
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau. Lời giải chi tiết :
Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \frac{1}{2}.70^\circ = 35^\circ \). Đáp án D
Đáp án : A Phương pháp giải :
Tỉ lệ phần trăm sách khác = 100% - tỉ lệ phần trăm các loại sách đã biết. Lời giải chi tiết :
Tỉ lệ phần trăm của sách khác là: 100% - 20% - 30% - 35% = 15%. Đáp án A
Câu 9 :
Trong các số sau đây, số nào là số vô tỉ?
Đáp án : C Phương pháp giải :
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn. Lời giải chi tiết :
Số \(\sqrt {17} \) là số vô tỉ, các số còn lại là số hữu tỉ vì: \(\sqrt {25} = 5\); \(\sqrt {16} = 4\); \(\sqrt 9 = 3\). Đáp án C
Câu 10 :
Phát biểu nào sau đây không đúng về hình lập phương?
Đáp án : B Phương pháp giải :
Dựa vào đặc điểm của hình lập phương. Lời giải chi tiết :
Hình lập phương có: 6 mặt, 12 cạnh và 8 đỉnh nên A đúng, B sai. 4 đường chéo nên C đúng. các cạnh đều bằng nhau nên D đúng. Đáp án B
Câu 11 :
Cho \(\left| x \right| = 4\) thì giá trị của x là:
Đáp án : D Phương pháp giải :
Nếu \(\left| x \right| = a\) thì \(x = a\) hoặc \(x = - a\) Lời giải chi tiết :
Với \(\left| x \right| = 4\) thì \(x = 4\) hoặc \(x = - 4\). Đáp án D
Câu 12 :
Bạn An làm một chiếc hộp để đựng quà sinh nhật bằng bìa cứng có dạng hình hộp chữ nhật với chiều dài 25cm, chiều rộng 20cm, chiều cao 10cm. Thể tích của chiếc hộp là
Đáp án : A Phương pháp giải :
Thể tích của hình hộp chữ nhật là: V = chiều dài . chiều rộng . chiều cao. Lời giải chi tiết :
Thể tích của chiếc hộp là: \(V = 25.20.10 = 5000\left( {c{m^3}} \right)\) Đáp án A
II. Tự luận
Phương pháp giải :
Áp dụng thứ tự thực hiện phép tính: * Với các biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia, ta thực hiện các phép tính từ trái sang phải. * Với các biểu thức không có dấu ngoặc, ta thực hiện theo thứ tự: Lũy thừa => Nhân và chia => Cộng và trừ * Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau. Trường hợp có nhiều dấu ngoặc, ta thực hiện theo thứ tự ( ) => [ ] => { } Lời giải chi tiết :
a) \(\sqrt 9 + \left| { - 12} \right| = 3 + 12 = 15\) b) \(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^7}:{\left( {\frac{1}{3}} \right)^5} - 9\) \(\begin{array}{l} = \frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^{7 - 5}} - 9\\ = \frac{{17}}{9} + \frac{1}{9} - 9\\ = 2 - 9 = - 7\end{array}\) c) \(\left( {\frac{{ - 3}}{{17}} + \frac{5}{{13}}} \right) - \left( {\frac{{14}}{{17}} - \frac{8}{{13}}} \right)\) \(\begin{array}{l} = \frac{{ - 3}}{{17}} + \frac{5}{{13}} - \frac{{14}}{{17}} + \frac{8}{{13}}\\ = \left( {\frac{{ - 3}}{{17}} - \frac{{14}}{{17}}} \right) + \left( {\frac{5}{{13}} + \frac{8}{{13}}} \right)\\ = - 1 + 1 = 0\end{array}\) Phương pháp giải :
Áp dụng quy tắc chuyển vế đổi dấu. b) Đưa về dạng \(\left| A \right| = B\), chia hai trường hợp: A = B hoặc A = -B. Lời giải chi tiết :
a) \(5\frac{3}{4} + \frac{1}{4}:x = 5\frac{1}{2}\) \(\begin{array}{l}\frac{1}{4}:x = 5\frac{1}{2} - 5\frac{3}{4}\\\frac{1}{4}:x = \frac{1}{2} - \frac{3}{4}\\\frac{1}{4}:x = \frac{{ - 1}}{4}\\x = \frac{1}{4}:\frac{{ - 1}}{4}\\x = - 1\end{array}\) Vậy \(x = - 1\) b) \(\left| {x - \frac{3}{2}} \right| = \frac{7}{{12}}\) \(x - \frac{3}{2} = \frac{7}{{12}}\) hoặc \(x - \frac{3}{2} = - \frac{7}{{12}}\) \(x = \frac{7}{{12}} + \frac{3}{2}\) hoặc \(x = - \frac{7}{{12}} + \frac{3}{2}\) \(x = \frac{{25}}{{12}}\) hoặc \(x = \frac{{11}}{{12}}\) Vậy \(x \in \left\{ {\frac{{25}}{{12}};\frac{{11}}{{12}}} \right\}\) Phương pháp giải :
1. a) Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song với nhau. b) Áp dụng tính chất hai góc kề bù có tổng bằng \(180^\circ \) và hai đường thẳng song song thì hai góc đồng vị bằng nhau. 2. a) Áp dụng công thức tính thể tích hình lăng trụ đứng: V = diện tích đáy.chiều cao. b) Tính diện tích hai đáy, diện tích hai mặt bên được phủ bạt. Diện tích vải bạt bằng tổng diện tích hai đáy và diện tích hai mặt bên. Lời giải chi tiết :
1. a) Vì \(m \bot b,n \bot b\) nên \(m//n\). b) Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) (hai góc kề bù) nên \(\widehat {{B_3}} = 180^\circ - \widehat {{B_2}} = 180^\circ - 105^\circ = 75^\circ \). Vì m // n nên \(\widehat {{A_1}} = \widehat {{B_3}}\) (hai góc đồng vị) Mà \(\widehat {{B_3}} = 75^\circ \) nên \(\widehat {{A_1}} = 75^\circ \). 2. a) Thể tích của lều trại là: \(V = S.h = \frac{1}{2}.1,5.3,2.5 = 12\left( {c{m^3}} \right)\) b) Diện tích vải bạt cần phải có để dựng lều trại bằng tổng diện tích hai mặt đáy và diện tích hai mặt bên. Diện tích hai mặt đáy là: \(2.S = 2.\frac{1}{2}.1,5.3,2 = 4,8\left( {c{m^2}} \right)\) Diện tích hai mặt bên là: \(2.5.2,2 = 22\left( {c{m^2}} \right)\) Vậy diện tích vải bạt cần phải có để dựng lều trại là: \(4,8 + 22 = 26,8\left( {c{m^2}} \right)\) Phương pháp giải :
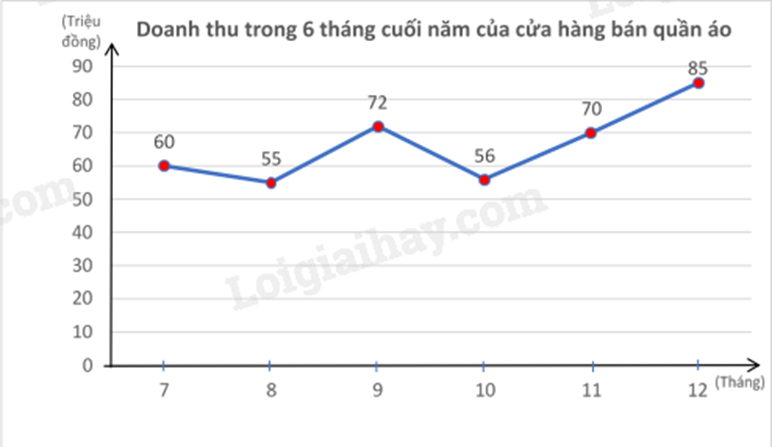
a) Cách vẽ biểu đồ đoạn thẳng: Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau - Trục ngang: Ghi các mốc thời gian - Trục dọc: Chọn khoảng chia thích hợp với số liệu và ghi số ở các vạch chia Bước 2: - Tại mỗi mốc thời gian trên trục ngang, đánh dấu một điểm cách điểm mốc thời gian theo chiều thẳng đứng một khoảng bằng số liệu tại mốc thời gian đó, tương ứng với khoảng chia trên trục dọc - Vẽ các đoạn thẳng nối từng cặp điểm tương ứng với cặp mốc thời gian liên tiếp, ta được một đường gấp khúc biểu diễn sự thay đổi số liệu theo thời gian. Bước 3: Hoàn thiện biểu đồ: - Ghi tên biểu đồ - Ghi chú các giá trị số liệu tại các đầu đoạn thẳng - Ghi đơn vị trên 2 trục b) Quan sát biểu đồ để xác định điểm biểu diễn tháng nào ở vị trí cao nhất, thấp nhất. Lời giải chi tiết :
a) Biểu đồ đoạn thẳng:
b) Tháng 12 cửa hàng có doanh thu cao nhất (85 triệu đồng). Tháng 8 cửa hàng có doanh thu thấp nhất (55 triệu đồng). Phương pháp giải :
a) Tính số tiền đôi giày được giảm. Số tiền bạn Nam phải trả = giá đôi giày – số tiền giảm. b) Tính giá tiền trước khi giảm 5% của khách hàng thân thiết. Tính giá ban đầu của cây vợt. Lời giải chi tiết :
a) Số tiền đôi giày được giảm là: 450 000 . 30% = 135 000 (đồng) Số tiền bạn Nam phải trả cho đôi giày là: 450 000 – 135 000 = 315 000 (đồng) b) Giá của cây vợt cầu lông trước khi được giảm giá thêm 5% là: 399 000 : (100% - 5%) = 420 000 (đồng) Giá ban đầu của cây vợt bạn Phúc đã mua là: 420000 : (100% - 30%) = 600 000 (đồng)
|