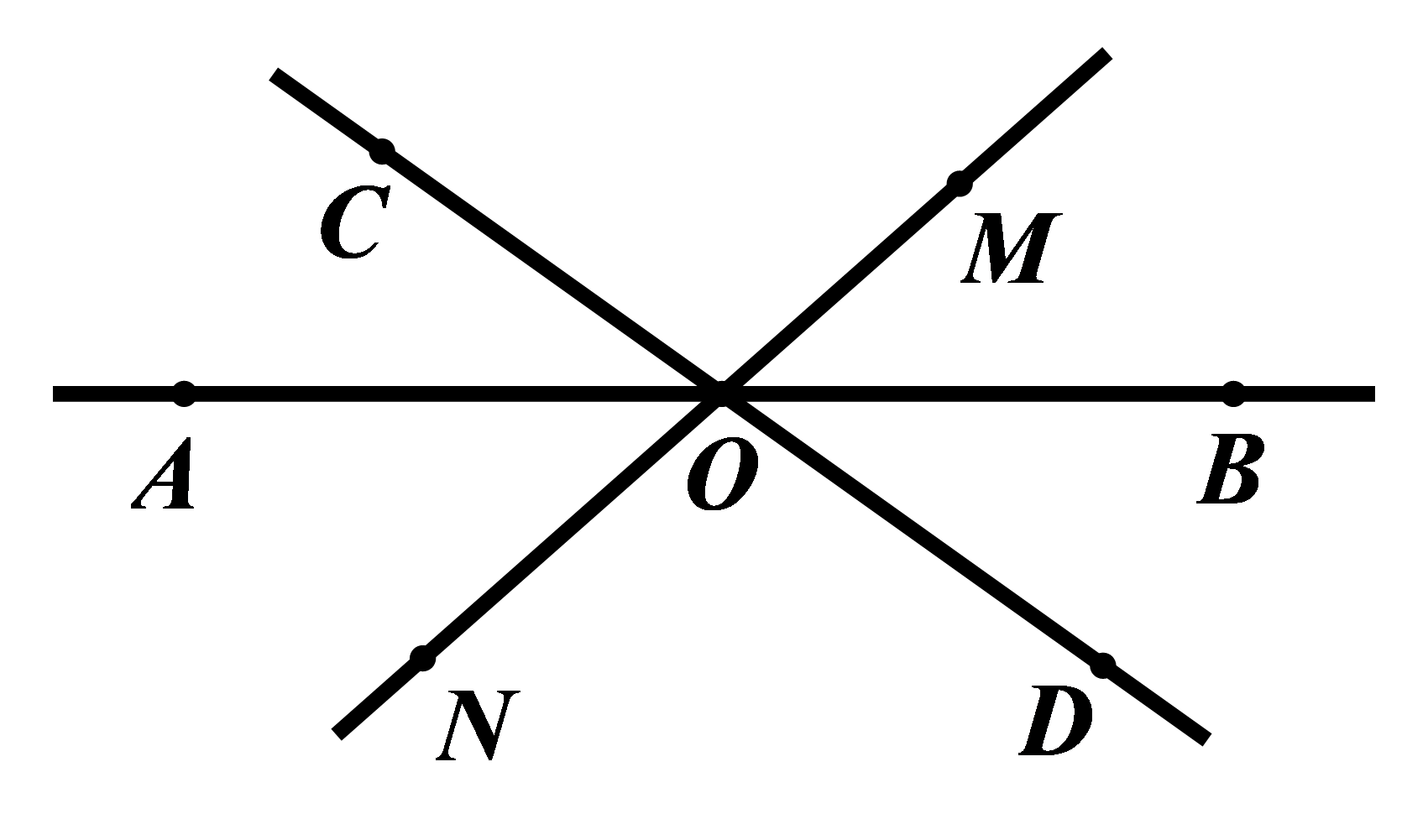Đề thi giữa kì 1 Toán 7 - Đề số 3Tải vềI. TRẮC NGHIỆM ( 3 điểm) Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
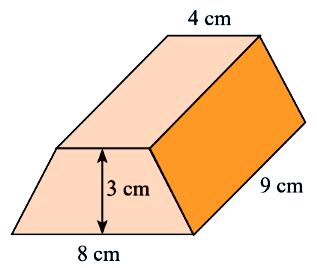
Đề bài I. TRẮC NGHIỆM ( 3 điểm) Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng. Câu 1: Điểm biểu diễn của số hữu tỉ −35 trên trục số là hình vẽ nào dưới đây? A. B. C. D. Câu 2: Kết quả của phép tính: −2,593−25 là: A. 2,993 B. −2,993 C. 2,193 D. −2,193 Câu 3: Trong các tập hợp sau, tập hợp nào có tất cả các phần tử đều là số vô tỉ? A. A={−0,1;√12;2132;−316} B. B={32,1;√25;√116;√0,01} C. C={√3;√5;√31;√83} D. D={−12;2312;25;−3} Câu 4: Hình hộp chữ nhật có ba kích thước: chiều dài là a, chiều rộng là b, chiều cao là c (a,b,c cùng đơn vị đo). Khi đó, diện tích xung quanh của hình hộp chữ nhật được tính theo công thức: A. Sxq=(a+b)c B. Sxq=2(a+b)c C. Sxq=(b+c)a D. Sxq=2(b+c)a Câu 5: Tính thể tích hình lăng trụ đứng có đáy là hình thang cân có kích thước như hình bên dưới: A. 72cm3 B. 162cm3 C. 88cm3 D. 132cm3 Câu 6: Hãy kể tên 4 góc kề với ∠AOC (không kể góc bẹt) trong hình vẽ dưới đây: A. ∠COM;∠MOB;∠AON;∠DOB B. ∠COM;∠COD;∠AON;∠MON C. ∠COM;∠COB;∠AON;∠AOD D. ∠COM;∠MOD;∠AON;∠CON Phần II. Tự luận (7 điểm): Bài 1: (1 điểm) Sắp xếp các số sau: a) Theo thứ tự tăng dần: −3,7;2111;112;−136;−15;37; b) Theo thứ tự giảm dần: −361;0;1748;215;2,45;−110. Bài 2: (2,0 điểm) Tính một cách hợp lí: a) −56.711+−511.46+56 b) [(−38+1123):59+(−58+1223):59].−11325 c) 15555−(−0,25)2.42 d) −215.9466.83+0,75.−12+0,375 Bài 3: (2,0 điểm) Tìm x, biết: a) (−0,4).(2x+25)=−9,4 b) (32−x):−143=−67 c) x+2.√16=−3.√49 d) 2+16−x=10.√0,01−√2536 Bài 4: (1,0 điểm) Một căn phòng có dạng hình hộp chữ nhật với chiều dài là 6m, chiều rộng là 4,2m, chiều cao là 3,2m. Người ta muốn sơn phía trong bốn bức tường và cả trần của căn phòng. Tính số tiền mà người ta phải trả, biết diện tích của các của của căn phòng là và giá tiền mỗi mét vuông (bao gồm tiền công và nguyên vật liệu) là 12 100 đồng. Bài 5: (1,0 điểm) Quan sát hình vẽ bên dưới, có ∠COD=800;∠COE=600, tia OG là tia phân giác của∠COD.
a) Tính số đo của ∠EOG? b) Tia OE có là tia phân giác của ∠DOG hay không? Giải thích vì sao? Lời giải I. TRẮC NGHIỆM ( 3 điểm)
Câu 1: Phương pháp: Biểu diễn số hữu tỉ trên trục số. Cách giải: Để biểu diễn số hữu tỉ −35 trên trục số, ta làm như sau: - Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành năm phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng 15 đơn vị cũ); - Đi theo chiều âm của trục số, bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm A. Điểm A biểu diễn số hữu tỉ −35. Chọn D. Câu 2: Phương pháp: Thực hiện phép trừ số hữu tỉ Cách giải: Ta có: −2,593−25=−2,593−0,4=−(2,593+0,4)=−2,993 Chọn B. Câu 3: Phương pháp: Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ. Loại trừ từng đáp án, chỉ ra một số trong tập hợp không là số vô tỉ, từ đó tìm được đáp án đúng. Cách giải: + Tâp hợp A={−0,1;√12;2132;−316} Ta có: −0,1 là hữu tỉ nên tập hợp A không thỏa mãn. + Tập hợp B={32,1;√25;√116;√0,01} Ta có: 32,1 là hữu tỉ nên tập hợp B không thỏa mãn. + Tập hợp {−12;2312;25;−3} Ta có: −12 là hữu tỉ nên tập hợp D không thỏa mãn. Chọn C. Câu 4: Phương pháp: Diện tích xung quanh của hình hộp chữ nhật có ba kích thước: chiều dài là a, chiều rộng là b, chiều cao là c (a,b,c cùng đơn vị đo) được tính theo công thức: Sxq=2(a+b)c Cách giải: Diện tích xung quanh của hình hộp chữ nhật có ba kích thước: chiều dài là a, chiều rộng là b, chiều cao là c (a,b,c cùng đơn vị đo) được tính theo công thức: Sxq=2(a+b)c Chọn B. Câu 5: Phương pháp: Diện tích hình thang có hai đáy bé và đáy lớn lần lượt là a,b và chiều cao h được tính theo công thức S=(a+b).h2 Thể tích hình lăng trụ có diện tích đáy là Sđáy và chiều cao h được tính theo công thức V=Sđáy .h Cách giải: Diện tích đáy của hình lăng trụ là: (4+8).32=18(cm2) Thể tích của hình lăng trụ là: V=18.9=162(cm3) Chọn B. Câu 6: Phương pháp: Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung. Cách giải: 4 góc kề với ∠AOC (không kể góc bẹt) trong hình vẽ là: ∠COM;∠COB;∠AON;∠AOD Chọn C.
Phần II. Tự luận Bài 1: Phương pháp: Đưa các số về dạng phân số có cùng mẫu số dương để so sánh. Cách giải: a) Theo thứ tự tăng dần: −3,7;2111;112;−136;−15;37; * So sánh các số: −3,7;−136;−15 Ta có: −3,7=−3710=−11130;−136=−6530;−15=−630 Vì −111<−65<−6 nên −11130<−6530<−630 suy ra −3,7<−136<−15 (1) * So sánh các số: 2111;112;37 Ta có: 2111=294154;112=32=231154;37=66154 Vì 66<231<294 nên 66254<231154<294154 suy ra 37<112<2111 (2) Từ (1) và (2), suy ra −3,7<−136<−15<37<112<2111 Vậy các số được sắp xếp theo thứ tự tăng dần là: −3,7;−136;−15;37;112;2111. b) Theo thứ tự giảm dần: −361;0;1748;215;2,45;−110. * So sánh các số: 1748;215;2,45 Ta có: 1748=85240;215=115=528240;2,45=245100=4920=588240 Vì 85<528<588 nên 85240<528240<588240 suy ra 1748<215<2,45 (1) * So sánh các số: −361;0;−110 Ta có: −361=−30610;0=0610;−110=−61610 Vì −61<−30<0 nên −61610<−30610<0610 nên −110<−361<0 (2) Từ (1) và (2) suy ra −110<−361<0<1748<215<2,45 Vậy các số được sắp xếp theo thứ tự giảm dần là: 2,45;215;1748;0;−361;−110. Bài 2: Phương pháp: a, b: Vận dụng tính chất phân phối của phép cộng và phép nhân: a.(b+d)=a.b+a.d c, d: Với hai số hữu tỉ x,y, ta có: (x.y)n=xn.yn;(xy)n=xnyn(y≠0) Cách giải: a) −56.711+−511.46+56 =56.(−711+−411+1)=56.(−1111+1)=56.(−1+1)=56.0=0 b) [(−38+1123):59+(−58+1223):59].−11325 =[(−38+1123).95+(−58+1223).95].−11325=[95.(−38+1123+−58+1223)].−11325=[95.(−88+2323)].−11325=95.(−1+1).−11325=95.0.−11325=0 c) 15555−(−0,25)2.42 =(155)5−(−0,25.4)2=35−(−1)2=243−1=242 d) −215.9466.83+0,75.−12+0,375 =−215.(32)4(2.3)6.(23)3+(−0,375)+0,375=−215.3826.36.29+[(−0,375)+0,375]=−215.38215.36+0=−32=9
Bài 3: Phương pháp: Vận dụng quy tắc chuyển vế để tìm x. Cách giải: a) (−0,4).(2x+25)=−9,4 2x+25=−9,4:(−0,4)2x+25=−9410:(−4)102x+25=−9410.10(−4)2x+25=4722x=472−25 2x=23510−4102x=23110x=23110:2x=23120 Vậy x=23120 b) (32−x):−143=−67 32−x=−67.(−14)332−x=4x=32−4x=32−82x=−52 Vậy x=−52 c) x+2.√16=−3.√49 x+2.√42=−2√72x+2.4=−2.7x+8=−14x=−14−8x=−22 Vậy x=−22 d) 2+16−x=10.√0,01−√2536 126+16−x=10.√(0,1)2−√5262136−x=10.0,1−56136−x=1−56=66−56136−x=16x=136−16x=126x=2 Vậy x=2 Bài 4: Phương pháp: Diện tích xung quanh của căn phòng theo công thức tính diên tích xung quanh của hình hộp chữ nhật có ba kích thước: chiều dài là a, chiều rộng là b, chiều cao là c (a,b,c cùng đơn vị đo) được tính theo công thức: Sxq=2(a+b)c (1) Diện tích trần của căn phòng được tính theo công thức diện tích hình chữ nhật có chiều rộng là a, chiều dài là b thì S=ab (2) Diện tích cần quét sơn = (1) + (2) – diện tích các của sổ Số tiền phải chi trả = diện tích cần quét sơn . giá tiền 1m2 Cách giải: Diện tích xung quanh của căn phòng là: 2.(6+4,2).3,2=65,28(m2) Diện tích trần của căn phòng là: 6.4,2=25,2(m2) Diện tích cần quét sơn của căn phòng là: 65,28+25,2−8,48=82(m2) Số tiền người đó cần phải trả để quét sơn căn phòng là: 82.12100=992200 (đồng) Bài 5: Phương pháp: Vận dụng kiến thức tia phân giác của một góc; hai góc kề nhau. Cách giải: a) Vì OG là tia phân giác của ∠COD nên ∠COG=∠DOG=12∠COD=12.800=400 (tính chất tia phân giác của một góc) Vì hai góc ∠COG và ∠EOG là hai góc kề nhau nên ∠COG+∠EOG=∠COE Suy ra 400+∠EOG=600 ⇒∠EOG=600−400=200 Vậy ∠EOG=200 b) Vì hai góc ∠COE và ∠DOE là hai góc kề nhau nên ∠COE+∠DOE=∠COD Suy ra 600+∠DOE=800 ⇒∠DOE=800−600=200 Do đó, ∠EOG=∠DOE=200 Mặt khác OE nằm giữa hai tia OD và OG nên OE là tia phân giác của ∠DOG.
|