Đề thi học kì 1 Toán 7 - Đề số 5 - Chân trời sáng tạoTải vềPhần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Cách viết nào dưới đây không đúng? A. √49=7 B. −√49=−7 C. √49=±7 D. √(−7)2=7 Câu 2: (−3)4 có giá trị bằng: A. -81 B. 12 C. 81 D. -12 Câu 3: Một cửa hàng bán nước hoa quả đã khảo sát về các loại nước mà khách hàng ưa chuộng và thu được bảng dữ liệu sau:
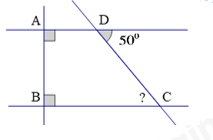
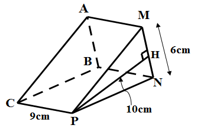
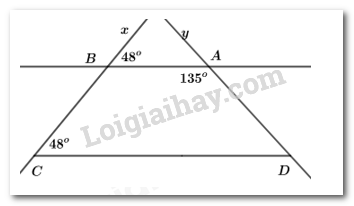
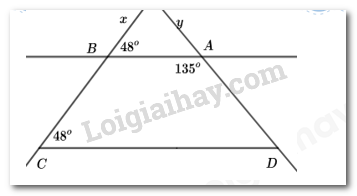
Loại nước nào ít người ưa chuộng nhất? A. Nước cam B. Nước dứa C. Nước chanh D. Nước ổi Câu 4: Trong các phân số sau, phân số nào biểu diễn số hữu tỉ −0,75? A. −62 B. 8−6 C. 9−12 D. −129 Câu 5: Nếu góc xOy có số đo bằng 470 thì số đo của góc đối đỉnh với góc xOy bằng bao nhiêu? A. 74 B. 47 C. 43 D. 133 Câu 6: Làm tròn số 1,7846 đến hàng phần nghìn ta được số nào A. 1,78 B. 1,8 C. 1,784 D. 1,785 Câu 7: Cho |a|=25 thì: A. a=25 B. a=−25 C. a=25 hoặc a=−25 D. a=25 hoặc a = 1 Câu 8: Cho hình vẽ. Số đo của góc ∠DCB trong hình vẽ bên là: A. 40 B. 50 C. 90 D. 140 Câu 9: Nếu a⊥b và b//c thì: A. a∥b B. a⊥c C. b⊥c D. a∥b∥c Câu 10: Tính thể tích của khối lăng trụ đứng ABC. MNP ở hình vẽ sau, trong đó PC = 9cm, MN = 6cm, PH = 10cm. A. 30 B. 270 C. 540 D. 135 Phần II: Tự luận (7 điểm). Câu 1: (2 điểm) Thực hiện phép tính sau: a. 917+89:179 b. (23)2+|(−213)|−√4964 c. (1511−413):1217+(711−913):1217 d. 203.(−49)2143.54 Câu 2: (1,5 điểm) Tìm x a. 132−x=53 b. x:43=214:13 c. |x−12|−√25=−2 Câu 3: (1,5 điểm) Cho hình vẽ, biết ∠xBA=48o,∠BCD=48o,∠BAD=135o. a) Chứng minh AB//CD. b) Hãy tính số đo góc ∠ADC. Câu 4: (1,5 điểm) Một bể bơi có chiều dài 12m, chiều rộng 5m và sâu 2,75m. Hỏi người thợ phải dung bao nhiêu viên gạch men hình chữ nhật để lát đáy và xung quanh thành bể đó? Biết rằng diện tích mạch vữa lát không đáng kể và mỗi viên gạch có chiều dài 25cm, chiều rộng 20cm. Câu 5: (0,5 điểm) Tìm x biết: |2x−1|+|1−2x|=8 Lời giải I. Phần trắc nghiệm (3 điểm)
Câu 1 Phương pháp: Giá trị của căn bậc hai số học là 1 số không âm. Cách giải: √49=±7là sai. Chọn C. Câu 2 Phương pháp: (−3)4=(-3) (-3) (-3) (-3) Cách giải: (−3)4=81 Chọn C. Câu 3 Phương pháp: Đọc và miêu tả dữ liệu từ bảng thống kê. Cách giải: Loại nước ít người ưa chuộng nhất là nước dứa. Chọn B. Câu 4 Phương pháp: Rút gọn từng phân số Cách giải: Ta có: −0,75=−75100=(−75):25100:25=−34 9−12=3.3−4.3=−34 Chọn C. Câu 5 Phương pháp: Hai góc đối đỉnh có số đo bằng nhau. Cách giải: Hai góc đối đỉnh có số đo bằng nhau nên ^xOy=47∘. Chọn B. Câu 6 Phương pháp: Hàng phần nghìn là số 4 có hàng phần chục nghìn là số 6 lớn hơn 5 Cách giải: Hàng phần nghìn là số 4 có hàng phần chục nghìn là số 6 lớn hơn 5 nên ta làm tròn thành 1,785 Chọn D. Câu 7 Phương pháp: |25|=25 và |−25|=25 Cách giải: |a|=25 suy ra a=25 hoặc a=−25 Chọn C. Câu 8 Phương pháp: ∠DCBvà góc ∠D là 2 góc so le trong Cách giải: ∠DCBvà góc ∠D là 2 góc so le trong nên ∠DCB=500 Chọn B. Câu 9 Phương pháp: Từ vuông góc đến song song. Cách giải: b∥c mà a⊥b nên a⊥c Chọn B. Câu 10 Phương pháp: Thể tích của khối lăng trụ đứng bằng chiều cao nhân diện tích đáy. Cách giải: Hình lăng trụ đứng tam giác ABC.MNP có chiều cao là CP=9cm. Chọn B. II. Phần tự luận (7 điểm) Câu 1 Phương pháp: Thực hiện phép tính theo thứ tự thực hiện phép tính. Cách giải: a. 917+89:179=917+89.917=917+817=1717=1 b. (23)2+|(−213)|−√4964=49+73−78=32+168−6372=13772 c. (1511−413):1217+(711−913):1217=1712.(1511−413+711−913)=1712.(2211−1313)=1712.(2−1)=1712 d. 203.(−49)2143.54=(26.53).(74)(23.73).54=23.75=565 Câu 2 Phương pháp: |x|=a với (a>0)⇔[x=ax=−a x2=avới (a>0) ⇔[x=√ax=−√a Cách giải: a. 132−x=53⇒x=52−53⇒x=56 b.x:43=214:13⇒x=94.31.43⇒x=9 c.|x−12|−√25=−2⇒[x−12=3x−12=−3⇒[x=72x=−52 Câu 3 Phương pháp: - Nếu một đường thẳng cắt hai đường thẳng song song thì: + Hai góc so le trong bằng nhau; + Hai góc đồng vị bằng nhau. - Dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt đường thẳng phân biệt ab, và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng hai thì a và b song song với nhau. Cách giải: a) Ta có ∠xBA=48o,∠BCD=48o(gt) ⇒∠xBA=∠BCD(=48o) Mà hai góc trên ở vị trí đồng vị ⇒AB//CD(dhnb) b) Vì AB//CD(cmt)⇒∠yAB=∠ADC (hai góc đồng vị) Ta lại có: ∠yAB+∠BAD=180o (hai góc kề bù) ∠yAB+135o=180o⇒∠yAB=180o−135o=45o ⇒∠ADC=∠yAB=45o. Câu 4 Phương pháp: Tính diện tích xung quanh bể bơi, diện tích đáy bể, diện tích cần lát gạch, diện tích 1 viên gạch. Từ đó tính số viên gạch cần lát. Cách giải: Diện tích xung quanh của bể bơi là: 2.(12+5).2,75=93,5(m2) Diện tích đáy bể bơi là: 12.5=60(m2) Diện tích cần lát gạch là: 93,5+60=153,5(m2)=1535000(m2) Diện tích một viên gạch lát là: 25.20=500(cm2) Số viên gạch cần để lát bể bơi là: 1535000:500=3070(viên gạch) Câu 5 Phương pháp: Dùng đẳng thức |a|=|−a|. Cách giải: Vì 2x – 1 và 1 – 2x là hai số đối nhau, nên: |2x−1|=|1−2x| Từ (1) và (2) suy ra: 2|2x−1|=8⇔|2x−1|=4⇔[2x−1=42x−1=−4⇔[x=52x=−32 Vậy x∈{52;−32}.
|