Đề cương ôn tập học kì 2 Toán 7 - Chân trời sáng tạoTải vềA. NỘI DUNG ÔN TẬP Đại số 1. Các đại lượng tỉ lệ - Tỉ lệ thức – Dãy tỉ số bằng nhau - Đại lượng tỉ lệ thuận - Đại lượng tỉ lệ nghịch 2. Biểu thức đại số - Biểu thức số và biểu thức đại số - Đa thức một biến - Phép tính với đa thức một biến (Phép cộng và phép trừ, Phép nhân và phép chia) Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên... A. NỘI DUNG ÔN TẬP Đại số 1. Các đại lượng tỉ lệ 2. Biểu thức đại số Hình học Xác suất B. BÀI TẬP Đề bài I. Phần trắc nghiệm II. Phần tự luận Lời giải chi tiết I. Phần trắc nghiệm II. Phần tự luận A. NỘI DUNG ÔN TẬPĐại số1. Các đại lượng tỉ lệ- Tỉ lệ thức – Dãy tỉ số bằng nhau 2. Biểu thức đại số- Biểu thức số và biểu thức đại số - Đa thức một biến - Phép tính với đa thức một biến (Phép cộng và phép trừ, Phép nhân và phép chia) Hình học- Góc và cạnh của một tam giác - Tam giác bằng nhau - Tam giác cân - Đường vuông góc và đường xiên - Đường trung trực của một đoạn thẳng - Tính chất ba đường trung trực của tam giác - Tính chất ba đường trung tuyến của tam giác - Tính chất ba đường cao của tam giác - Tính chất ba đường phân giác của tam giác Xác suất- Làm quen với biến cố ngẫu nhiên - Làm quen với xác suất của biến cố ngẫu nhiên
|
|
Câu 1. A |
Câu 2. C |
Câu 3. D |
Câu 4. B |
Câu 5. C |
|
Câu 6. A |
Câu 7. D |
Câu 8. B |
Câu 9. D |
Câu 10. D |
|
Câu 11. C |
Câu 12. D |
Câu 13. D |
Câu 14. B |
Câu 15. B |
|
Câu 16. B |
Câu 17. D |
Câu 18. C |
Câu 19. A |
Câu 20. A |
|
Câu 21. A |
Câu 22. D |
Câu 23. C |
Câu 24. D |
Câu 25. D |
|
Câu 26. C |
Câu 27. A |
Câu 28. C |
Câu 29. B |
Câu 30. D |
|
Câu 31. B |
Câu 32. C |
Câu 33. B |
Câu 34. B |
Câu 35. A |
II. Phần tự luận
Bài 1. Cho \(A\left( x \right) = 2{x^4} + 4{x^3} - 3{x^2} - 4x + 1\).
a) Xác định bậc, hạng tử tự do, hạng tử cao nhất của đa thức.
b) Tìm B(x) biết \(A\left( x \right) + B\left( x \right) = 2{{\rm{x}}^3} - {x^2} + 5\)
c) Tính \(A\left( x \right):\left( {{x^2} - 1} \right)\).
Phương pháp
a) Dựa vào kiến thức về bậc, hạng tử tự do, hạng tử cao nhất để trả lời.
b) Áp dụng quy tắc cộng, trừ đa thức một biến để tìm B(x).
c) Áp dụng quy tắc chia đa thức cho đa thức để tính.
Lời giải
a) Bậc của đa thức là 4.
Hạng tử tự do là 1.
Hạng tử cao nhất của đa thức là 2.
b) Ta có: \(A\left( x \right) + B\left( x \right) = 2{{\rm{x}}^3} - {x^2} + 5\)
\(\begin{array}{l}B\left( x \right) = \left( {2{{\rm{x}}^3} - {x^2} + 5} \right) - A\left( x \right)\\ = \left( {2{{\rm{x}}^3} - {x^2} + 5} \right) - \left( {2{x^4} + 4{x^3} - 3{x^2} - 4x + 1} \right)\\ = 2{x^3} - {x^2} + 5 - 2{x^4} - 4{x^3} + 3{x^2} + 4x - 1\\ = - 2{x^4} + \left( {2{x^3} - 4{x^3}} \right) + \left( { - {x^2} + 3{x^2}} \right) + 4x + \left( {5 - 1} \right)\\ = - 2{x^4} - 2{x^3} + 2{x^2} + 4x + 4\end{array}\)
Vậy \(B\left( x \right) = - 2{x^4} - 2{x^3} + 2{x^2} + 4x + 4\)
c) Ta có:
\(A\left( x \right):\left( {{x^2} - 1} \right) = \left( {2{x^4} + 4{x^3} - 3{x^2} - 4x + 1} \right):\left( {{x^2} - 1} \right)\)

Vậy \(A\left( x \right):\left( {{x^2} - 1} \right) = 2{x^2} + 4x - 1\)
Bài 2. Cho \(A\left( x \right) = 4{x^2} + 4x + 1\).
a) Xác định bậc, hạng tử tự do, hạng tử cao nhất của đa thức.
b) Tìm B(x) biết \(A\left( x \right) + B\left( x \right) = 5{x^2} + 5x + 1\).
c) Tính \(A\left( x \right):\left( {2{x^{}} + 1} \right)\).
Phương pháp
a) Dựa vào kiến thức về bậc, hạng tử tự do, hạng tử cao nhất để trả lời.
b) Áp dụng quy tắc cộng, trừ đa thức một biến để tìm B(x).
c) Áp dụng quy tắc chia đa thức để tính.
Lời giải
a) Bậc của đa thức là 2.
Hạng tử tự do là 1.
Hạng tử cao nhất của đa thức là 4.
b) Ta có: \(A\left( x \right) + B\left( x \right) = 5{x^2} + 5x + 1\)
\(\begin{array}{l}B\left( x \right) = \left( {5{x^2} + 5x + 1} \right) - \left( {4{x^2} + 4x + 1} \right)\\ = 5{x^2} + 5x + 1 - 4{x^2} - 4x - 1\\ = \left( {5{x^2} - 4{x^2}} \right) + \left( {5x - 4x} \right) + \left( {1 - 1} \right)\\ = {x^2} + x\end{array}\)
Vậy \(B\left( x \right){\rm{ }} = {x^2} + x\)
c) Ta có: \(A\left( x \right):\left( {2x + 1} \right) = \left( {4{x^2} + 4x + 1} \right):\left( {2x + 1} \right)\)
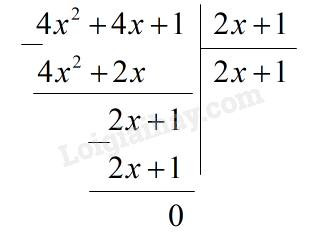
Vậy \(A\left( x \right):\left( {2x + 1} \right) = 2x + 1\)
Bài 3. Tìm x trong các tỉ lệ thức sau:
a) x : 27 = –2 : 3,6
b) \(\frac{{2x + 1}}{{-27}} = \frac{{- 3}}{{2x + 1}}\)
Phương pháp
Dựa vào kiến thức về tỉ lệ thức:
+ Nếu \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\).
+ Nếu \(ad = bc\) (với \(a,b,c,d \ne 0\)) thì ta có các tỉ lệ thức:
\(\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{b}{a} = \frac{d}{c};\frac{c}{a} = \frac{d}{b}\).
Lời giải
a) \(x:27 = -2:3,6\)
\(\begin{array}{l}\frac{x}{{27}} = \frac{{- 5}}{9}\\x = \frac{{- 5.27}}{9}\\x = -15\end{array}\)
Vậy \(x = -15\).
b) \(\frac{{2x + 1}}{{-27}} = \frac{{- 3}}{{2x + 1}}\)
\(\begin{array}{l}{\left( {2x + 1} \right)^2} = 81\\{\left( {2x + 1} \right)^2} = {9^2}\\\left[ \begin{array}{l}2x + 1 = 9\\2x + 1 = -9\end{array} \right.\\\left[ \begin{array}{l}2x = 8\\2x = -10\end{array} \right.\\\left[ \begin{array}{l}x = 4\\x = -5\end{array} \right.\end{array}\)
Vậy \(x = 4\) hoặc \(x = - 5\).
Bài 4. Biết \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch với nhau được liên hệ theo công thức \(y = - \frac{{16}}{x}\)
a) Tìm hệ số \(a?\)
b) Tính \(y\) khi \(x = - 4;x = 8.\)
Phương pháp
a) Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch.
b) Thay x vào công thức để tìm y.
Lời giải
a) Ta có: \(y = - \frac{{16}}{x}\) hay \(xy = - 16\) nên hệ số a là -16.
b) Thay x = -4 vào công thức \(y = - \frac{{16}}{x}\) ta được: \(y = - \frac{{16}}{{ - 4}} = 4\)
Thay x = 8 vào công thức \(y = - \frac{{16}}{x}\) ta được: \(y = - \frac{{16}}{8} = - 2\)
Vậy \(y = 4\) khi \(x = - 4;\) \(y = - 2\) khi \(x = 8.\)
Bài 5. Để hưởng ứng phong trào làm xanh môi trường học tập, học sinh lớp 7 cần phải trồng và chăm sóc 40 cây xanh. Lớp 7A có 36 học sinh, lớp 7B có 45 học sinh, lớp 7C có 39 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao nhiêu cây xanh, biết rằng số cây xanh tỉ lệ với số học sinh.
Phương pháp
Gọi số cây xanh mà mỗi lớp phải trồng và chăm sóc lần lượt là \(x;y;z\left( {x;y;z \in \mathbb{N}*,x;y;z < 40} \right)\)
Viết phương trình dựa vào đề bài.
Áp dụng tính chất dãy tỉ số bằng nhau để tìm x, y, z.
Lời giải
Gọi số cây xanh mà mỗi lớp phải trồng và chăm sóc lần lượt là \(x;y;z\left( {x;y;z \in \mathbb{N}*,x;y;z < 40} \right)\)
Vì số cây phải trồng và chăm sóc là 40 nên \(x + y + z = 40\)
Vì số cây xanh tỉ lệ với số học sinh nên ta có: \(\frac{x}{{36}} = \frac{y}{{45}} = \frac{z}{{39}}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{{36}} = \frac{y}{{45}} = \frac{z}{{39}} = \frac{{x + y + z}}{{36 + 45 + 39}} = \frac{{40}}{{120}} = \frac{1}{3}\)
Từ đó ta tính được \(\left( {x,y,z} \right) = \left( {12;15;13} \right)\).
Vậy số cây ba lớp 7A, 7B, 7C phải trồng và chăm sóc lần lượt là 12; 15; 13.
Bài 6. Để ủng hộ các bạn vùng bão lũ Miền Trung học sinh ba lớp 7A, 7B, 7C của trường THCS A tham gia ủng hộ vở viết. Biết rằng số vở viết ủng hộ được của mỗi lớp lần lượt tỉ lệ với các số 2; 3; 4 và tổng số vở viết ủng hộ được của ba lớp là 360 . Hỏi mỗi lớp ủng hộ được bao nhiêu quyển vở?
Phương pháp
Gọi số quyển vở ba lớp ủng hộ được lần lượt là a,b,c ( \(a,b,c \in N*\)).
Viết các biểu thức theo a, b, c.
Áp dụng tính chất dãy tỉ số bằng nhau để tìm a, b, c.
Lời giải
Gọi số quyển vở ba lớp ủng hộ được lần lượt là a,b,c ( \(a,b,c \in N*\)).
Theo đề bài ta có: \(\frac{a}{2} = \frac{b}{3} = \frac{c}{4}\) và \(a + b + c = 360\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{2} = \frac{b}{3} = \frac{c}{4}{\rm{ = }}\frac{{a + b + c}}{9} = \frac{{360}}{9} = 40\)
\( \Rightarrow \left\{ \begin{array}{l}\\\\\end{array} \right.\)\(\begin{array}{*{20}{l}}{a{\rm{ }} = 40.2{\rm{ }} = {\rm{ }}80}\\{b{\rm{ }} = {\rm{ 40}}.3{\rm{ }} = {\rm{ 120}}}\\{c{\rm{ }} = {\rm{ 40}}.4{\rm{ }} = {\rm{ 160}}}\end{array}\)
Vậy số quyển vở ba lớp 7A, 7B, 7C ủng hộ được lần lượt là 80, 120, 160.
Bài 7. Lan và Hoa mỗi người gieo một con xúc xắc.
a) Biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc là một số lớn hơn 1” là biến cố gì?
b) Biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7” là biến cố gì?
Phương pháp
Xác định số kết quả xảy ra của biến cố đó, ta xác định được biến cố đó là biến cố gì.
+) Biến cố chắc chắn: là biến cố biết trước được luôn xảy ra.
+) Biến cố không thể: là biến cố biết trước được không bao giờ xảy ra.
+) Biến cố ngẫu nhiên: là biến cố không thể biết trước được có xảy ra hay không.
Lời giải
a) Vì 1 con xúc xắc có số chấm là: 1; 2; 3; 4; 5; 6.
Tổng số chấm xuất hiện trên hai con xúc xắc có giá trị nhỏ nhất là: 1 + 1 = 2 > 1.
Biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc là một số lớn hơn 1” là biến cố chắc chắn.
b) Biến cố này là biến cố ngẫu nhiên vì ta không thể biết trước nó có xảy ra hay không. Chẳng hạn, nếu ta gieo được hai con xúc xắc là 3 và 4 thì biến cố xảy ra; còn nếu gieo hai con xúc xắc là 2 và 4 thì biến cố không xảy ra .
Bài 8. Chọn ngẫu nhiên một số trong bốn số 11;12;13 và 14. Tìm xác suất để:
a) Chọn được số chia hết cho 5.
b) Chọn được số có hai chữ số.
c) Chọn được số nguyên tố.
d) Chọn được số chia hết cho 6.
Phương pháp
Kiểm tra khả năng xảy ra của biến cố.
Lời giải
a) Không có số nào chia hết cho 5 nên xác suất để chọn được số chia hết cho 5 là 0.
b) Cả 4 số đều là số có hai chữ số nên xác suất để chọn được số có hai chữ số là 1.
c) Có hai số (11; 13) là số nguyên tố nên xác suất để chọn được số nguyên tố là \(\frac{2}{4} = \frac{1}{2}\).
d) Có một số (12) chia hết cho 6 nên xác suất để chọn được số chia hết cho 6 là \(\frac{1}{4}\).
Bài 9. Một hộp có \(12\) chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \(1,\,2,\,3,.....,\,12;\) hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Xét biến cố “Số xuất hiện trên thẻ được rút ra 1 số là hợp số”. Tìm xác suất của biến cố trên.
Phương pháp
Tính số kết quả thuận lợi cho biến cố A, B, C.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể.
Lời giải
Có 6 kết quả có thể xảy ra khi lấy ngẫu nhiên 1 thẻ từ hộp, đó là: 2; 3; 5; 8; 13; 21.
+) Có 4 số lẻ là 3; 5; 13; 21 nên số kết quả thuận lợi cho biến cố A là 4.
Xác suất của biến cố A: “Số ghi trên thẻ là số lẻ” là: \(\frac{4}{6} = \frac{2}{3}\).
+) Có 4 số nguyên tố là: 2; 3; 5; 13 nên số kết quả thuận lợi cho biến cố B là 4.
Xác suất của biến cố B: “Số ghi trên thẻ là số nguyên tố” là: \(\frac{4}{6} = \frac{2}{3}\).
+) Không có số chính phương trong các số trên nên số kết quả thuận lợi cho biến cố C là 0.
Xác suất của biến cố C: “Số ghi trên thẻ là số chính phương” là: \(\frac{0}{6} = 0\).
Bài 10. Cho \(\Delta MNP\) vuông tại M có MN < MP, kẻ đường phân giác NI của góc MNP (I thuộc MP). Kẻ IK vuông góc với NP tại K.
a) Chứng minh \(\Delta IMN = \Delta IKN\)
b) Chứng minh \({\rm{MI }} < {\rm{ IP}}\).
c) Gọi Q là giao điểm của đường thẳng IK và đường thẳng MN, đường thẳng NI cắt QP tại D. Chứng minh \(ND \bot QP\) và \(\Delta QIP\) cân tại I.
Phương pháp
a) Chứng minh \(\Delta IMN = \Delta IKN\)(cạnh huyền - góc nhọn)
b) Chứng minh \(IM = IK\), IP > IK nên IP > IM.
c) Chứng minh I là trực tâm của tam giác QNP nên \(ND \bot QP\).
Chứng minh \(\Delta NQP\) cân tại \(N\) nên DQ = DP.
\(\Delta QIP\) có \(ID\) vừa là đường cao, vừa là đường trung tuyến nên \(\Delta QIP\) cân tại \(I\)
Lời giải
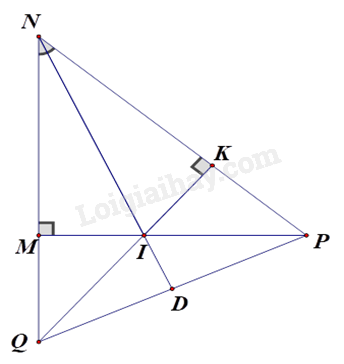
a) Xét \(\Delta IMN\) và \(\Delta IKN\) có:
\(\widehat {IMN} = \widehat {IKN} = {90^0}\)
NI chung
\(\widehat {MNI} = \widehat {KNI}\) (NI là đường phân giác NI của góc MNP)
suy ra \(\Delta IMN = \Delta IKN\)(cạnh huyền - góc nhọn) (đpcm)
b) Vì \(\Delta IMN = \Delta IKN\) nên IM = IK (hai cạnh tương ứng) (1)
Vì \(\Delta IKP\) vuông tại K nên IP > IK (2)
Từ (1) và (2) suy ra IP > IM (đpcm)
c) Xét \(\Delta NQP\) có đường cao QK và PM cắt nhau tại I nên I là trực tâm của tam giác NQP.
Do đó \(ND \bot QP\) (đpcm)
Vì \(\Delta NQP\) có ND vừa là đường cao vừa là đường phân giác nên \(\Delta NQP\) cân tại N.
Suy ra ND là đường trung tuyến của tam giác NQP hay QD = DP.
Xét \(\Delta QIP\) có ID vừa là đường cao vừa là đường trung tuyến nên \(\Delta QIP\) cân tại I.
Bài 11. Cho \(\Delta MNP\) cân tại M \(\left( {\widehat M < {{90}^0}} \right)\). Kẻ NH \( \bot \)MP \(\left( {H \in MP} \right)\), PK \( \bot \)MN \(\left( {K \in MN} \right)\). NH và PK cắt nhau tại E.
a) Chứng minh \(\Delta NHP = \Delta PKN\)
b) Chứng minh \(\Delta \)ENP cân.
c) Chứng minh ME là đường phân giác của góc NMP.
Phương pháp
a) Chứng minh \(\Delta NHP = \Delta PKN\) theo trường hợp cạnh huyền – góc nhọn.
b) Chứng minh \(\widehat {{P_1}} = \widehat {{N_1}}\) nên \(\Delta ENP\) cân.
c) Chứng minh MK = MH.
Chứng minh \(\Delta MEK = \Delta MEH\) (cạnh huyền – cạnh góc vuông) suy ra \(\widehat {{M_1}} = \widehat {{M_2}}\).
Do đó ME là đường phân giác của góc NMP.
Lời giải
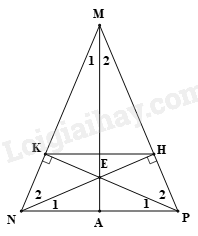
a) Xét \(\Delta NHP\) và \(\Delta PKN\) vuông tại H và K có:
\(\widehat {NPH} = \widehat {PNK}\) (vì \(\Delta MNP\) cân tại M)
\(NP\) chung
Suy ra \(\Delta NHP = \Delta PKN\) (cạnh huyền – góc nhọn) (đpcm)
b) Vì \(\Delta NHP = \Delta PKN\)nên \(\widehat {{N_1}} = \widehat {{P_1}}\).
Do đó \(\Delta ENP\) cân tại E (đpcm)
c) Ta có:
\(MK = MN - NK\) (vì K thuộc MN)
\(MH = MP - HP\) (vì H thuộc MP)
Mà \(MN = MP\) (vì \(\Delta MNP\) cân tại M)
\(NK = PH\) (vì \(\Delta NHP = \Delta PKN\))
suy ra \(MK = MH\).
Xét \(\Delta MEK\) và \(\Delta MEH\) vuông tại K và H có:
ME là cạnh chung
MK = MH (cmt)
Suy ra \(\Delta MEK = \Delta MEH\) (ch – cgv)
Suy ra \(\widehat {{M_1}} = \widehat {{M_2}}\) suy ra ME là tia phân giác của góc NMP (đpcm)
Bài 12. Cho \(\Delta ABC\) cân tại \(A\), có đường trung tuyến \(AM.\)
a) Chứng minh \(\Delta ABM = \Delta ACM.\)
b) Từ điểm \(M\) vẽ đường thẳng \(ME\) vuông góc với \(AB{\rm{ }}\left( {E \in AB} \right)\) và vẽ đường thẳng \(MF\) vuông góc với \(AC{\rm{ }}\left( {F \in AC} \right)\). Chứng minh \(ME = MF\).
Phương pháp
a) Chứng minh \(\Delta ABM = \Delta ACM\) theo trường hợp cạnh – góc – cạnh.
b) Chứng minh \(\Delta BEM = \Delta CFM\) suy ra ME = MF.
Lời giải
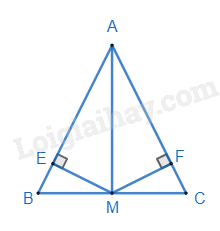
a) Vì tam giác ABC cân tại A nên ta có \(AB = AC,\widehat B = \widehat C\).
Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC, ta có: BM = MC.
Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB = AC\) (cmt)
\(\widehat B = \widehat C\) (cmt)
\(BM = CM\) (cmt)
Suy ra \(\Delta ABM = \Delta ACM\) (c.g.c) (đpcm)
b) Xét \(\Delta BEM\) và \(\Delta CFM\) có:
\(\widehat E = \widehat F = {90^o}\) (gt)
\(\widehat B = \widehat C\) (cmt)
\(BM = CM\) (cmt)
Suy ra \(\Delta BEM = \Delta CFM\) (ch.gn)
Suy ra ME = MF (hai cạnh tương ứng).
Bài 13*. Tính giá trị của biểu thức: \(N = x{y^2}{z^3} + {x^2}{y^3}{z^4} + {x^3}{y^4}{z^5} + ... + {x^{2022}}{y^{2023}}{z^{2024}}\), tại x = -1, y = -1, z = -1
Phương pháp
Biến đổi N thành \(N = xyz.y{z^2} + {x^2}{y^2}{z^2}.y{z^2} + {x^3}{y^3}{z^3}.y{z^2} + ... + {x^{2022}}{y^{2022}}{z^{2022}}.y{z^2}\)
Thay giá trị của \(y{z^2}\) theo y = -1, z = -1 vào N để rút gọn N.
Thay giá trị của \(xyz\) theo x = -1, y = -1, z = -1 để tính giá trị của N.
Lời giải
Ta có \(N = xyz.y{z^2} + {x^2}{y^2}{z^2}.y{z^2} + {x^3}{y^3}{z^3}.y{z^2} + ... + {x^{2022}}{y^{2022}}{z^{2022}}.y{z^2}\)
Tại y = -1, z = -1 ta được \(y{z^2} = - 1.{\left( { - 1} \right)^2} = - 1\).
Thay vào N, ta được:
\(N = - xyz - {x^2}{y^2}{z^2} - {x^3}{y^3}{z^3} - ... - {x^{2022}}{y^{2022}}{z^{2022}}\)
\( = - \left( {xyz} \right) - {\left( {xyz} \right)^2} - {\left( {xyz} \right)^3} - ... - {\left( {xyz} \right)^{2022}}\)
Tại x = -1, y = -1, z = -1 ta được \(xyz = \left( { - 1} \right).\left( { - 1} \right).\left( { - 1} \right) = - 1\).
Thay vào N, ta được:
\(N = - \left( { - 1} \right) - {\left( { - 1} \right)^2} - {\left( { - 1} \right)^3} - ... - {\left( { - 1} \right)^{2022}}\)
\(N = 1 - 1 + 1 - 1 + ... + 1 - 1 = 0\)
Vậy N = 0
Bài 14*. Cho biểu thức \(A = \frac{3}{4} + \frac{8}{9} + \frac{{15}}{{16}} + ... + \frac{{9999}}{{10000}}\) . Chứng minh rằng A < 99
Phương pháp
Biến đổi các phân số trong A thành hiệu của 1 trừ đi phân số có tử số là 1. (ví dụ: \(\frac{3}{4} = 1 - \frac{1}{4}\)).
Nhóm các số 1 thành 1 nhóm, các phân số còn lại thành một nhóm, ta được
\(A = 99 - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{100}^2}}}} \right)\).
Chứng minh \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{100}^2}}} > 0\) nên \(A = 99 - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{100}^2}}}} \right) < 0\)hay A < 99.
Lời giải
Ta có:
\(A = \frac{3}{4} + \frac{8}{9} + \frac{{15}}{{16}} + ... + \frac{{9999}}{{10000}}\)
\( = \left( {1 - \frac{1}{4}} \right) + \left( {1 - \frac{1}{9}} \right) + \left( {1 - \frac{1}{{16}}} \right) + ... + \left( {1 - \frac{1}{{10000}}} \right)\)
\( = \left( {1 - \frac{1}{{{2^2}}}} \right) + \left( {1 - \frac{1}{{{3^2}}}} \right) + \left( {1 - \frac{1}{{{4^2}}}} \right) + ... + \left( {1 - \frac{1}{{{{100}^2}}}} \right)\)
= \(99 - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{100}^2}}}} \right) = 99 - B\)
với B = \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{100}^2}}}\) > 0 nên A < 99.
Bài 15*. Cho ba số \(x,y,z\) khác \(0\) thỏa mãn \(\frac{{y + z - x}}{x} = \frac{{z + x - y}}{y} = \frac{{x + y - z}}{z}\).
Tính giá trị biểu thức \(P = \left( {1 + \frac{x}{y}} \right)\left( {1 + \frac{y}{z}} \right)\left( {1 + \frac{z}{x}} \right)\).
Phương pháp
Quy đồng mẫu biểu thức P ta được \(P = \frac{{x + y}}{y} \cdot \frac{{y + z}}{z} \cdot \frac{{z + x}}{x}\)
Ta có hai trường hợp:
TH1: \(x + y + z = 0\)
Ta có \(x + y = - z;y + z = - x;z + x = - y\), thay vào P để tính giá trị của P.
TH2: \(x + y + z \ne 0\)
Áp dụng tính chất dãy tỉ số bằng nhau với \(\frac{{y + z - x}}{x} = \frac{{z + x - y}}{y} = \frac{{x + y - z}}{z}\), ta suy ra \(y + z = 2x;z + x = 2y;x + y = 2z\). Thay vào P, ta tính được giá trị của P.
Lời giải
Ta có: \(P = \left( {1 + \frac{x}{y}} \right)\left( {1 + \frac{y}{z}} \right)\left( {1 + \frac{z}{x}} \right) = \frac{{x + y}}{y} \cdot \frac{{y + z}}{z} \cdot \frac{{z + x}}{x}\).
TH1: Nếu \(x + y + z = 0\) thì \(x + y = - z;y + z = - x;z + x = - y\).
Thay vào P ta được: \(P = \frac{{ - z}}{y} \cdot \frac{{ - x}}{z} \cdot \frac{{ - y}}{x} = - 1\).
TH2: Nếu \(x + y + z \ne 0\)
Theo bài ra ta có: \(\frac{{y + z - x}}{x} = \frac{{z + x - y}}{y} = \frac{{x + y - z}}{z}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được
\(\frac{{y + z - x}}{x} = \frac{{z + x - y}}{y} = \frac{{x + y - z}}{z}\)
\( = \frac{{y + z - x + z + x - y + x + y - z}}{{x + y + z}}\)
\( = \frac{{x + y + z}}{{x + y + z}} = 1\)
Suy ra \(\frac{{y + z - x}}{x} = \frac{{z + x - y}}{y} = \frac{{x + y - z}}{z} = 1\) hay \(y + z - x = x;z + x - y = y;x + y - z = z\)
\( \Rightarrow y + z = 2x;z + x = 2y;x + y = 2z\).
Thay vào P, ta được \(P = \frac{{2z}}{y} \cdot \frac{{2x}}{z} \cdot \frac{{2y}}{x} = 8\).
Vậy \(P = - 1\) hoặc \(P = 8\).
-
Đề thi học kì 2 Toán 7 - Đề số 1 - Chân trời sáng tạo
I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
-
Đề thi học kì 2 Toán 7 - Đề số 2 - Chân trời sáng tạo
I. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
-
Đề thi học kì 2 Toán 7 - Đề số 3 - Chân trời sáng tạo
I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
-
Đề thi học kì 2 Toán 7 - Đề số 4 - Chân trời sáng tạo
I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
-
Đề thi học kì 2 Toán 7 - Đề số 5 - Chân trời sáng tạo
I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.