Đề thi học kì 1 Toán 7 - Đề số 2 - Chân trời sáng tạoTải vềI. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
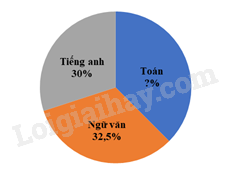
Đề bài Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Trong các phân số: −1018;1018;15−27;−2036;−2527;−−40−72, những phân số nào biểu diễn số hữu tỉ −59? A. 1018;15−27;−2036;−−40−72 B. −1018;1018;15−27;−−40−72 C. −1018;15−27;−2036;−−40−72 D. −1018;15−27;−2527;−−40−72 Câu 2: Tìm x biết: x2+19=53:3 A. x∈{49;−49} B. x∈{23;−23} C. x=49 D. x=23 Câu 3: Để lát một mảnh sân hình vuông có diện tích 100m2, người ta cần dùng bao nhiêu viên gạch hình vuông có cạnh dài 50cm (coi các mạch ghép là không đáng kể)? A. 350 viên gạch B. 420 viên gạch C. 380 viên gạch D. 400 viên gạch Câu 4: Với mọi số thực x. Khẳng định nào sau đây là sai? A. |x|≥x B. |x|≥−x C. |x|2=x2 D. ||x||=x Câu 5: Ông Minh làm một khối gỗ hình lăng trụ đứng tam giác có kích thước như hình vẽ bên dưới để chèn bánh xe. Tính thể tích của khối gỗ. A. 0,189m3 B. 189000m3 C. 189m3 D. 18,9m3 Câu 6: Một khối gỗ dạng hình hộp chữ nhật có kích thước như hình bên dưới. Tính diện tích xung quanh của khối gỗ. A. 640cm2 B. 2400cm2 C. 6400cm2 D. 240cm2 Câu 7: Cho góc ∠xOy=70∘ và góc ∠uOv là góc đối đỉnh của góc ∠xOy. Tính số đo góc ∠uOv? A. 80∘ B. 140∘ C. 130∘ D.70∘ Câu 8: Phát biểu nào sau đây là sai? A. Hai đường thẳng không có điểm chung thì song song. B. Qua điểm M nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng ấy. C. Hai đường thẳng không cắt nhau là hai đường thẳng phân biệt. D. Nếu một đường thẳng cắt hai đường thẳng tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song. Câu 9: Số học sinh đăng ký học bổ trợ các Câu lạc bộ Toán, Ngữ văn, Tiếng anh của lớp 7 của một trường được biểu diễn qua biểu đồ hình quạt tròn như sau:
Tính số phần trăm học sinh đăng ký môn Toán là bao nhiêu? A. 40% B. 37,5% C. 30% D. 35% Câu 10: Đâu không là một yếu tố của một biểu đồ đoạn thẳng? A. Trục ngang B. Các đoạn thẳng C. Đường chéo D. Tên biểu đồ Phần II. Tự luận (7 điểm): Bài 1: (2,0 điểm) Thực hiện phép tính: a) 52+12:(−34).49−42−(−2)3 b) (32)2−[0,5:2−√81.(−12)2] c) (−√0,04).√0,01+12,02 d) |√169−√900|−|−54|:(13−12)2 Bài 2: (2,0 điểm) Tìm x, biết: a) 0,2x+(25x−1,7x)=−1110 b) (x+0,8)2=14 c) 5x+4−3.5x+3=2.511 d) 30−|2x+1|=13 Bài 3: (1,0 điểm) a) Sắp xếp các số sau theo thứ tự tăng dần: 6;√46;0;−√81;−3,6;2.√16 b) Sắp xếp các số sau theo thứ tự giảm dần: √78;√50+4;−8;−3.√0,25;0;6 Bài 4: (1,0 điểm) Chi đội của bạn Hòa dựng một lều ở trại hè có dạng hình lăng trụ đứng tam giác với kích thước như hình vẽ bên dưới.
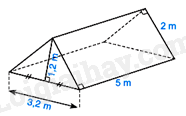
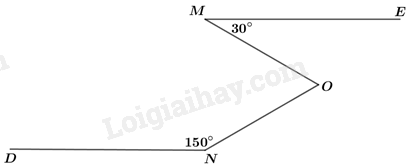
a) Tính thể tích khoảng không bên trong lều. b) Biết lều phủ bạt 4 phía, trừ mặt tiếp đất. Tính diện tích vải bạt cần phải có để dựng lều. Bài 5: (1,0 điểm) Cho hình vẽ dưới, biết số đo các góc ^EMO=30∘, ^DNO=150∘, ^MON=60∘. Chứng minh ME//DN.
-----HẾT----- Lời giải Phần I: Trắc nghiệm:
Câu 1 Phương pháp: Thực hiện rút gọn, tìm các phân số bằng phân số −59. Cách giải: Ta có: Ta có: −1018=−59;1018=59≠−59;15−27=5−9=−59;−2036=−59=−59;−2527≠−59;−−40−72=−4072=−59=−59. Vậy những phân số biểu diễn số hữu tỉ −59 là: −1018;15−27;−2036;−−40−72. Chọn C. Câu 2 Phương pháp: Thực hiện phép chia hai số hữu tỉ Vận dụng quy tắc chuyển vế Cách giải: x2+19=53:3 x2+19=53.13=59x2=59−19x2=49x2=(23)2=(−23)2 ⇒x=23 hoặc x=−23 Vậy x∈{23;−23} Chọn B. Câu 3 Phương pháp: Tính diện tích của một viên gạch: hình vuông có độ dài một cạnh bằng a(a>0) thì diện tích của hình vuông được tính theo công thức: S=a2 Số viên gạch cần dùng = diện tích của mảnh sân : diện tích của một viên gạch. Cách giải: Diện tích của một viên gạch hình vuông là: 50.50=2500(cm2)=0,25(m2) Số viên gạch cần dùng đến là: 100:0,25=100:25100=100.10025=400 (viên gạch) Vậy người ta cần dùng 400 viên gạch để lát sân. Chọn A. Câu 4 Phương pháp: Vận dụng kiến thức về dấu giá trị tuyệt đối: |x|={xkhix≥0−xkhix<0 Cách giải: Ta có: |x|={xkhix≥0−xkhix<0 nên đáp án A, B và C đúng. Đáp án D sai với mọi x<0 Chọn D. Câu 5 Phương pháp: Thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác: V=Sđáy.h Trong đó: V: thể tích của hình lăng trụ đứng Sđáy: diện tích một đáy của hình lăng trụ đứng h: chiều cao của hình lăng trụ đứng Diện tích tam giác có đáy là a, chiều cao tương ứng là h được tính theo công thức: S=12a.h Cách giải: Diện tích đáy của hình lăng trụ là: S=12.90.60=2700(cm2) Thể tích của khối gỗ là: V=Sđáy.h=70.2700=189000(cm3)=0,189(m3) Chọn A. Câu 6 Phương pháp: Diện tích xung quanh của hình hộp chữ nhật có chiều dài đáy là a, chiều rộng đáy là b và chiều cao là c: Sxq=2.(a+b).c Cách giải: Diện tích xung quanh của khối gỗ là: Sxq=2.(20+12).10=640(cm2) Chọn A. Câu 7 Phương pháp: Hai góc đổi đỉnh thì bằng nhau. Cách giải: Vì ∠xOy và ∠uOv là hai góc đối đỉnh nên ∠xOy=∠uOv=70∘ Chọn D. Câu 8 Phương pháp: Áp dụng tiên đề Euclid về đường thẳng song song, dấu hiệu nhận biết hai đường thẳng song song. Cách giải: A. Đúng, theo định nghĩa hai đường thẳng song song. B. Đúng, theo tiên đề Euclid. C. Sai, vì nó có thể là hai đường thẳng trùng nhau. D. Đúng, theo dấu hiệu nhận biết hai đường thẳng song song. Chọn C. Câu 9 Phương pháp: Đọc và phân tích dữ liệu của biểu đồ hình quạt tròn. Cách giải: Số phần trăm học sinh đăng ký môn Toán là: 100%−32,5%−30%=37,5% Chọn B. Câu 10 Phương pháp: Nhận ra các thành phần của biểu đồ đoạn thẳng. Cách giải: Trục ngang, các đoạn thẳng, tên biểu đồ đều là các yếu tố của một biểu đồ đoạn thẳng. Trong biểu đồ đoạn thẳng, không có yếu tố đường chéo. Chọn C.
Phần II. Tự luận (7 điểm): Bài 1 Phương pháp: a) Thực hiện phép cộng, trừ, nhân, chia với số hữu tỉ Vận dụng kiến thức lũy thừa của một số. b) Thực hiện phép cộng, trừ, nhân, chia với số hữu tỉ Lũy thừa của một số hữu tỉ: (ab)n=anbn(b≠0;n∈Z) Thực hiện phép tính với căn bậc hai của một số c) Thực hiện phép cộng, trừ, nhân, chia với số hữu tỉ Thực hiện phép tính với căn bậc hai của một số d) Thực hiện phép cộng, trừ, nhân, chia với số hữu tỉ Thực hiện phép tính với căn bậc hai của một số Vận dụng kiến thức giá trị tuyệt đối của một số thực: |x|={xkhix>0−xkhix<00khix=0 Cách giải: a) 52+12:(−34).49−42−(−2)3 =52+12.−43.49−16−(−8)=52+−827−16+8=52+−827−8=13554+−1654−43254=−31354 b) (32)2−[0,5:2−√81.(−12)2] =3222−[12:2−9.(−1)222]=94−(12.12−9.14)=94−(14−94)=94−(−84)=174 c) (−√0,04).√0,01+12,02 =(−0,2).0,1+12,02=−0,02+12,02=12 d) |√169−√900|−|−54|:(13−12)2 =|13−30|−54:(26−36)2=|−17|−54:(−16)2=17−54:136=17−54.36=17−45=−28 Bài 2 Phương pháp: a) Vận dụng quy tắc chuyển vế, tìm x b) Biến đổi để có cùng lũy thừa từ đó tìm được x c) Biến đổi để có cùng cơ số từ đó tìm được x. d) |x|=a Trường hợp a<0, khi đó phương trình không có nghiệm x Trường hợp a>0, vận dụng kiến thức giá trị tuyệt đối của một số thực: |x|={xkhix>0−xkhix<00khix=0 Cách giải: a) 0,2x+(25x−1,7x)=−1110 0,2x+0,4x−1,7x=−1,1(0,2+0,4−1,7).x=−1,1−1,1x=−1,1x=−1,1:(−1,1)x=1 Vậy x=1 b) (x+0,8)2=14 (x+0,8)2=0,25(x+0,8)2=0,52=(−0,5)2 Trường hợp 1: x+0,8=0,5x=0,5−0,8x=−0,3 Trường hợp 2: x+0,8=−0,5x=−0,5−0,8x=−1,3 Vậy x∈{−0,3;−1,3} c) 5x+4−3.5x+3=2.511 5x+3+1−3.5x+3=2.5115x+3.5−3.5x+3=2.511(5−3).5x+3=2.5112.5x+3=2.5115x+3=511x+3=11x=11−3x=8 Vậy x=8 d) 30−|2x+1|=13 1−|2x−1|=−13|2x−1|=1−13|2x−1|=33−13|2x−1|=23 Trường hợp 1: 2x−1=232x=23+1=23+332x=53x=53:2=53.12x=56 Vậy x∈{56;16} Trường hợp 2: 2x−1=−23 2x=−23+1=−23+332x=13x=13:2=13.12x=16 Bài 3 Phương pháp: Tính căn bậc hai số học của các căn bậc hai, sau đó so sánh. Cách giải: a) 6;√46;0;−√81;−3,6;2.√16 + Vì 36<46<49 nên √36<√46<√49 hay 6<√46<7 2.√16=2.√42=2.4=8>7 Suy ra 0<6<√46<2.√16 (1) + Ta có: −√81=−√92=−9 Vì 3,6<9 nên −3,6>−9 suy ra −3,6>−√81 Suy ra 0>−3,6>−√81 (2) Từ (1) và (2), suy ra −√81<−3,6<0<6<√46<2.√16 Vậy thứ tự tăng dần của các số là: −√81;−3,6;0;6;√46;2.√16. b) √78;√50+4;−8;−3.√0,25;0;6 + Vì 64<78 nên √64<√78 hay 8<√78 Ta có: √50+4=√54 Vì 49<54<64 nên √49<√54<√64 hay 7<√54<8 Vì 0<6<7<√54<8<√78 nên 0<6<√54<√78 (1) Suy ra 0<6<√50+4<√78 + Ta có: −3.√0,25=−3.√0,52=−3.0,5=−3.12=−32=−1,5 Vì 1,5<8 nên −1,5>−8 Suy ra 0>−3.√0,25−8 (2) Từ (1) và (2), suy ra −8<−3.√0,25<0<6<√50+4<√78 Vậy thứ tự giảm dần của các số là: √78;√50+4;6;0;−3√0,25;−8. Bài 4 Phương pháp: a) Thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác: V=Sđáy.h Trong đó: V: thể tích của hình lăng trụ đứng Sđáy: diện tích một đáy của hình lăng trụ đứng h: chiều cao của hình lăng trụ đứng Diện tích tam giác có đáy là a, chiều cao tương ứng là h được tính theo công thức: S=12a.h b) Diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác: Sxq=C.h Trong đó: Sxq: diện tích xung quanh của hình lăng trụ C: chu vi một đáy của hình lăng trụ h: chiều cao của lăng trụ Cách giải: a) Diện tích đáy lăng trụ là: Sđáy =12.3,2.1,2=1,92(m2) Thể tích khoảng không bên trong lều là: V=Sđáy.h=1,92.5=9,6(m3) b) Diện tích vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là 5m và 3,2m. Diện tích xung quanh lăng trụ là: Sxq=C.h=(2+2+3,2).5=36(m2) Diện tích toàn phần của hình lăng trụ là: Stp=2xq+2Sđáy=36+2.1,92=39,84(m2) Diện tích mặt bên kích thước 5m và 3,2m là: 5.3,2=16(m2) Diện tích vải bạt cần có để dựng lều là: 39,84−16=23,84(m2) Bài 5 Phương pháp: Áp dụng tính chất hai đường thẳng song song. Áp dụng dấu hiệu nhận biết hai đường thẳng song song. Cách giải:
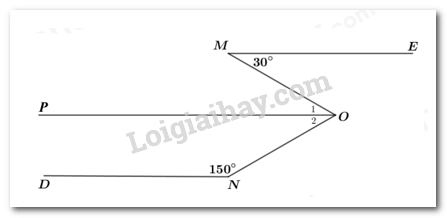
Kẻ OP//ME (1) Vì OP//ME nên ∠M=∠O1=30∘ (2 góc so le trong) Ta có ∠MON=∠O1+∠O2⇒∠O2=∠MON−∠O1=60∘−30∘=30∘ Lại có: ∠O2+∠N=30∘+150∘=180∘ Mà 2 góc ở vị trí trong cùng phía nên OP//DN (2) Từ (1) và (2) suy ra ME//DN
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|