Đề thi giữa kì 2 Toán 7 - Đề số 2 - Chân trời sáng tạo

Đề bài

I. TRẮC NGHIỆM ( 3 điểm)

Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1. Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên ta được

A. 12,5 : 34,5;

B. 29 : 65;

C. 25 : 69;

D. 1 : 3.

Câu 2. Biết 7x = 4y và y – x = 24. Khi đó, giá trị của x, y là

A. x = −56, y = −32;

B. x = 32, y = 56;

C. x = 56, y = 32;

D. x = 56, y = −32.

Câu 3. Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?

A. –6;

B. 0;

C. –9;

D. –1.

Câu 4. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng:

A. –32;

B. 32;

C. –2;

D. 2.

Câu 5. Biểu thức đại số biểu thị “Lập phương của tổng của hai số x và y” là

A. x³ – y³;

B. x + y;

C. x³ + y³;

D. (x + y)³.

Câu 6. Một tam giác có ba góc có số đo tỉ lệ với 3,4,5. Số đo ba góc của tam giác lần lượt là:

A. 45⁰; 60⁰; 75⁰;

B. 30⁰; 60⁰; 90⁰;

C. 20⁰; 60⁰; 100⁰;

D. Một kết quả khác.

Câu 7. Cho tam giác $MNP$ có $MN = MP$. Gọi $A$ là trung điểm của $NP$. Nếu $\angle NMP = {50^0}$ thì số đo của $\angle MPN$ là:

A. ${100^0}$.

B. ${130^0}$.

C. ${50^0}$.

D. ${65^0}$.

Câu 8. Cho tam giác $ABC$ vuông tại $A$ $\left( {AB > AC} \right)$. Tia phân giác của góc $B$ cắt $AC$ ở $D$. Kẻ $DH$ vuông góc với $BC$.Chọn câu đúng.

A. $BH = BD$.

B. $BH > BA$.

C. $BH < BA$.

D. $BH = BA$.

Câu 9. Cho tam giác MNP có: $\widehat N = 70^\circ ;\widehat P = 55^\circ$. Khẳng định nào sau đây là đúng ?

A. MP < MN;

B. MP = MN;

C. MP > MN;

D. Không đủ dữ kiện so sánh.

Câu 10. Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng?

A. DN = DP;

B. MD < MP;

C. MD > MN;

D. MN = MP.

Câu 11. Bộ ba độ dài đoạn thẳng nào sau đây không thể tạo thành một tam giác?

A. 18cm; 28cm; 10cm;

B. 5cm; 4cm; 6cm;

C. 15cm; 18cm; 20cm;

D. 11cm; 9cm; 7cm.

Câu 12. Cho G là trọng tâm tam giác MNP có trung tuyến MK. Khẳng định nào sau đây là đúng?

A. $\dfrac{{MG}}{{GK}} = \dfrac{1}{2}$;

B. $\dfrac{{MG}}{{MK}} = \dfrac{1}{3}$ ;

C. $\dfrac{{KG}}{{MK}} = \dfrac{1}{3}$;

D. $\dfrac{{MG}}{{MK}} = \dfrac{2}{3}$.

II. PHẦN TỰ LUẬN (7,0 điểm)

Bài 1. (2 điểm) Tìm $x$ biết:

a) $x - \dfrac{2}{5} = \dfrac{{ - 9}}{{10}}$

b) $\dfrac{3}{4} + \dfrac{1}{4}x = \dfrac{{ - 5}}{6}$

c) $\dfrac{{x - 1}}{3} = \dfrac{{2 - x}}{{ - 2}}$

Bài 2. (2 điểm) Tính chu vi của hình chữ nhật biết rằng chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với $5\,\,;\,\,3$ và hai lần chiều dài hơn ba lần chiều rộng là 8 cm.

Bài 3. (2,5 điểm) Cho $\Delta ABC$ vuông tại $A$, đường trung tuyến $AM$. Trên tia đối của tia $MA$ lấy điểm $D$ sao cho $DM = MA$.

a) Chứng minh $\Delta AMB = \Delta DMC$.

b) Trên tia đối của tia $CD$, lấy điểm $I$ sao cho $CI = CA$, qua điểm $I$ vẽ đường thẳng song song với $AC$ cắt $AB$ tại $E$. Chứng minh $\Delta ACE = \Delta ICE$, từ đó suy ra $\Delta ACE$ là tam giác vuông cân.

Bài 4. (0,5 điểm) Cho x,y,z thỏa mãn:$\dfrac{x}{2} = \dfrac{y}{5} = \dfrac{z}{7}$ với x,y,z khác 0. Tính:

$P = \dfrac{{x - y + z}}{{x + 2y - z}}$.

Lời giải

I. Trắc nghiệm

Câu 1.

Phương pháp

Nhân cả tử và mẫu của phân số với 1 số khác 0, ta được phân số có giá trị không đổi.

Lời giải

1,25 : 3,45 = 125 : 345 = 25 : 69.

Chọn C.

Câu 2.

Phương pháp

Áp dụng tính chất dãy tỉ số bằng nhau

Lời giải

Vì 7x = 4y nên $\dfrac{x}{4} = \dfrac{y}{7}$

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\dfrac{x}{4} = \dfrac{y}{7} = \dfrac{{y - x}}{{7 - 4}} = \dfrac{{24}}{3} = 8$

Do đó x = 4 . 8 = 32; y = 7 . 8 = 56.

Chọn B.

Câu 3.

Phương pháp

Đại lượng $y$ tỉ lệ thuận với $x$ theo hệ số tỉ lệ $k$ thì $y = kx$

Lời giải

Khi x = - 3 thì $y = kx = 2.( - 3) =  - 6$

Chọn A.

Câu 4.

Phương pháp

Tính chất hai đại lượng tỉ lệ nghịch: tích 2 giá trị tương ứng của 2 đại lượng luôn không đổi (bằng hệ số tỉ lệ)

Cách giải:

Hệ số tỉ lệ là: -12 . 8 = -96.

Khi x = 3 thì y = -96 : 3 = -32.

Chọn A

Câu 5.

Phương pháp

Mô tả

Cách giải:

Biểu thức đại số biểu thị “Lập phương của tổng của hai số x và y” là (x + y)³

Chọn D

Câu 6.

Phương pháp

Áp dụng:

Định lí Tổng định lí 3 góc trong một tam giác bằng 180 độ.

Tính chất của dãy tỉ số bằng nhau

Cách giải:

Gọi số đo 3 góc của tam giác lần lượt là a,b,c.

Vì tổng 3 góc trong một tam giác là 180 độ nên $a + b + c = 180^\circ$.

Do số đo ba góc tỉ lệ với 3;4;5 nên $\dfrac{a}{3} = \dfrac{b}{4} = \dfrac{c}{5}$.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\begin{array}{l}\dfrac{a}{3} = \dfrac{b}{4} = \dfrac{c}{5} = \dfrac{{a + b + c}}{{3 + 4 + 5}} = \dfrac{{180}}{{12}} = 15\\ \Rightarrow a = 15.3 = 45;\\b = 15.4 = 60;\\c = 15.5 = 75.\end{array}$

Chọn A.

Câu 7.

Phương pháp:

Vận dụng định lí:

+ Nếu ba cạnh của tam giác bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

+ Tổng ba góc trong một tam giác bằng ${180^0}$.

Cách giải:

* Vì $A$ là trung điểm của $NP$ nên $AN = AP$ (tính chất trung điểm của đoạn thẳng)

* Xét $\Delta AMN$ và $\Delta AMP$ có:

$MN = MP$ (giả thiết)

$AN = AP$ (chứng minh trên)

$AM$ là cạnh chung

Suy ra $\Delta AMN = \Delta AMP\,\left( {c.c.c} \right)$

Do đó, $\angle MNA = \angle MPA$ (hai góc tương ứng) hay $\angle MNP = \angle MPN$

Xét $\Delta MNP$ có: $\angle MNP + NPM + \angle NMP = {180^0}$ (tổng ba góc trong một tam giác)

$\begin{array}{l} \Rightarrow \angle MPN + \angle MPN + {50^0} = {180^0}\\ \Rightarrow 2\angle MPN = {180^0} - {50^0}\\ \Rightarrow 2\angle MPN = {130^0}\\ \Rightarrow \angle MPN = {130^0}:2\\ \Rightarrow \angle MPN = {65^0}\end{array}$

Vậy $\angle MPN = {65^0}$

Chọn D.

Câu 8.

Phương pháp:

Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh huyền – góc nhọn, từ đó suy ra cặp cạnh tương ứng bằng nhau.

Cách giải:

Xét $\Delta BAD$ và $\Delta BHD$ có:

                 $\angle BAD = \angle BHD = 90^\circ$

                  $BD$ chung

                 $\angle ABD = \angle HBD$ (vì $BD$ là tia phân giác $\angle B$)

$\Rightarrow \Delta ABD = \Delta HBD$ (cạnh huyền – góc nhọn)

$\Rightarrow BA = BH$(hai cạnh tương ứng).

Chọn D.

Câu 9.

Phương pháp: Áp dụng định lí tổng ba góc trong tam giác, tính góc M.

Dựa vào quan hệ giữa cạnh và góc đối diện trong tam giác.

Cách giải:

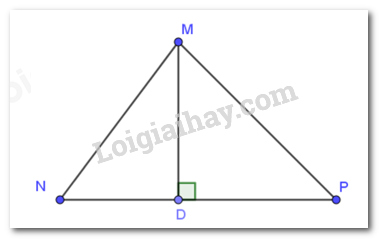
Xét tam giác MNP có: $\widehat M + \widehat N + \widehat P = 180^\circ$ (định lí tổng ba góc trong một tam giác)

$\Rightarrow \widehat M = 180^\circ  - \widehat N - \widehat P = 180^\circ  - 70^\circ  - 55^\circ  = 55^\circ$

Ta được: $\widehat M = \widehat P$

Mà cạnh NP là cạnh đối của góc M, MN là cạnh đối của góc P.

Vậy NP = MN.

Chọn B.

Câu 10:

Phương pháp: Sử dụng mối quan hệ đường xiên và hình chiếu.

Sử dụng quan hệ đường vuông góc và đường xiên.

Cách giải:

Trong tam giác MNP có MN < MP, hình chiếu của MN và MP trên cạnh NP lần lượt là ND và PD.

Do đó, ND < PD.

Ta có: MD < MP (đường vuông góc nhỏ hơn đường xiên)

Chọn B

Câu 11.

Phương pháp: Bất đẳng thức tam giác: Kiểm tra tổng độ dài 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất không. Nếu không thì bộ 3 độ dài đó không tạo được thành tam giác.

Cách giải:

Vì 18 + 10 = 28 nên không thỏa mãn bất đẳng thức tam giác.

Do đó, bộ ba độ dài đoạn thẳng 18 cm; 28 cm; 10 cm không thể tạo thành một tam giác.

Chọn A.

Câu 12.

Phương pháp

Nếu $\Delta ABC$ có trung tuyến $AM$ và trọng tâm $G$ thì $AG = \dfrac{2}{3}AM$

Lời giải

Vì G là trọng tâm tam giác MNP nên G là giao điểm của ba đường trung tuyến nên 

$MG = \dfrac{2}{3}MK;GK = \dfrac{1}{3}MK;MG = 2GK$

Chọn C.

II. PHẦN TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

a) + b) Thực hiện các phép toán với số hữu tỉ.

c) Vận dụng định nghĩa hai phân thức bằng nhau.

Cách giải:

a) $x - \dfrac{2}{5} = \dfrac{{ - 9}}{{10}}$

$\begin{array}{l}x = \dfrac{{ - 9}}{{10}} + \dfrac{2}{5}\\x = \dfrac{{ - 9 + 2.2}}{{10}}\\x = \dfrac{{ - 5}}{{10}} = \dfrac{{ - 1}}{2}\end{array}$

Vậy $x = - \dfrac{1}{2}$

b) $\dfrac{3}{4} + \dfrac{1}{4}x = \dfrac{{ - 5}}{6}$

$\begin{array}{l}\dfrac{1}{4}x = \dfrac{{ - 5}}{6} - \dfrac{3}{4}\\\dfrac{1}{4}x = \dfrac{{ - 5.2 - 3.3}}{{12}}\\\dfrac{1}{4}x = \dfrac{{ - 19}}{{12}}\\x = \dfrac{{ - 19}}{{12}}:\dfrac{1}{4}\\x = \dfrac{{ - 19}}{3}\end{array}$

Vậy $x = \dfrac{{ - 19}}{3}$

c) $\dfrac{{x - 1}}{3} = \dfrac{{2 - x}}{{ - 2}}$

$\begin{array}{l} - 2\left( {x - 1} \right) = 3\left( {2 - x} \right)\\ - 2x + 2 = 6 - 3x\\ - 2x + 3x = 6 - 2\\x = 4\end{array}$

Vậy $x = 4$

Câu 2 (1 điểm)

Phương pháp:

Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là $x,y$ (cm) (điều kiện: $x,y > 0$)

Áp dụng tính chất của dãy tỉ số bằng nhau.

Cách giải:

Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là $x,y$ (cm) (điều kiện: $x,y > 0$)

Theo đề bài: chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với $5\,\,;\,\,3$  nên ta có: $\dfrac{x}{5} = \dfrac{y}{3}$

Hai lần chiều dài hơn ba lần chiều rộng là $8$ cm nên $2x - 3y = 8$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: $\dfrac{x}{5} = \dfrac{y}{3} = \dfrac{{2x}}{{10}} = \dfrac{{3y}}{9} = \dfrac{{2x - 3y}}{{10 - 9}} = \dfrac{8}{1} = 8$

Khi đó, $\dfrac{x}{5} = 8 \Rightarrow x = 40$ (tmđk)

 $\dfrac{y}{3} = 8 \Rightarrow y = 24$ (tmđk)

Chu vi của hình chữ nhật là: $2\left( {x + y} \right) = 2\left( {40 + 24} \right) = 128$ (cm)

Bài 5. (2,0 điểm)

Phương pháp:

a) Ta sẽ chứng minh: $\Delta AMB = \Delta DMC\left( {c.g.c} \right)$

b) Ta sẽ chứng minh: $\angle EIC = {90^0}$, từ đó chứng minh được $\Delta ACE = \Delta ICE$(cạnh huyền – cạnh góc vuông)

$\Rightarrow \angle ACE = \angle ICE$ (hai góc tương ứng)

$\Rightarrow \Delta ACE$ vuông cân tại $A\left( {\angle EAC = {{90}^0}} \right)$

Cách giải:

a) $\Delta ABC$ vuông tại $A,AM$ là đường trung tuyến$\Rightarrow CM = BM$

Ta có: $\angle CMD = \angle AMB$ (hai góc đối đỉnh)

Xét $\Delta AMB$ và $\Delta DMC$ có:

$\left. \begin{array}{l}CM = BM\left( {cmt} \right)\\\angle CMD = \angle AMB\left( {cmt} \right)\\AM = MD\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta AMB = \Delta DMC\left( {c.g.c} \right)$

b) Ta có: $\Delta AMB = \Delta DMC\left( {cmt} \right) \Rightarrow \angle ABM = \angle DCM$ (hai góc tương ứng)

Mà hai góc $\angle ABM;\angle DCM$ ở vị trí so le trong

$\Rightarrow AB//CD$

Mà $AB \bot AC(\Delta ABC$ vuông tại $A)$

$\Rightarrow CD \bot AC$ tại $C \Rightarrow EI \bot CD$ tại $I$ (vì $EI//AC$) hay $\angle EIC = {90^0}$

Xét $\Delta ACE$ và $\Delta ICE$ có:

$\left. \begin{array}{l}\angle EAC = \angle EIC = {90^0}\\CE\,\,chung\\AC = IC\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta ACE = \Delta ICE$ (cạnh huyền – cạnh góc vuông)

$\Rightarrow \angle ACE = \angle ICE$ (hai góc tương ứng)

Mà $\angle ICE = \angle AEC$ (vì $AB//CD$)

$\Rightarrow \angle ACE = \angle AEC$

$\Rightarrow \Delta ACE$ vuông cân tại $A\left( {\angle EAC = {{90}^0}} \right)$

Bài 4. (0,5 điểm)

Phương pháp:

Đặt $\dfrac{x}{2} = \dfrac{y}{5} = \dfrac{z}{7} = k$

Cách giải:

Đặt $\dfrac{x}{2} = \dfrac{y}{5} = \dfrac{z}{7} = k \Rightarrow x = 2k;y = 5k;z = 7k.$

Ta có: $P = \dfrac{{x - y + z}}{{x + 2y - z}} = \dfrac{{2k - 5k + 7k}}{{2k + 2.5k - 7k}} = \dfrac{{4k}}{{5k}} = \dfrac{4}{5}.$         

Vậy $P = \dfrac{4}{5}.$