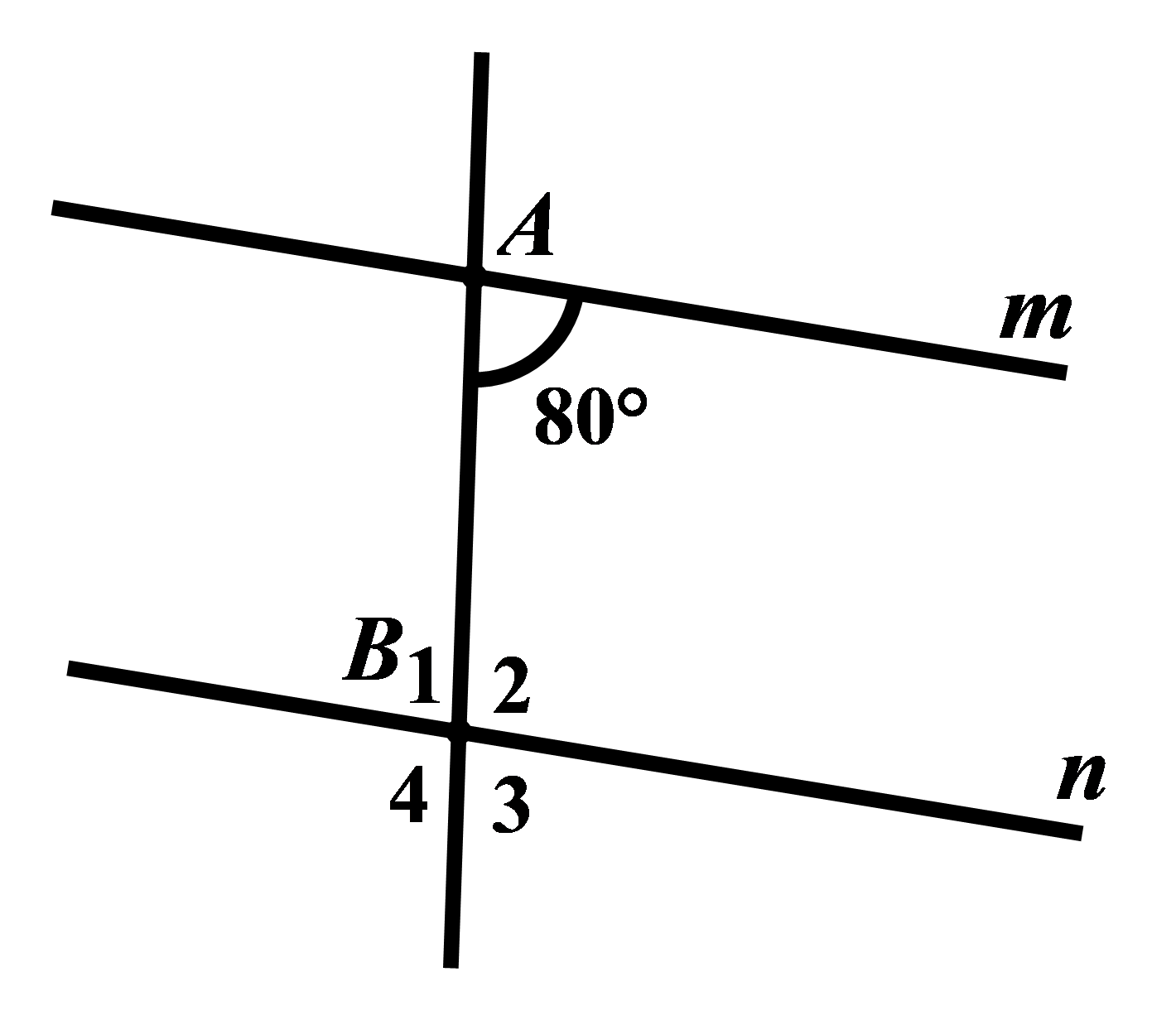Đề thi học kì 1 Toán 7 - Đề số 1 - Chân trời sáng tạoTải vềI. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
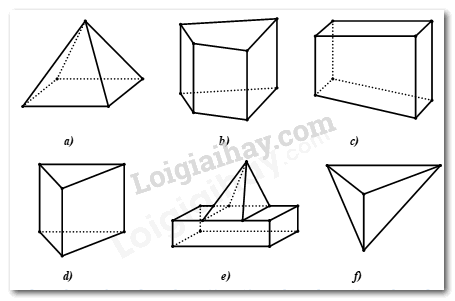
Đề bài Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Phát biểu nào sau đây là sai? A. Mọi số vô tỉ đều là số thực. B. Mọi số thực đều là số vô tỉ. C. Số 0 là số hữu tỉ. D. \( - \sqrt 2 \) là số vô tỉ. Câu 2: Một tam giác có độ dài cạnh \(\dfrac{2}{9}m\) và chiều cao ứng với cạnh đó bằng nửa cạnh đó. Tính diện tích của tam giác đã cho. A. \(\dfrac{1}{9}{m^2}\) B. \(\dfrac{1}{{18}}{m^2}\) C. \(\dfrac{2}{{81}}{m^2}\) D. \(\dfrac{1}{{81}}{m^2}\) Câu 3: Kết quả của phép tính: \(\left| {6 - \sqrt {34} } \right| + 3 + \sqrt {34} \) là: A. \(9 + 2\sqrt {34} \) B. \(3 + 2\sqrt {34} \) C. \(9\) D. \(3\) Câu 4: Cho biết \(1inch \approx 2,54cm\). Tính độ dài đường chéo bằng đơn vị một màn hình \(36inch\) và làm tròn đến hàng phần mười. A. \(91,54\,cm\) B. \(91,5\,cm\) C. \(91,44\,cm\) D. \(91,4\,cm\) Câu 5: Một hình lăng trụ đứng tứ giác có độ dài cạnh bên là \(20cm\) và đáy là hình thoi với độ dài hai đường chéo là \(18cm;30cm\). Tính thể tích của hình lăng trụ đó. A. \(6\,300\,c{m^3}\) B. \(5\,400\,c{m^3}\) C. \(3\,600c{m^3}\) D. \(4\,800\,c{m^3}\) Câu 6: Trong các hình vẽ dưới đây, liệt kê tất cả các hình là hình lăng trụ đứng tam giác hoặc hình lăng trụ đứng tứ giác? A. Tất cả 6 hình B. Hình a), c), e), f) C. Hình b), c), d) D. Hình b), d) Câu 7: Ở hình vẽ bên dưới có \(AB\) và \(CD\) cắt nhau tại \(O,Ot\) là tia phân giác của góc \(BOC\)\(,\angle AOC - \angle BOC = {68^0}\). Số đo góc \(BOt\) là:
A. \({56^0}\) B. \({62^0}\) C. \({28^0}\) D. \({23^0}\) Câu 8: Cho hình vẽ bên dưới, biết hai đường thẳng \(m\) và \(n\) song song với nhau. Tính số đo góc \({B_4}?\)
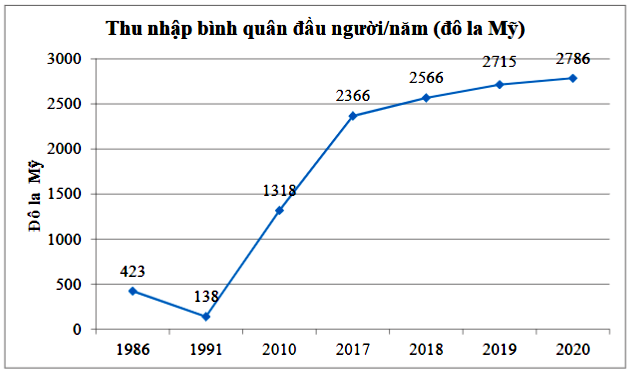
A. \({80^0}\) B. \({100^0}\) C. \({120^0}\) D. \({140^0}\) Câu 9: Biểu đồ hình quạt tròn dùng để: A. So sánh số liệu của hai đối tượng cùng loại. B. So sánh các thành phần trong toàn bộ dữ liệu. C. Biểu diễn sự thay đổi của một đại lượng theo thời gian. D. Biểu diễn sự chênh lệch số liệu giữa các đối tượng. Câu 10: Biểu đồ bên dưới biểu diễn thu nhập bình quân đầu người/năm của Việt Nam (tính theo đô la Mỹ) ở một số năm trong những gia đoạn từ 1986 đến 2020. Hãy cho biết năm nào Việt Nam có thu nhập cao nhất, cụ thể là bao nhiêu đô la?
A. Năm 1991, Việt Nam có mức thu nhập thấp nhất là 138 đô la/năm. B. Năm 2019, Việt Nam có mức thu nhập cao nhất là 2738 đô la/năm. C. Năm 2018, Việt Nam có mức thu nhập cao nhất là 2566 đô la/năm. D. Năm 2020, Việt Nam có mức thu nhập cao nhất là 2786 đô la/năm. Phần II. Tự luận (7 điểm): Bài 1: (2,0 điểm) Tính hợp lí (nếu có thể): a) \(\dfrac{{ - 15}}{{14}}:\dfrac{{17}}{{23}} - \dfrac{{15}}{{14}}:\dfrac{{17}}{{11}} - \dfrac{6}{7}\) b) \(\left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 3}}{2}} \right):\dfrac{{17}}{{13}} + \left( {\dfrac{7}{2} + \dfrac{{ - 1}}{3}} \right):\dfrac{{17}}{{13}}\) c) \({3^2}.\dfrac{1}{{243}}{.81^2}.\dfrac{1}{{{3^3}}}\) d) \(\left( {{{4.2}^5}} \right):\left( {{2^3}.\dfrac{1}{{16}}} \right)\) Bài 2: (2,0 điểm) Tìm \(x\), biết: a) \(\left( { - 0,2} \right) - x.\dfrac{1}{6} = \dfrac{2}{3}\)b) \(\left( {\dfrac{1}{3}x - \dfrac{8}{{13}}} \right).\left( {2,5 + \dfrac{{ - 7}}{5}:x} \right) = 0\) c) \(5.\left( {\dfrac{1}{{\sqrt {25} }} - x} \right) - \sqrt {\dfrac{1}{{81}}} = \dfrac{{ - 1}}{9}\) d) \(\left| x \right| - \dfrac{{23}}{{17}} = 0\) Bài 3: (1,5 điểm) Một chiếc khay nhựa đựng đồ có dạng hình hộp chữ nhật như hình vẽ bên dưới.
Dựa vào kích thước trên hình (coi mép khay nhựa không đáng kể), hãy tỉnh: a) Diện tích xung quanh của chiếc khay. b) Diện tích nhựa để làm chiếc khay trên. c) Thể tích nước khay nhựa có thể chứa được. Bài 4: (1,0 điểm) Chi phí xây dựng nhà được biểu diễn qua biểu đồ hình quạt tròn sau:
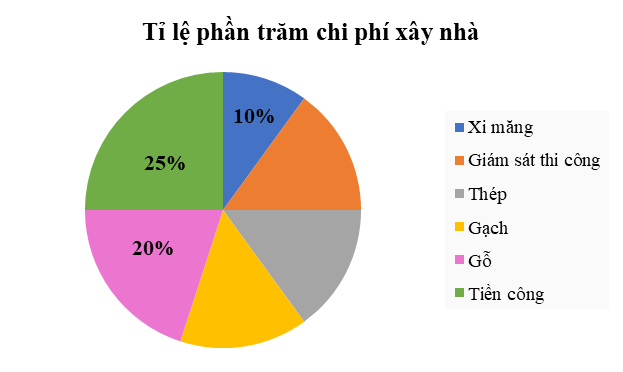
a) Tính số phần trăm chi phí gạch. Biết rằng chi phí giám sát thi công, thép, gạch bằng nhau. b) Biết rằng để xây dựng một ngôi nhà bác An đã chi trả hết 2,5 tỉ đồng. Hỏi chi phí trả tiền công là bao nhiêu? Bài 5: (0,5 điểm) Cho hai góc có cạnh tương ứng song song cùng nhọn hoặc cùng tù. Biết hai tia phân giác của chúng không cùng nằm trên một đường thẳng. Chứng minh rằng hai tia phân giác này song song với nhau. Lời giải Phần I: Trắc nghiệm
Câu 1 Phương pháp: Số hữu tỉ và số hữu tỉ được gọi chung là số thực. Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\,\) với \(a,b \in \mathbb{Z},b \ne 0\). Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ. Cách giải: + Mọi số vô tỉ đều là số thực là phát biểu đúng. + Mọi số thực đều là số vô tỉ là phát biểu sai. + Số 0 là số hữu tỉ là phát biểu đúng. + \( - \sqrt 2 \) là số vô tỉ là phát biểu đúng. Chọn B. Câu 2 Phương pháp: Diện tích của tam giác có cạnh là \(a\) và chiều cao tương ứng với cạnh đó là \(h\) được tính theo công thức \(S = \dfrac{1}{2}a.h\) Cách giải: Chiều cao của tam giác là: \(\dfrac{2}{9}:2 = \dfrac{2}{9}.\dfrac{1}{2} = \dfrac{1}{9}\,\left( m \right)\) Diện tích của tam giác là: \(\dfrac{1}{2}.\dfrac{2}{9}.\dfrac{1}{9} = \dfrac{1}{{81}}\,\left( {{m^2}} \right)\) Vậy diện tích của tam giác đã cho là \(\dfrac{1}{{81}}{m^2}\) Chọn D. Câu 3 Phương pháp: Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\) Cách giải: Ta có: \(6 = \sqrt {36} \) Vì \(36 > 34\) nên \(\sqrt {36} > \sqrt {34} \) suy ra \(\sqrt {36} - \sqrt {34} > 0\) hay \(6 - \sqrt {34} > 0\) Do đó, \(\left| {6 - \sqrt {34} } \right| = 6 - \sqrt {34} \) Ta có: \(\begin{array}{l}\left| {6 - \sqrt {34} } \right| + 3 + \sqrt {34} \\ = 6 - \sqrt {34} + 3 + \sqrt {34} \\ = \left( {6 + 3} \right) + \left( { - \sqrt {34} + \sqrt {34} } \right)\\ = 9 + 0\\ = 9\end{array}\) Chọn C. Câu 4 Phương pháp: Thực hiện phép nhân số hữu tỉ. Vận dụng quy tắc làm tròn số: Khi làm tròn một số thập phân đến hàng nào thì hàng đó gọi là hàng quy tròn. Muốn làm tròn số thập phân đến một hàng quy tròn nào đó, ta thực hiện các bước sau: - Gạch dưới chữ số thập phân của hàng quy tròn. - Nhìn sang chữ số ngay bên phải: + Nếu chữ số đó lớn hơn hoặc bằng 5 thì tăng chữ số gạch dưới lên một đơn vị rồi thay tất cả các chữ số bên phải bằng số 0 hoặc bỏ đi nếu chúng ở phần thập phân. + Nếu chữ số đó nhỏ hơn 5 thì giữ nguyên chữ số gạch chân dưới và thay tất cả các chữ số bên phải bằng số 0 hoặc bỏ đi nếu chúcng ở phần thập phân. Cách giải: Độ dài đường chéo của màn hình là: \(36.2,54 = 91,44\,\left( {cm} \right) \approx 91,4\,\left( {cm} \right)\) Chọn D. Câu 5 Phương pháp: Diện tích hình thoi có độ dài hai đường chéo lần lượt là \(a,b\) được tính theo công thức: \(S = \dfrac{{a.b}}{2}\) Thể tích hình lăng trụ đứng tứ giác có chiều cao \(h\) và diện tích đáy \(S\) được tính theo công thức: \(V = S.h\) Cách giải: Diện tích đáy của hình lăng trụ đó là: \(S = \dfrac{{18.30}}{2} = 270\,\left( {c{m^2}} \right)\) Thể tích của hình lăng trụ đó là: \(V = 270.20 = 5\,400\,\left( {c{m^3}} \right)\) Chọn A. Câu 6 Phương pháp: Hình lăng trụ đứng tam giác là hình hai mặt đáy là hình tam giác song song với nhau, ba mặt bên là các hình chữ nhật, các cạnh bên song song và bằng nhau. Hình lăng trụ đứng tứ giác là hình hai mặt đáy là hình tứ giác song song với nhau, bốn mặt bên là các hình chữ nhật, các cạnh bên song song và bằng nhau. Cách giải: Từ các hình đã cho, ta thấy: + Hình vẽ b), c) là hình lăng trụ đứng tứ giác. + Hình vẽ d) là hình lăng trụ đứng tam giác. Vậy hình vẽ b), c) và d) là các hình lăng trụ đứng tam giác hoặc lăng trụ đứng tứ giác. Chọn C. Câu 7 Phương pháp: Hai góc kề bù có tổng số đo góc bằng \({180^0}\) Vận dụng tính chất tia phân giác của một góc: \(Ot\) là tia phân giác của \(\angle xOy \Rightarrow \angle xOt = \angle yOt = \dfrac{1}{2}\angle xOy\) Cách giải: Theo giả thiết: \(\angle AOC - \angle BOC = {68^0} \Rightarrow \angle AOC = \angle BOC + {68^0}\) Vì \(\angle AOC\) và \(\angle BOC\) là hai góc kề bù nên \(\angle AOC + \angle BOC = {180^0}\) \(\begin{array}{l} \Rightarrow \angle BOC + {68^0} + \angle BOC = {180^0}\\ \Rightarrow 2\angle BOC = {180^0} - {68^0}\\ \Rightarrow 2\angle BOC = {112^0}\\ \Rightarrow \angle BOC = {112^0}:2\\ \Rightarrow \angle BOC = {56^0}\end{array}\) Vì \(Ot\) là tia phân giác của góc \(BOC\) nên \(\angle BOt = \dfrac{1}{2}\angle BOC\) (tính chất tia phân giác của một góc) \( \Rightarrow \angle BOt = \dfrac{1}{2}{.56^0} = {28^0}\) Vậy \(\angle BOt = {28^0}\) Chọn C. Câu 8 Phương pháp: Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song với nhau thì hai góc đồng vị bằng nhau. Hai góc kề bù có tổng số đo góc bằng \({180^0}\). Cách giải: *Ta có: \(m\) và \(n\) song song với nhau nên \(\angle mAB = \angle {B_3} = {80^0}\) (hai góc đồng vị) *Hai góc \({B_3}\) và góc \({B_4}\) kề bù với nhau nên \(\angle {B_3} + \angle {B_4} = {180^0}\) \(\begin{array}{l} \Rightarrow {80^0} + \angle {B_4} = {180^0}\\ \Rightarrow \angle {B_4} = {180^0} - {80^0} = {100^0}\end{array}\) Chọn B. Câu 9 Phương pháp: Ứng dụng của biểu đồ hình quạt tròn. Cách giải: Biểu đồ hình quạt tròn dùng để so sánh các thành phần trong toàn bộ dữ liệu. Chọn B. Câu 10 Phương pháp: Phân tích dữ liệu biểu đồ đoạn thẳng. Cách giải: Từ biểu đồ đoạn thẳng, ta thấy năm 2020, Việt Nam có mức thu nhập cao nhất là 2786 đô la/năm. Chọn D. Phần II. Tự luận: Bài 1 Phương pháp: a), b) Thực hiện phép cộng, trừ, nhân, chia với số hữu tỉ Vận dụng tính chất phân phối của phép nhân và phép cộng tính hợp lí c) Tích và thương của hai lũy thừa cùng cơ số: + Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: \({x^m}.{x^n} = {x^{m + n}}\) + Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: \({x^m}:{x^n} = {x^{m - n}}\,\left( {x \ne 0;m \ge n} \right)\) Lũy thừa của một lũy thừa: Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\) Cách giải: a) \(\dfrac{{ - 15}}{{14}}:\dfrac{{17}}{{23}} - \dfrac{{15}}{{14}}:\dfrac{{17}}{{11}} - \dfrac{6}{7}\) \(\begin{array}{l} = \dfrac{{ - 15}}{{14}}.\dfrac{{23}}{{17}} - \dfrac{{15}}{{14}}.\dfrac{{11}}{{17}} - \dfrac{6}{7}\\ = \dfrac{{ - 15}}{{14}}.\dfrac{{23}}{{17}} + \dfrac{{ - 15}}{{14}}.\dfrac{{11}}{{17}} - \dfrac{6}{7}\\ = \dfrac{{ - 15}}{{14}}.\left( {\dfrac{{23}}{{17}} + \dfrac{{11}}{{17}}} \right) - \dfrac{6}{7}\\ = \dfrac{{ - 15}}{{14}}.\dfrac{{34}}{{17}} - \dfrac{6}{7}\\ = \dfrac{{ - 15}}{{14}}.2 - \dfrac{6}{7}\\ = \dfrac{{ - 15}}{7} - \dfrac{6}{7}\\ = \dfrac{{ - 21}}{7} = - 3\end{array}\) b) \(\left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 3}}{2}} \right):\dfrac{{17}}{{13}} + \left( {\dfrac{7}{2} + \dfrac{{ - 1}}{3}} \right):\dfrac{{17}}{{13}}\) \(\begin{array}{l} = \left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 3}}{2}} \right).\dfrac{{13}}{{17}} + \left( {\dfrac{7}{2} + \dfrac{{ - 1}}{3}} \right).\dfrac{{13}}{{17}}\\ = \dfrac{{13}}{{17}}.\left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 3}}{2} + \dfrac{7}{2} + \dfrac{{ - 1}}{3}} \right)\\ = \dfrac{{13}}{{17}}.\left[ {\left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 1}}{3}} \right) + \left( {\dfrac{{ - 3}}{2} + \dfrac{7}{2}} \right)} \right]\\ = \dfrac{{13}}{{17}}.\left( {\dfrac{{ - 6}}{3} + \dfrac{4}{2}} \right)\\ = \dfrac{{13}}{{17}}.\left( { - 2 + 2} \right)\\ = \dfrac{{13}}{{17}}.0 = 0\end{array}\) c) \({3^2}.\dfrac{1}{{243}}{.81^2}.\dfrac{1}{{{3^3}}}\) \(\begin{array}{l} = {3^2}.\dfrac{1}{{{3^5}}}.{\left( {{3^4}} \right)^2}.\dfrac{1}{{{3^3}}}\\ = {3^2}.\dfrac{1}{{{3^5}}}{.3^8}.\dfrac{1}{{{3^3}}}\\ = \dfrac{{{3^2}{{.3}^8}}}{{{3^5}{{.3}^3}}} = \dfrac{{{3^{2 + 8}}}}{{{3^{5 + 3}}}}\\ = \dfrac{{{3^{10}}}}{{{3^8}}} = {3^{10 - 8}} = {3^2} = 9\end{array}\) d) \(\left( {{{4.2}^5}} \right):\left( {{2^3}.\dfrac{1}{{16}}} \right)\) \(\begin{array}{l} = \left( {{2^2}{{.2}^5}} \right):\left( {{2^3}.\dfrac{1}{{{2^4}}}} \right)\\ = {2^{2 + 5}}:\dfrac{{{2^3}}}{{{2^4}}} = {2^7}:\dfrac{1}{2}\\ = {2^7}.2 = {2^{7 + 1}}\\ = {2^8} = 256\end{array}\) Bài 2 Phương pháp: a) Vận dụng quy tắc chuyển vế tìm \(x\) b) \(A\left( x \right).B\left( x \right) = 0\) Trường hợp 1: Giải \(A\left( x \right) = 0\) Trường hợp 2: Giải \(B\left( x \right) = 0\) c) Tính căn bậc hai Vận dụng quy tắc chuyển vế tìm \(x\) d) \(\left| x \right| = a\) Trường hợp \(a < 0\), khi đó phương trình không có nghiệm \(x\) Trường hợp \(a > 0\), vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\) Cách giải:
a) \(\left( { - 0,2} \right) - x.\dfrac{1}{6} = \dfrac{2}{3}\) \(\begin{array}{l}\dfrac{{ - 1}}{5} - x.\dfrac{1}{6} = \dfrac{2}{3}\\ - x.\dfrac{1}{6} = \dfrac{2}{3} - \dfrac{{ - 1}}{5}\\ - x.\dfrac{1}{6} = \dfrac{{10}}{{15}} + \dfrac{3}{{15}}\\ - x.\dfrac{1}{6} = \dfrac{{13}}{{15}}\\ - x = \dfrac{{13}}{{15}}:\dfrac{1}{6} = \dfrac{{13}}{{15}}.6\\ - x = \dfrac{{26}}{5}\\x = \dfrac{{ - 26}}{5}\end{array}\) Vậy \(x = \dfrac{{ - 26}}{5}\) b) \(\left( {\dfrac{1}{3}x - \dfrac{8}{{13}}} \right).\left( {2,5 + \dfrac{{ - 7}}{5}:x} \right) = 0\) Trường hợp 1: \(\begin{array}{l}\dfrac{1}{3}x - \dfrac{8}{{13}} = 0\\\dfrac{1}{3}x = \dfrac{8}{{13}}\\x = \dfrac{8}{{13}}:\dfrac{1}{3}\\x = \dfrac{8}{{13}}.3\\x = \dfrac{{24}}{{13}}\end{array}\) Trường hợp 2: \(\begin{array}{l}2,5 + \dfrac{{ - 7}}{5}:x = 0\\\dfrac{{ - 7}}{5}:x = - 2,5\\x = \dfrac{{ - 7}}{5}:\left( { - 2,5} \right) = \dfrac{{ - 7}}{5}:\dfrac{{\left( { - 5} \right)}}{2}\\x = \dfrac{{ - 7}}{5}.\dfrac{2}{{\left( { - 5} \right)}}\\x = \dfrac{{14}}{{25}}\end{array}\) Vậy \(x \in \left\{ {\dfrac{{24}}{{13}};\dfrac{{14}}{{25}}} \right\}\) c) \(5.\left( {\dfrac{1}{{\sqrt {25} }} - x} \right) - \sqrt {\dfrac{1}{{81}}} = \dfrac{{ - 1}}{9}\) \(\begin{array}{l}5.\left( {\dfrac{1}{5} - x} \right) - \dfrac{1}{9} = \dfrac{{ - 1}}{9}\\5.\left( {\dfrac{1}{5} - x} \right) = \dfrac{{ - 1}}{9} + \dfrac{1}{9}\\5.\left( {\dfrac{1}{5} - x} \right) = 0\\\dfrac{1}{5} - x = 0\\x = \dfrac{1}{5}\end{array}\) Vậy \(x = \dfrac{1}{5}\) d) \(\begin{array}{l}\left| x \right| - \dfrac{{23}}{{17}} = 0\\\left| x \right| = \dfrac{{23}}{{17}}\end{array}\) \(\left[ {\begin{array}{*{20}{c}}{x = \dfrac{{23}}{{17}}}\\{x = \dfrac{{ - 23}}{{17}}}\end{array}} \right.\) Vậy \(x \in \left\{ {\dfrac{{23}}{{17}};\dfrac{{ - 23}}{{17}}} \right\}\) Bài 3 Phương pháp: a) Diện tích xung quanh của hình hộp chữ nhật có ba kích thước chiều dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c\) được tính theo công thức: \({S_{xq}} = 2.\left( {a + b} \right).c\) b) Thể tích của hình hộp chữ nhật có ba kích thước chiều dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c\) được tính theo công thức: \(V = abc\) Cách giải: a) Diện tích xung quanh của chiếc khay nhựa dạng hình hộp chữ nhật là: \(2.\left( {27 + 20} \right).10 = 940\,\left( {c{m^2}} \right)\) b) Diện tích nhựa làm chiếc khay bằng tổng diện tích của các mặt xung quanh và mặt đáy. Diện tích mặt đáy của chiếc khay là: \(27.20 = 540\,\left( {c{m^2}} \right)\) Diện tích nhựa để làm chiếc khay là: \(940 + 540 = 1\,480\,\left( {c{m^2}} \right)\) c) Thể tích nước khay nhựa có thể chứa được là: \(20.27.10 = 5\,400\,\left( {c{m^3}} \right)\) Bài 4 Phương pháp: a) Gọi tỉ lệ phần trăm chi phí gạch là \(x\% \) (điều kiện: \(x > 0\)) Từ hình quạt tròn biểu diễn 100%, từ đó tìm được \(x\) b) Chi phí bác An trả tiền công = toàn bộ số tiền chi trả . % chi phí tiền công biểu diễn trên biểu đồ. Cách giải: a) Gọi tỉ lệ phần trăm chi phí gạch là \(x\% \) (điều kiện: \(x > 0\)) Vì chi phí giám sát thi công, thép, gạch bằng nhau nên tỉ lệ phần trăm của chi phí giám sát thi công, thép là \(x\% \) Ta có: \(\begin{array}{l}x + x + x + 20\% + 25\% + 10\% = 100\% \\3x + 55\% = 100\% \\3x = 100\% - 55\% \\3x = 45\% \\x = 45\% :3\\x = 15\% \end{array}\) Vậy chi phí trả tiền gạch chiếm \(15\% \). b) Chi phí bác An trả tiền công là: \(2,5.25\% = \dfrac{{25}}{{10}}.\dfrac{{25}}{{100}} = \dfrac{5}{8} = 0,625\)(tỉ) \( = 625\) (triệu đồng) Bài 5 Phương pháp: Vận dụng tính chất tia phân giác của một góc Vận dụng dấu hiệu nhận biết hai đường thẳng song song Cách giải:
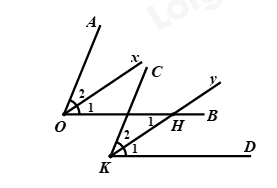
Hai \(\angle AOB\) và \(\angle CKD\) là hai góc có cạnh tương ứng song song cùng nhọn hoặc cùng tù nên \(\angle AOB = \angle CKD\) (1) Vì \(Ox\) là tia phân giác của góc \(\angle AOB\) nên \(\angle {O_1} = \dfrac{1}{2}\angle AOB\) (2) \(Ky\) là tia phân giác của góc \(\angle CKD\) nên \(\angle {K_1} = \dfrac{1}{2}\angle CKD\) (3) Từ (1), (2) và (3) suy ra \(\angle {O_1} = \angle {K_1}\) Mặt khác, vì \(OB//K{\rm{D}}\) nên \(\angle {H_1} = \angle {K_1}\) (so le trong) Do đó, \(\angle {O_1} = \angle {H_1}\left( { = \angle {K_1}} \right)\). Mà hai góc \(\angle {O_1};\angle {H_1}\) ở vị trí so le trong Do đó \(Ox//Ky\) (dấu hiệu nhận biết hai đường thẳng song song)
|