Lý thuyết Tỉ lệ thức - Dãy tỉ số bằng nhau Toán 7 Chân trời sáng tạo

I. Các kiến thức cần nhớ

1. Tỉ lệ thức

Ví dụ: $\dfrac{{28}}{{24}} = \dfrac{7}{6};$$\dfrac{3}{{10}} = \dfrac{{2,1}}{7}$

Ví dụ: Ta có $\dfrac{3}{6} = \dfrac{9}{{18}} \Rightarrow 3.18 = 9.6\left( { = 54} \right)$

Vì $4.9 = 3.12(=36)$ nên ta có các tỉ lệ thức sau: $\dfrac{4}{3} = \dfrac{{12}}{9};\,\dfrac{3}{4} = \dfrac{9}{{12}};\dfrac{4}{{12}} = \dfrac{3}{9};\dfrac{{12}}{4} = \dfrac{9}{3}$ 

Chú ý:

Khi nói các số $x,\,y,\,z$ tỉ lệ với các số $a,\,b,\,c$ tức là ta có $\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c}$. Ta cũng viết $x:y:z = a:b:c$

II. Các dạng toán thường gặp

Dạng 1: Lập tỉ lệ thức từ đẳng thức cho trước

Phương pháp:

Ta sử dụng: Nếu  $a.d = b.c$ thì

$\dfrac{a}{b} = \dfrac{c}{d}$; $\dfrac{a}{c} = \dfrac{b}{d}$; $\dfrac{d}{b} = \dfrac{c}{a};$ $\dfrac{d}{c} = \dfrac{b}{a}.$

Dạng 2: Tìm x, y

Phương pháp:

Sử dụng tính chất cơ bản của tỉ lệ thức: Nếu $\dfrac{a}{b} = \dfrac{c}{d}$ thì $a.d = b.c$

Trong một tỉ lệ thức ta có thể tìm một số hạng chưa biết khi biết ba số hạng còn lại.

$\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow a = \dfrac{{bc}}{d};\,b = \dfrac{{ad}}{c};$$c = \dfrac{{ad}}{b};\,d = \dfrac{{bc}}{a}$ .

Ví dụ:  Tìm x biết $\dfrac{x}{2} = \dfrac{8}{6}$

Ta có: 

$\begin{array}{l} \dfrac{x}{2} = \dfrac{8}{6}\\ \Rightarrow x.6 = 8.2\\ \Rightarrow x = \dfrac{{16}}{6}\\ \Rightarrow x = \dfrac{8}{3} \end{array}$

Dạng 3: Chứng minh các tỉ lệ thức

Phương pháp:

Dựa vào các tính chất của tỉ lệ thức và biến đổi linh hoạt để chứng minh.

Dạng 4: Tìm hai số $x;y$ biết tổng (hoặc hiệu) và tỉ số của chúng.

Phương pháp giải:

* Để tìm hai số $x;y$ khi biết tổng $x + y = s$ và tỉ số $\dfrac{x}{y} = \dfrac{a}{b}$ ta làm như sau

Ta có $\dfrac{x}{y} = \dfrac{a}{b} \Rightarrow \dfrac{x}{a} = \dfrac{y}{b}$

Áp dụng dãy tỉ số bằng nhau ta có :

$\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x + y}}{{a + b}} = \dfrac{s}{{a + b}}$

Từ đó $x = \dfrac{s}{{a + b}}.a;\,y = \dfrac{s}{{a + b}}.b$ .

* Để tìm hai số $x;y$ khi biết hiệu $x - y = p$ và tỉ số $\dfrac{x}{y} = \dfrac{a}{b}$ ta làm như sau

Ta có $\dfrac{x}{y} = \dfrac{a}{b}$$\Rightarrow \dfrac{x}{a} = \dfrac{y}{b}$

Áp dụng dãy tỉ số bằng nhau ta có :

$\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x - y}}{{a - b}} = \dfrac{p}{{a - b}}$

Từ đó $x = \dfrac{p}{{a - b}}.a;$$y = \dfrac{p}{{a - b}}.b$ .

Ví dụ: Tìm hai số $x;y$ biết $\frac{x}{3} = \frac{y}{5}$ và $x + y =  - 32$

Áp dụng dãy tỉ số bằng nhau ta có:

$\frac{x}{3} = \frac{y}{5} = \frac{{x + y}}{{3 + 5}} = \frac{{ - 32}}{8} =  - 4$

Do đó $\frac{x}{3} =  - 4 \Rightarrow x = (-4).3 = - 12$  và $\frac{y}{5} =  - 4 \Rightarrow y = (-4).5 = - 20.$

Vậy $x =  - 12;y =  - 20.$

Dạng 5: Chia một số thành các phần tỉ lệ với các số cho trước

Phương pháp:

Giả sử chia số $P$ thành ba phần $x,\,y,\,z$ tỉ lệ với các số $a,b,c$, ta làm như sau:

$\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{{x + y + z}}{{a + b + c}} = \dfrac{P}{{a + b + c}}$

Từ đó $x = \dfrac{P}{{a + b + c}}.a;\,y = \dfrac{P}{{a + b + c}}.b$; $z = \dfrac{P}{{a + b + c}}.c$.

Dạng 6: Tìm hai số biết tổng và tỉ số của chúng

Phương pháp:

Tìm hai số $x;\,y$ biết $x.y = P$ và $\dfrac{x}{y} = \dfrac{a}{b}$

Cách 1: Ta có $\dfrac{x}{y} = \dfrac{a}{b} \Rightarrow \dfrac{x}{a} = \dfrac{y}{b}$

Đặt $\dfrac{x}{a} = \dfrac{y}{b} = k$ ta có $x = ka;\,y = kb$

Nên $x.y = ka.kb = {k^2}ab = P$$\Rightarrow {k^2} = \dfrac{P}{{ab}}$

Từ đó tìm được $k$ sau đó tìm được $x,y$.

Cách 2: Ta có $\dfrac{x}{y} = \dfrac{a}{b}$$\Rightarrow \dfrac{{{x^2}}}{{xy}} = \dfrac{a}{b}$ hay $\dfrac{{{x^2}}}{P} = \dfrac{a}{b}$$\Rightarrow {x^2} = \dfrac{{Pa}}{b}$  từ đó tìm được $x$ và $y.$

Dạng 7: Chứng minh đẳng thức từ một tỉ lệ thức cho trước.

Phương pháp:

Áp dụng tính chất tỉ lệ thức và tính chất dãy tỉ số bằng nhau.

Dạng 8: Bài toán về tỉ lệ thức

Phương pháp:

+ Xác định mối quan hệ giữa các yếu tố của đề bài

+ Lập được tỉ lệ thức

+ Áp dụng tính chất dãy tỉ số bằng nhau để giải bài toán.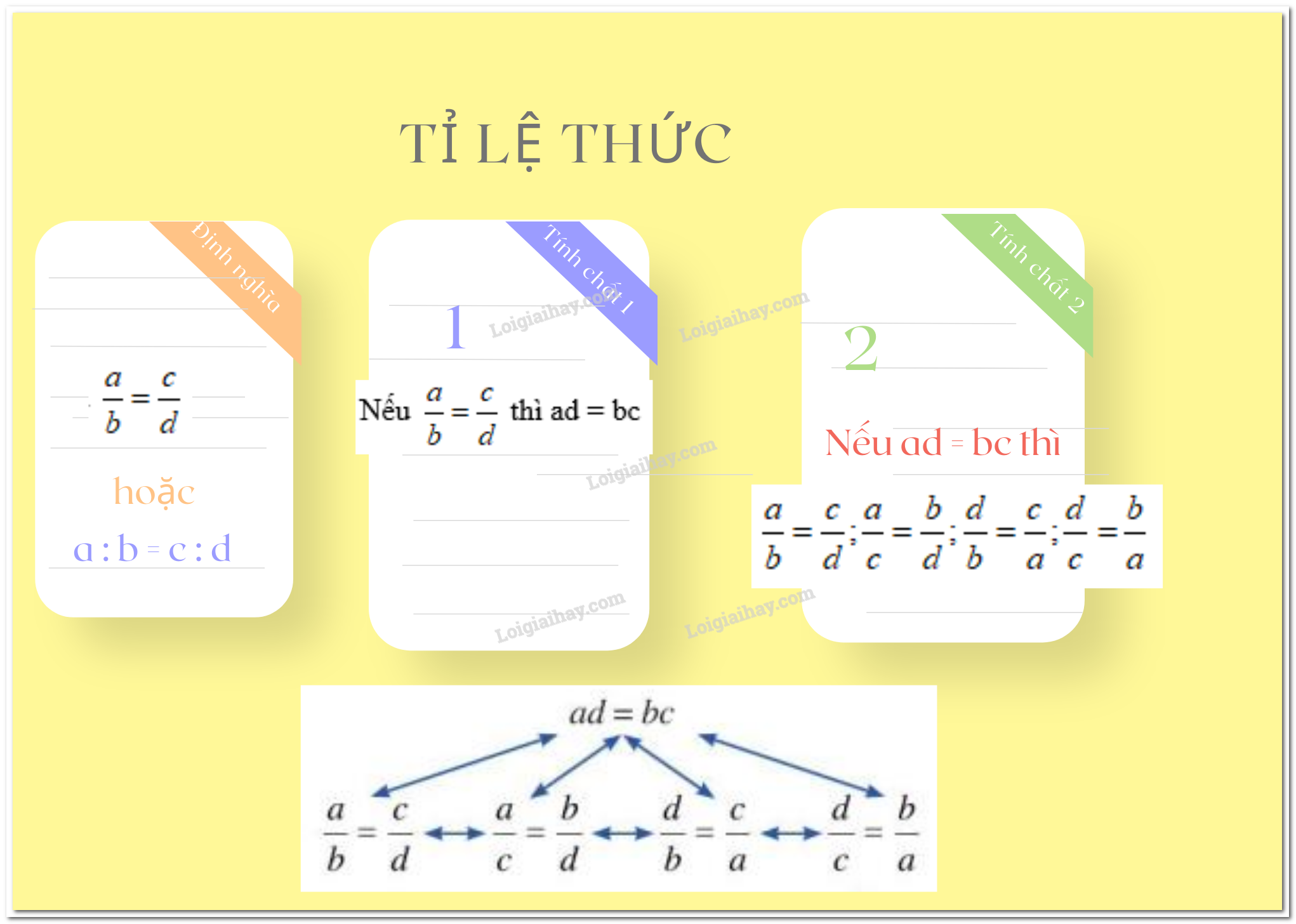