Trắc nghiệm Bài 38: Hình chóp tam giác đều Toán 8 Kết nối tri thứcĐề bài
Câu 1 :
Các mặt bên của hình chóp tam giác đều là hình gì?
Câu 2 :
Đường cao của hình chóp tam giác đều là?
Câu 3 :
Diện tích xung quanh của hình chóp tam giác đều bằng:
Câu 4 :
Cho hình chóp tam giác đều có diện tích đáy S, chiều cao h. Khi đó thể tích V của hình chóp được tính bằng công thức:
Câu 5 :
Trung đoạn của hình chóp tam giác đều S.ABC là:
Câu 6 :
Cho hình chóp tam giác đều có diện tích đáy là \(6c{m^2}\), chiều cao của hình chóp là \(8cm\). Tính thể tích của hình chóp đó.
Câu 7 :
Cho khối chóp tam giác đều, nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể tích của khối chóp sẽ:
Câu 8 :
Cho hình chóp tam giác đều S.ABC có các mặt là các tam giác đều. Biết diện tích của mặt đáy bằng \(10c{m^2}\). Tính diện tích xung quanh hình chóp.
Câu 9 :
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy là 4cm, độ dài trung đoạn bằng 5cm. Tính diện tích xung quanh hình chóp.
Câu 10 :
Cho hình chóp tam giác đều chiều cao h, thể tích V. Diện tích đáy S bằng:
Câu 11 :
Hình chóp tam giác đều có mấy mặt:
Câu 13 :
Số đo mỗi góc ở đỉnh của mặt đáy hình chóp tam giác đều là?
Câu 14 :
Cho hình chóp tam giác đều S.ABC biết SA = 4cm, AB = 3cm, chọn phát biểu đúng?
Câu 15 :
Cho hình chóp tam giác đều có nửa chu vi đáy là \(12cm\), độ dài trung đoạn là \(4cm\). Tính diện tích xung quanh của hình chóp đó.
Câu 16 :
Cho hình chóp tam giác đều S. ABC có diện tích đáy là 5, chiều cao h của hình chóp có số đo bằng số đo cạnh của hình vuông có diện tích \(\frac{9}{4}c{m^2}\). Thể tích của khối chóp đó là bao nhiêu?
Câu 17 :
Cho hình chóp tam giác đều S.ABC có chu vi đáy bằng 9cm, chiều cao mặt đáy bằng \(\frac{{3\sqrt 3 }}{2}cm\), chiều cao hình chóp bằng \(\frac{3}{2}\)độ dài cạnh đáy. Thể tích V của khối chóp S.ABC.
Câu 18 :
Cho hình chóp tam giác đều S.ABC có H là trọng tâm mặt đáy ABC, biết chiều cao hình chóp SH = a, độ dài \(AH = \frac{{a\sqrt 3 }}{3}\), cạnh đáy có độ dài bằng a. Thể tích V của khối chóp S.ABC theo a.
Câu 19 :
Cho hình chóp tam giác đều S.ABC có độ dài tất cả các cạnh bằng 4cm. Gọi I. H lần lượt là trung điểm cạnh AB, SC. Tính độ dài IH
Câu 20 :
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I là trung điểm cạnh BC. Tính thể tích V của khối chóp S.ABI.
Câu 21 :
Chọn phát biểu sai trong các phát biểu sau:
Câu 22 :
Một hình chóp tam giác đều có thể tích bằng \(8\sqrt 3 c{m^3}\), chiều cao bằng 6cm. Tính độ dài cạnh đáy.
Câu 23 :
Cho hình chóp tam giác đều nằm trong một lăng trụ đứng đáy là tam giác đều như hình, Biết diện tích xung quanh của lăng trụ đứng bằng \(36c{m^2}\), chiều cao mặt đáy bằng \(2\sqrt 3 cm\), cạnh đáy bằng 4cm. Tính thể tích hình chóp tam giác đều.
Câu 25 :
Cho hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau, chiều cao mặt đáy bằng \(3\sqrt 3 cm\). Tính chiều cao mặt bên hình chóp.
Lời giải và đáp án
Câu 1 :
Các mặt bên của hình chóp tam giác đều là hình gì?
Câu 2 :
Đường cao của hình chóp tam giác đều là?
Đáp án : B Phương pháp giải :
Sử dụng định nghĩa đường cao của hình chóp tam giác đều: Đoạn thẳng nối đỉnh của hình chóp và trọng tâm của tam giác đáy gọi là đường cao của hình chóp tam giác đều Lời giải chi tiết :
Theo định nghĩa đường cao của hình chóp tam giác đều thì đường cao là đoạn thẳng kẻ từ đỉnh tới trọng tâm của mặt đáy nên chọn đáp án B
Câu 3 :
Diện tích xung quanh của hình chóp tam giác đều bằng:
Đáp án : C Phương pháp giải :
Sử dụng công thức tính diện tích xung quanh của hình chóp tam giác đều Lời giải chi tiết :
Diện tích xung quanh của hình chóp tam giác đều bằng tích của nửa chu vi đáy với trung đoạn nên chọn đáp án C
Câu 4 :
Cho hình chóp tam giác đều có diện tích đáy S, chiều cao h. Khi đó thể tích V của hình chóp được tính bằng công thức:
Đáp án : D Phương pháp giải :
Sử dụng công thức tính thể tích của hình chóp tam giác đều. Lời giải chi tiết :
Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó nên chọn đáp án D
Câu 5 :
Trung đoạn của hình chóp tam giác đều S.ABC là:
Đáp án : A Phương pháp giải :
Sử dụng định nghĩa trung đoạn của hình chóp tam giác đều: Đường cao kẻ từ đỉnh của mỗi mặt bên gọi là trung đoạn của hình chóp tam giác đều Lời giải chi tiết :
Theo định nghĩa trung đoạn của hình chóp tam giác đều thì chọn đáp án A
Câu 6 :
Cho hình chóp tam giác đều có diện tích đáy là \(6c{m^2}\), chiều cao của hình chóp là \(8cm\). Tính thể tích của hình chóp đó.
Đáp án : C Phương pháp giải :
Sử dụng công thức thể tích của hình chóp tam giác đều: \(V = \frac{1}{3}.S.h\) Lời giải chi tiết :
Theo công thức thể tích của hình chóp tam giác đều: \(V = \frac{1}{3}.S.h = \frac{1}{3}.6.8 = 16c{m^3}\)
Câu 7 :
Cho khối chóp tam giác đều, nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể tích của khối chóp sẽ:
Đáp án : D Phương pháp giải :
Dựa vào công thức tính thể tích khối chóp Lời giải chi tiết :
Nếu cạnh đáy tăng lên 2 lần thì diện tích đáy tăng 4 lần. Vì chiều cao giảm đi 4 lần nên thể tích khối chóp không thay đổi. Ví dụ: Hình chóp tam giác đều S.ABC có cạnh đáy là a, chiều cao là h. Vì tam giác ABC đều nên chiều cao của tam giác ABC là: \(\sqrt{a^2 - \left(\frac{a}{2}\right)^2} = \frac{a\sqrt3}{2}\) Suy ra \(V_{S.ABC} = \frac{1}{3}.h.\frac{1}{2}.a.\frac{a\sqrt3}{2} = \frac{\sqrt3a^2h}{12}\) Sau khi tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần ta được hình chóp mới S.A'B'C' Cạnh đáy tăng lên 2 lần thì đáy mới là a' = 2a, khi đó chiều cao của tam giác A'B'C' là: \(\sqrt{(2a)^2 - \left(\frac{2a}{2}\right)^2} = a\sqrt3\) Vì chiều cao h giảm đi 4 lần nên chiều cao mới là \(h' = \frac{h}{4}\) \(V_{S.A'B'C'} = \frac{1}{3}.h'.S_{A'B'C'}\) \(= \frac{1}{3}.\frac{h}{4}.\frac{1}{2}.(2a).a\sqrt3\) \(= \frac{\sqrt3a^2h}{12}\) Vậy nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi bốn lần thì thể tích của khối chóp sẽ không thay đổi
Câu 8 :
Cho hình chóp tam giác đều S.ABC có các mặt là các tam giác đều. Biết diện tích của mặt đáy bằng \(10c{m^2}\). Tính diện tích xung quanh hình chóp.
Đáp án : D Phương pháp giải :
Dựa vào đặc điểm của hình chóp tam giác đều. Lời giải chi tiết :
Hình chóp S.ABC là hình chóp tam giác đều, các mặt là các tam giác đều nên diện tích các mặt bằng nhau và cùng bằng\(10c{m^2}\). Vậy diện tích xung quanh của hình chóp S.ABC là \(3.10 = 30c{m^2}\)
Câu 9 :
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy là 4cm, độ dài trung đoạn bằng 5cm. Tính diện tích xung quanh hình chóp.
Đáp án : C Phương pháp giải :
Dựa vào công thức tính diện tích xung quanh của hình chóp. Lời giải chi tiết :
Nửa chu vi đáy của hình chóp: \(p = \frac{{4 + 4 + 4}}{2} = 6cm\) Vậy diện tích xung quanh của hình chóp S.ABC là \({S_{xq}} = p.d = 6.5 = 30c{m^2}\).
Câu 10 :
Cho hình chóp tam giác đều chiều cao h, thể tích V. Diện tích đáy S bằng:
Đáp án : D Phương pháp giải :
Dựa vào công thức tính thể tích của hình chóp đều. Lời giải chi tiết :
\(V = \frac{1}{3}.S.h \Rightarrow S = \frac{{3V}}{h}\)
Câu 11 :
Hình chóp tam giác đều có mấy mặt:
Đáp án : B Phương pháp giải :
Quan sát hình chóp tam giác đều đếm số mặt. Lời giải chi tiết :
Hình chóp tam giác đều có 4 mặt nên chọn đáp án B
Đáp án : A Phương pháp giải :
Sử dụng định nghĩa trung đoạn của hình chóp tam giác đều: Đường cao kẻ từ đỉnh của mỗi mặt bên gọi là trung đoạn của hình chóp tam giác đều Lời giải chi tiết :
Theo định nghĩa trung đoạn của hình chóp tam giác đều thì trung đoạn của hình chóp S.ABC là đoạn SH nên chọn đáp án A
Câu 13 :
Số đo mỗi góc ở đỉnh của mặt đáy hình chóp tam giác đều là?
Đáp án : C Phương pháp giải :
Sử dụng kiến thức đáy của hình chóp tam giác đều là tam giác đều. Lời giải chi tiết :
Vì đáy của hình chóp tam giác đều là tam giác đều, mà mỗi góc của tam giác đều có số đo bằng \({60^0}\) nên chọn đáp án C
Câu 14 :
Cho hình chóp tam giác đều S.ABC biết SA = 4cm, AB = 3cm, chọn phát biểu đúng?
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về các cạnh của hình chóp tam giác đều: Hình chóp tam giác đều có đáy là tam giác đều, các mặt bên là các tam giác cân bằng nhau có chung đỉnh. Lời giải chi tiết :
Hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều nên \(AC = BC = AB = 3cm\) Hình chóp tam giác đều có các mặt bên là các tam giác cân bằng nhau có chung đỉnh nên \(SB = SC = SA = 4cm\). nên chọn đáp án B đúng
Câu 15 :
Cho hình chóp tam giác đều có nửa chu vi đáy là \(12cm\), độ dài trung đoạn là \(4cm\). Tính diện tích xung quanh của hình chóp đó.
Đáp án : A Phương pháp giải :
Sử dụng công thức tính diện tích xung quanh của hình chóp tam giác đều: \({S_{xq}} = p.d\) Lời giải chi tiết :
Theo công thức tính diện tích xung quanh của hình chóp tam giác đều: \({S_{xq}} = p.d = 12.4 = 48c{m^2}\)
Câu 16 :
Cho hình chóp tam giác đều S. ABC có diện tích đáy là 5, chiều cao h của hình chóp có số đo bằng số đo cạnh của hình vuông có diện tích \(\frac{9}{4}c{m^2}\). Thể tích của khối chóp đó là bao nhiêu?
Đáp án : D Phương pháp giải :
B1: Tính cạnh của hình vuông từ đó suy ra chiều cao h của hình chóp. B2. Áp dụng công thức thể tích khối chóp \(V = \frac{1}{3}.S.h\) Lời giải chi tiết :
Vì \(\frac{9}{4} = \frac{3}{2}.\frac{3}{2}\) nên cạnh của hình vuông bằng \(\frac{3}{2}cm\) Chiều cao hình chóp có số đo bằng số đo cạnh của hình vuông có diện tích \(\frac{9}{4}c{m^2}\)nên \(h = \frac{3}{2}cm\). Áp dụng công thức thể tích khối chóp ta được: \(V = \frac{1}{3}.S.h = \frac{1}{3}.5.\frac{3}{2} = \frac{5}{2}(c{m^3})\)
Câu 17 :
Cho hình chóp tam giác đều S.ABC có chu vi đáy bằng 9cm, chiều cao mặt đáy bằng \(\frac{{3\sqrt 3 }}{2}cm\), chiều cao hình chóp bằng \(\frac{3}{2}\)độ dài cạnh đáy. Thể tích V của khối chóp S.ABC.
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về hình chóp đều, chu vi tam giác để tính. B1: Tính độ dài cạnh đáy dựa vào chu vi. B2: Tính chiều cao hình chóp dựa vào điều kiện đề bài. B3: Tính diện tích mặt đáy. B4: Tính thể tích hình chóp theo công thức. Lời giải chi tiết :
Tam giác ABC đều nên \(AB = BC = CA\) Vì chu vi tam giác ABC bằng 9cm nên \(AB + BC + CA = 9\) \(\begin{array}{l} \Rightarrow 3.BC = 9\\ \Rightarrow BC = 3(cm)\end{array}\) Gọi H là trọng tâm tam giác ABC, M là trung điểm BC. Khi đó SH là chiều cao của hình chóp \( \Rightarrow SH = \frac{3}{2}.BC = \frac{3}{2}.3 = \frac{9}{2}(cm)\) AM là trung tuyến của tam giác đều ABC nên AM đồng thời là đường cao của đáy\( \Rightarrow AM = \frac{{3\sqrt 3 }}{2}(cm)\) \({S_{ABC}} = \frac{1}{2}.BC.AM = \frac{1}{2}.3.\frac{{3\sqrt 3 }}{2} = \frac{{9\sqrt 3 }}{4}(c{m^2})\) \({V_{ABC}} = \frac{1}{3}.{S_{ABC}}.SH = \frac{1}{3}.\frac{{9\sqrt 3 }}{4}.\frac{9}{2} = \frac{{27\sqrt 3 }}{8}(c{m^3})\)
Câu 18 :
Cho hình chóp tam giác đều S.ABC có H là trọng tâm mặt đáy ABC, biết chiều cao hình chóp SH = a, độ dài \(AH = \frac{{a\sqrt 3 }}{3}\), cạnh đáy có độ dài bằng a. Thể tích V của khối chóp S.ABC theo a.
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về hình chóp đều, tính chất đường trung tuyến của tam giác. B1: Tính chiều cao của cạnh đáy. B2: Tính diện tích đáy tam giác. B3: Áp dụng công thức tính thể tích hình chóp đều để tính. Lời giải chi tiết :
Gọi x là độ dài một cạnh của hình chóp.
H là trọng tâm tam giác đều ABC, áp dụng tính chất đường trung tuyến trong tam giác ta được: \(AH = \frac{2}{3}.AM \Rightarrow AM = \frac{{a\sqrt 3 }}{3}:\frac{2}{3} = \frac{{a\sqrt 3 }}{2}\) Tam giác ABC đều nên diện tích đáy bằng: \(S = \frac{1}{2}.BC.AH = \frac{1}{2}.a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{4}\) \(V = \frac{1}{3}.S.h = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{{12}}\)
Câu 19 :
Cho hình chóp tam giác đều S.ABC có độ dài tất cả các cạnh bằng 4cm. Gọi I. H lần lượt là trung điểm cạnh AB, SC. Tính độ dài IH
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về hình chóp đều, định lý Pythagore và diện tích tam giác đều để tính. Lời giải chi tiết :
\(AI = IB = \frac{{AB}}{2} = 2cm\) \(SH = HC = \frac{{SC}}{2} = \frac{4}{2} = 2cm\) Tam giác ABC dều cạnh a nên CI là trung tuyến đồng thời là đường cao của tam giác ABC . Áp dụng định lý Pythagore cho tam giác vuông CIA có \(\begin{array}{l}C{I^2} + I{A^2} = A{C^2}\\ = > C{I^2} = A{C^2} - I{A^2}\\ = > C{I^2} = {4^2} - {2^2}\\ = > CI = 2\sqrt 3 cm\end{array}\) Tương tự áp dụng định lí Pythagore cho tam giác vuông SIB ta được: \(SI = 2\sqrt 3 cm\) Xét tam giác SIC có: \(SI = IC = 2\sqrt 3 cm\) \( \Rightarrow \)Tam giác SIC cân tại I \( \Rightarrow \) IH vừa là trung tuyến đồng thời là đường cao của tam giác SIC cân. Áp dụng định lý Pythagore cho tam giác vuông SIH có \(\begin{array}{l}C{I^2} = I{H^2} + C{H^2}\\ = > I{H^2} = C{I^2} - C{H^2}\\ = > I{H^2} = {(2\sqrt 3 )^2} - {2^2}\\ = > IH = 2\sqrt 2 cm\end{array}\)
Câu 20 :
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I là trung điểm cạnh BC. Tính thể tích V của khối chóp S.ABI.
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về hình chóp đều, định lý Pythagore và diện tích tam giác đều để tính. Lời giải chi tiết :
Gọi O là trọng tâm tam giác ABC đều. Khi đó SO là chiều cao của hình chóp SABC đồng thời là chiều cao của hình chóp S.ABI \(AO = \frac{2}{3}.AI = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\) \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{{(2a)}^2} - {{(\frac{{a\sqrt 3 }}{3})}^2}} = \frac{{a\sqrt {33} }}{3}\) Tam giác ABC đều cạnh a nên diện tích tam giác bằng: \({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\) \({V_{ABC}} = \frac{1}{3}.{S_{ABC}}.SO = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt {33} }}{3} = \frac{{{a^3}\sqrt {11} }}{{12}}\) \(\frac{{{V_{ABI}}}}{{{V_{ABC}}}} = \frac{{\frac{1}{3}.{S_{ABI}}.SO}}{{\frac{1}{3}.{S_{ABC}}.SO}} = \frac{{{S_{ABI}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}.AI.BI}}{{\frac{1}{2}.AI.BA}} = \frac{{BI}}{{BA}} = \frac{1}{2} = > {V_{ABI}} = \frac{1}{2}{V_{ABC}} = \frac{1}{2}.\frac{{{a^3}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{8}\)
Câu 21 :
Chọn phát biểu sai trong các phát biểu sau:
Đáp án : A Phương pháp giải :
Dựa vào khái niệm hình chóp tam giác đều, đường cao, trung đoạn, công thức tính diện tích xung quanh của hình chóp đều. Lời giải chi tiết :
Hình chóp tam giác đều có đáy là tam giác đều, các mặt bên là các tam giác cân bằng nhau có chung đỉnh nên câu A sai Đoạn thẳng nối đỉnh của hình chóp và trọng tâm của tam giác đáy gọi là đường cao của hình chóp tam giác đều nên câu B đúng Đường cao kẻ từ đỉnh của mỗi mặt bên gọi là trung đoạn của hình chóp tam giác đều nên câu C đúng Diện tích xung quanh của hình chóp tam giác đều bằng tích của nửa chu vi đáy với trung đoạn nên câu D đúng
Câu 22 :
Một hình chóp tam giác đều có thể tích bằng \(8\sqrt 3 c{m^3}\), chiều cao bằng 6cm. Tính độ dài cạnh đáy.
Đáp án : B Phương pháp giải :
B1: Tính diện tích đáy. B2: Gọi x là độ dài cạnh đáy , tính chiều cao mặt đáy theo x. B3: Tìm x. Lời giải chi tiết :
Diện tích đáy của hình chóp là : \(8\sqrt 3 .3:6 = 4\sqrt 3 c{m^2}\) Gọi x là độ dài cạnh đáy, vì đáy hình chóp tam giác đều là một tam giác đều nên chiều cao của hình chóp là \(\frac{{x\sqrt 3 }}{2}\) Khi đó diện tích đáy tính theo x là \(\frac{1}{2}.x.\frac{{x\sqrt 3 }}{2} = \frac{{{x^2}\sqrt 3 }}{4} \Rightarrow \frac{{{x^2}\sqrt 3 }}{4} = 4\sqrt 3 \Rightarrow {x^2} = 16 \Rightarrow x = 4cm\)
Câu 23 :
Cho hình chóp tam giác đều nằm trong một lăng trụ đứng đáy là tam giác đều như hình, Biết diện tích xung quanh của lăng trụ đứng bằng \(36c{m^2}\), chiều cao mặt đáy bằng \(2\sqrt 3 cm\), cạnh đáy bằng 4cm. Tính thể tích hình chóp tam giác đều.
Đáp án : B Phương pháp giải :
B1: Tính chu vi đáy dựa vào công thức tính diện tích xung quanh hình lăng trụ đứng đáy là tam giác đều: \({S_{xq}} = C.h\) B2: Tính chiều cao hình lăng trụ đứng, từ đó suy ra chiều cao hình chóp tam giác đều. B3: Tính thể tích hình chóp đều theo công thức. Lời giải chi tiết :
Chu vi đáy ABC là: \(C = 4 + 4 + 4 = 12(cm)\) Chiều cao hình lăng trụ đứng là: \(h = {S_{xq}}:C = 36:12 = 3(cm)\) Từ hình vẽ ta thấy chiều cao hình chóp tam giác đều bằng chiều cao hình lăng trụ đứng đáy là tam giác đều nên chiều cao hình chóp bằng 3cm. Diện tích mặt đáy bằng: \({S_{ABC}} = \frac{1}{2}.4.2\sqrt 3 = 4\sqrt 3 (c{m^2})\) Áp dụng công thức thể tích khối chóp ta được: \(V = \frac{1}{3}.{S_{ABC}}.h = \frac{1}{3}.4\sqrt 3 .3 = 4\sqrt 3 c{m^3}\)
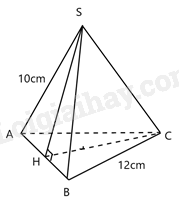
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về hình chóp đều, định lý Pythagore và công thức tính diện tích xung quanh của hình chóp đều. Lời giải chi tiết :
Vì S.ABC là hình chóp tam giác đều nên mặt bên SAB là tam giác cân tại S => SH là đường cao đồng thời là trung tuyến của tam giác SAB \( \Rightarrow AH = HB = \frac{{AB}}{2} = \frac{{12}}{2} = 6cm\) Xét tam giác vuông SHA có: \(SH = \sqrt {S{A^2} - H{A^2}} = \sqrt {{{10}^2} - {6^2}} = 8cm\) Nửa chu vi đáy của hình chóp: \(p = \frac{{12 + 12 + 12}}{2} = 18cm\) Vậy diện tích xung quanh của hình chóp S.ABC là \({S_{xq}} = p.d = 18.6 = 108c{m^2}\)
Câu 25 :
Cho hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau, chiều cao mặt đáy bằng \(3\sqrt 3 cm\). Tính chiều cao mặt bên hình chóp.
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về hình chóp đều, độ dài trung đoạn để tính. Lời giải chi tiết :
Hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau \( \Rightarrow SA = SB = SC = AB = AC = BC\). Gọi H là trọng tâm tam giác ABC đều , M là trung điểm BC. Theo định nghĩa trung đoạn, SM là trung đoạn của hình chóp. Đáy ABC là tam giác đều \( \Rightarrow \)AM vừa là trung tuyến vừa là đường cao\( \Rightarrow AM \bot BC \Rightarrow \widehat {AMB} = {90^0} \Rightarrow \Delta AMB\)vuông tại M. \(AM = 3\sqrt 3 cm\) Ta có: \(SA = SB = SC \Rightarrow \Delta SAB\) đều\( \Rightarrow \) SM vừa là trung tuyến vừa là đường cao.\( \Rightarrow SM \bot BC \Rightarrow \widehat {SMB} = {90^0} \Rightarrow \Delta SMB\) vuông tại M Xét tam giác vuông SMB và tam giác vuông AMB có: MB chung SB = AB \( \Rightarrow \Delta SMB = \Delta AMB\)(cạnh huyền – cạnh góc vuông) \( \Rightarrow SM = AM = 3\sqrt 3 (cm)\) Vậy độ dài trung đoạn SM bằng \(3\sqrt 3 cm\)
|