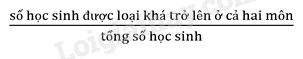Trắc nghiệm Bài 32: Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng Toán 8 Kết nối tri thứcĐề bài
Câu 1 :
Giả sử trong n lần thực nghiệm một hiện tượng ta thấy biến cố E xảy ra k lần, xác suất thực nghiệm của biến cố E tính bằng công thức nào?
Câu 2 :
Xác suất thực nghiệm càng gần xác suất khi?
Câu 3 :
Khi nói về xác suất thực nghiệm và xác suất. Chọn câu trả lời sai
Câu 4 :
Tỉ số
Câu 5 :
Nếu tung một đồng xu 13 lần liên tiếp; có 9 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu??
Câu 6 :
Minh tập bắn súng. Khi thực hiện bắn \(100\) lần thì có \(35\) lần trúng đích. Tính xác suất thực nghiệm của biến cố bắn trúng đích.
Câu 7 :
Trong trò chơi gieo xúc xắc, khi số lần gieo xúc xắc ngày càng lớn thì xác xuất thực nghiệm của biến cố: “Mặt xuất hiện của xúc xắc là mặt k chấm” ngày càng gần với số thực nào?
Câu 8 :
Trong trò chơi bánh xe quay số. Bánh xe số có \(20\) nấc điểm: \(5\) ; \(10\) ; \(15\) ; \(20\) ; …; \(100\) với các vạch chia đều nhau và giả sử rằng khả năng chuyển từ nấc điểm đã có tới các nấc điểm còn lại là như nhau. Trong mỗi lượt chơi có hai người tham gia, mỗi người được quay một lần và điểm của người chơi là điểm quay được. Người nào có số điểm cao hơn sẽ thắng cuộc, hòa nhau sẽ chơi lại lượt khác. Nam và Bình cùng tham gia một lượt chơi. Nam chơi trước và được \(85\) điểm. Hãy tính xác suất thực nghiệm của sự kiện Bình thắng cuộc ở lượt chơi này.
Câu 9 :
Cho dãy số liệu về số lượng đạt tuần học tốt của các lớp trong một năm học của một trường THCS như sau:
Hãy tính xác suất thực nghiệm của biến cố: “ Lớp được chọn là lớp đạt 8 tuần học tốt”
Câu 10 :
Tỉ lệ số học sinh đạt học sinh giỏi trong một lớp là \(15\% \) . Gặp ngẫu nhiên một bạn trong lớp. Tính xác suất thực nghiệm của biến cố : “Học sinh đó đạt học sinh giỏi”
Câu 11 :
Trong buổi thực hành môn Khoa học tự nhiên đo thể tích của vật thể không xác định được hình dạng, lớp 6A có 40 học sinh thực hiện phép đo thì có 35 học sinh thực hiện thành công. Em hãy tính xác suất thực nghiệm của biến cố: “Phép đo được thực hiện không thành công.”
Câu 12 :
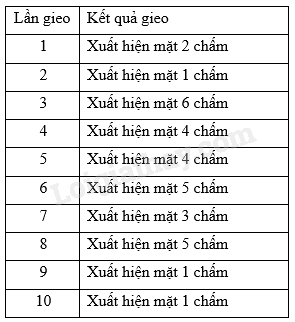
Gieo một xúc xắc \(10\) lần liên tiếp, bạn Cường có kết quả như sau:
Tính xác suất thực nghiệm xuất hiện mặt 1 chấm.
Câu 13 :
Một hộp chứa 3 viên bi xanh, 2 viên bi đỏ, 4 viên bi vàng. Lấy ngẫu nhiên 1 viên bi. Xác suất để viên bi lấy được là viên bi vàng là:
Câu 14 :
Bạn Hoàng Linh tung đồng xu 50 lần thấy có 30 lần xuất hiện mặt \(S\) còn bạn Tú Anh tung 100 lần và thấy có 55 lần xuất hiện mặt \(S\) . Bạn Hoàng Linh nói xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{30}}{{50}}\) ; còn bạn Tú Anh bảo rằng xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{55}}{{100}}\) . Vậy trong hai bạn thì bạn nào nói đúng ?
Câu 15 :
Trong trò chơi tung đồng xu, khi số lần tung đồng xu ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” ngày càng gần với số thực nào?
Câu 16 :
Kiểm tra ngẫu nhiên 100 chiếc máy tính của hãng X thì có 5 chiếc không đạt chất lượng. Hãy ước lượng xác suất của biến cố E: “Một máy tính của hãng X không đạt chất lượng?
Câu 17 :
Trong một hộp kín có ba quả bóng: một đỏ (Đ), một xanh (X), một vàng (V). Lấy ngẫu nhiên một bóng, xem màu, ghi kết quả rồi trả bóng vào hộp. Lặp lại các thao tác trên nhiều lần, kết quả ghi trong bảng sau:
Khả năng chọn được bóng của màu nào cao hơn?
Câu 18 :
Theo thống kê của một bệnh viện Sản, cứ 200 trẻ sơ sinh chào đời thì có 120 bé trai. Hãy ước lượng xem nếu có 1000 trẻ sơ sinh chào đời thì có bao nhiêu bé trai?
Câu 19 :
Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
Tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại khá trở lên ở cả 2 môn?
Câu 20 :
Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
Hãy tính xác suất thực nghiệm của biến cố:” Gieo được mặt có số chẵn chấm trong 50 lần gieo trên”.
Câu 21 :
Bạn An bỏ một số thẻ gỗ có đánh các số tự nhiên ( kích thước và khối lượng như nhau) vào trong một chiếc hộp. An lấy ra ngẫu nhiên một tấm thẻ, xem số rồi trả lại hộp. Lặp lại hành động đó 60 lần, An thấy có 24 lần lấy được thẻ ghi số chẵn. Biết trong hộp có 18 thẻ ghi số lẻ. Kết quả nào gần đúng với tổng số thẻ có trong hộp?
Lời giải và đáp án
Câu 1 :
Giả sử trong n lần thực nghiệm một hiện tượng ta thấy biến cố E xảy ra k lần, xác suất thực nghiệm của biến cố E tính bằng công thức nào?
Đáp án : B Phương pháp giải :
Giả sử trong n lần thực nghiệm một hiện tượng ta thấy biến cố E xảy ra k lần, xác suất thực nghiệm của biến cố E tính bằng công thức \(\frac{k}{n}\) . Lời giải chi tiết :
Giả sử trong n lần thực nghiệm một hiện tượng ta thấy biến cố E xảy ra k lần, xác suất thực nghiệm của biến cố E tính bằng công thức \(\frac{k}{n}\) nên chọn đáp án B.
Câu 2 :
Xác suất thực nghiệm càng gần xác suất khi?
Câu 3 :
Khi nói về xác suất thực nghiệm và xác suất. Chọn câu trả lời sai
Đáp án : C Phương pháp giải :
Sử dụng mối liên hệ giữa xác suất và xác suất thực nghiệm. Lời giải chi tiết :
Xác suất thực nghiệm được dùng để ước lượng xác suất của một biến cố khi các kết quả có thể của một hành động hay sự kiện không đồng khả năng nên chọn đáp án C
Câu 4 :
Tỉ số
Đáp án : A Phương pháp giải :
Lời giải chi tiết :
Xác suất thực nghiệm của biến cố E là tỉ số \(\frac{k}{n}\) trong đó k là số lần biến cố E xảy ra, n là số lần thực nghiệm hay theo dõi hiện tượng nên chọn đáp án A
Câu 5 :
Nếu tung một đồng xu 13 lần liên tiếp; có 9 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu??
Đáp án : A Phương pháp giải :
Dựa vào cách tính xác suất thực nghiệm. Lời giải chi tiết :
Nếu tung một đồng xu 13 lần liên tiếp; có 9 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng: \(\frac{9}{{13}}\)
Câu 6 :
Minh tập bắn súng. Khi thực hiện bắn \(100\) lần thì có \(35\) lần trúng đích. Tính xác suất thực nghiệm của biến cố bắn trúng đích.
Đáp án : A Phương pháp giải :
Dựa vào cách tính xác suất thực nghiệm. Lời giải chi tiết :
Theo công thức, xác suất thực nghiệm của sự kiện bắn trúng đích là \(\frac{{35}}{{100}} = \frac{7}{{20}}\)
Câu 7 :
Trong trò chơi gieo xúc xắc, khi số lần gieo xúc xắc ngày càng lớn thì xác xuất thực nghiệm của biến cố: “Mặt xuất hiện của xúc xắc là mặt k chấm” ngày càng gần với số thực nào?
Đáp án : B Phương pháp giải :
Dựa vào mối liên hệ giữa xác suất lí thuyết và xác suất thực nghiệm. Lời giải chi tiết :
Khi số lần gieo xúc xắc ngày càng lớn thì xác xuất thực nghiệm của biến cố: “Mặt xuất hiện của xúc xắc là mặt k chấm” ngày càng gần xác suất lí thuyết. Do xác xuất lí thuyết của biến cố : “Mặt xuất hiện của xúc xắc là mặt k chấm” là \(\frac{1}{6}\) nên xác xuất thực nghiệm của biến cố: “Mặt xuất hiện của xúc xắc là mặt k chấm” ngày càng gần với \(\frac{1}{6}\)
Câu 8 :
Trong trò chơi bánh xe quay số. Bánh xe số có \(20\) nấc điểm: \(5\) ; \(10\) ; \(15\) ; \(20\) ; …; \(100\) với các vạch chia đều nhau và giả sử rằng khả năng chuyển từ nấc điểm đã có tới các nấc điểm còn lại là như nhau. Trong mỗi lượt chơi có hai người tham gia, mỗi người được quay một lần và điểm của người chơi là điểm quay được. Người nào có số điểm cao hơn sẽ thắng cuộc, hòa nhau sẽ chơi lại lượt khác. Nam và Bình cùng tham gia một lượt chơi. Nam chơi trước và được \(85\) điểm. Hãy tính xác suất thực nghiệm của sự kiện Bình thắng cuộc ở lượt chơi này.
Đáp án : D Phương pháp giải :
Dựa vào cách tính xác suất thực nghiệm. Lời giải chi tiết :
Để Bình thắng ở lượt chơi này thì Bình phải quay vào các nấc điểm là \(90\) ; \(95\) ; \(100\) . Xác suất thực nghiệm của sự kiện Bình thắng ở lượt chơi này là: \(\frac{3}{{20}}\) .
Câu 9 :
Cho dãy số liệu về số lượng đạt tuần học tốt của các lớp trong một năm học của một trường THCS như sau:
Hãy tính xác suất thực nghiệm của biến cố: “ Lớp được chọn là lớp đạt 8 tuần học tốt”
Đáp án : D Phương pháp giải :
B1: Đếm tổng số lớp và đếm số lớp đạt 8 tuần học tốt. B2: Tính xác suất. Lời giải chi tiết :
Tổng số lớp là \(12\) lớp. Số lớp đạt 8 tuần học tốt là: 6 lớp Xác suất thực nghiệm của biến cố: “ Lớp được chọn là lớp đạt 8 tuần học tốt” là: \(\frac{6}{{12}} = 0,5\) .
Câu 10 :
Tỉ lệ số học sinh đạt học sinh giỏi trong một lớp là \(15\% \) . Gặp ngẫu nhiên một bạn trong lớp. Tính xác suất thực nghiệm của biến cố : “Học sinh đó đạt học sinh giỏi”
Đáp án : A Phương pháp giải :
Dựa vào lý thuyết xác suất thực nghiệm. Lời giải chi tiết :
Xác suất của biến cố : “Học sinh đó đạt học sinh giỏi” là \(\frac{{15}}{{100}} = 0,15\)
Câu 11 :
Trong buổi thực hành môn Khoa học tự nhiên đo thể tích của vật thể không xác định được hình dạng, lớp 6A có 40 học sinh thực hiện phép đo thì có 35 học sinh thực hiện thành công. Em hãy tính xác suất thực nghiệm của biến cố: “Phép đo được thực hiện không thành công.”
Đáp án : C Phương pháp giải :
Dựa vào cách tính xác suất thực nghiệm. B1: Tính số lần đo không thành công B2: Tính xác suất thực nghiệm. Lời giải chi tiết :
Số lần thực hiện phép đo là: \(40\) Sô lần đo không thành công là: \(40 - 35 = 5\) Xác suất thực nghiệm của biến cố: “Phép đo được thực hiện không thành công” là: \(\frac{5}{{40}} = \frac{1}{8}\)
Câu 12 :
Gieo một xúc xắc \(10\) lần liên tiếp, bạn Cường có kết quả như sau:
Tính xác suất thực nghiệm xuất hiện mặt 1 chấm.
Đáp án : C Phương pháp giải :
Dựa vào cách tính xác suất thực nghiệm. Lời giải chi tiết :
Số lần xuất hiện mặt 1 chấm: 3 lần Xác suất thực nghiệm xuất hiện mặt 1 chấm: \(\frac{3}{{10}}\)
Câu 13 :
Một hộp chứa 3 viên bi xanh, 2 viên bi đỏ, 4 viên bi vàng. Lấy ngẫu nhiên 1 viên bi. Xác suất để viên bi lấy được là viên bi vàng là:
Đáp án : B Phương pháp giải :
Dựa vào cách tính xác suất thực nghiệm. Lời giải chi tiết :
Tổng số viên bi trong hộp là : \(3 + 2 + 4 = 9\) (viên) Xác suất để viên bi lấy được là viên bi vàng là: \(\frac{4}{9}\)
Câu 14 :
Bạn Hoàng Linh tung đồng xu 50 lần thấy có 30 lần xuất hiện mặt \(S\) còn bạn Tú Anh tung 100 lần và thấy có 55 lần xuất hiện mặt \(S\) . Bạn Hoàng Linh nói xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{30}}{{50}}\) ; còn bạn Tú Anh bảo rằng xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{55}}{{100}}\) . Vậy trong hai bạn thì bạn nào nói đúng ?
Đáp án : C Phương pháp giải :
Dựa vào cách tính xác suất thực nghiệm. Lời giải chi tiết :
Bạn Hoàng Linh tung đồng xu 50 lần thấy có 30 lần xuất hiện mặt \(S\) nên xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{30}}{{50}}\) . Bạn Tú Anh tung 100 lần và thấy có 55 lần xuất hiện mặt \(S\) nên xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{55}}{{100}}\) .
Câu 15 :
Trong trò chơi tung đồng xu, khi số lần tung đồng xu ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” ngày càng gần với số thực nào?
Đáp án : A Phương pháp giải :
Dựa vào mối liên hệ giữa xác suất lí thuyết và xác suất thực nghiệm. Lời giải chi tiết :
Xác suất lí thuyết trong trò chơi đồng xu là \(\frac{1}{2} = 0,5\) . Khi số lần tung đồng xu ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” ngày càng gần xác suất lí thuyết nên xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” ngày càng gần với 0,5.
Câu 16 :
Kiểm tra ngẫu nhiên 100 chiếc máy tính của hãng X thì có 5 chiếc không đạt chất lượng. Hãy ước lượng xác suất của biến cố E: “Một máy tính của hãng X không đạt chất lượng?
Đáp án : B Phương pháp giải :
B1: Tính xác suất thực nghiệm của biến cố. B2: Ước lượng xác suất theo xác suất thực nghiệm. Lời giải chi tiết :
Trong 100 lần kiểm tra ta thấy biến cố “Một máy tính của hãng X không đạt chất lượng” xảy ra 5 lần Do đó xác suất thực nghiệm của biến cố là \(\frac{5}{{100}} = 0,05 = 5\% \) Vậy xác suất của biến cố “Một máy tính của hãng X không đạt chất lượng” được ước lượng là \(5\% \)
Câu 17 :
Trong một hộp kín có ba quả bóng: một đỏ (Đ), một xanh (X), một vàng (V). Lấy ngẫu nhiên một bóng, xem màu, ghi kết quả rồi trả bóng vào hộp. Lặp lại các thao tác trên nhiều lần, kết quả ghi trong bảng sau:
Khả năng chọn được bóng của màu nào cao hơn?
Đáp án : A Phương pháp giải :
B1: Tính tổng số lần lấy bóng. B2: Tính xác suất thực nghiệm của khả năng chọn được bóng màu xanh, đỏ, vàng. B3: So sánh và kết luận. Lời giải chi tiết :
Tổng số lần làm thực nghiệm là: \(15 + 15 + 20 = 50.\) Xác suất thực nghiệm của khả năng chọn được bóng màu đỏ là: \(\frac{{15}}{{50}} = 30\% \) Xác suất thực nghiệm của khả năng chọn được bóng màu vàng là: \(\frac{{20}}{{50}} = 40\% \) Xác suất thực nghiệm của khả năng chọn được bóng màu xanh là: \(\frac{{15}}{{50}} = 30\% \)
Câu 18 :
Theo thống kê của một bệnh viện Sản, cứ 200 trẻ sơ sinh chào đời thì có 120 bé trai. Hãy ước lượng xem nếu có 1000 trẻ sơ sinh chào đời thì có bao nhiêu bé trai?
Đáp án : B Phương pháp giải :
B1: Tính xác suất thực nghiệm của biến cố. B2: Ước lượng xác suất theo xác suất thực nghiệm. B3: Tính số bé trai Lời giải chi tiết :
Xác suất thực nghiệm của biến cố A: “ Bé chào đời là bé trai” là \(\frac{{120}}{{200}} = 0,6 = 60\% \) Do đó ta có các ước lượng sau: \(P(A) \approx 0,6\) Gọi k là số bé trai trong 1000 bé. Thay giá trị ước lượng ở trên ta được: \(\frac{k}{{1000}} \approx 0,6\) suy ra \(k \approx 600\) . Vậy trong 1000 bé ước lượng có khoảng 600 bé trai.
Câu 19 :
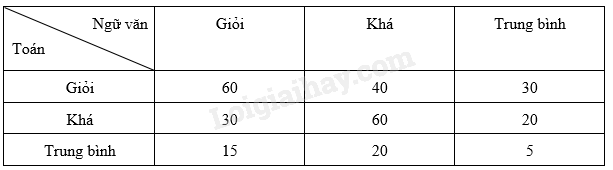
Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
Tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại khá trở lên ở cả 2 môn?
Đáp án : C Phương pháp giải :
B1: Tính tổng số học sinh B2: Tính số học sinh được loại khá trở lên ở cả hai môn.
Lời giải chi tiết :
Tổng số học sinh là tổng tất cả các số trên bảng: 280. Các học sinh được loại khá trở lên ở cả 2 môn: + Toán giỏi, Ngữ văn giỏi: 60 + Toán giỏi, Ngữ văn khá: 40 + Toán khá, Ngữ văn giỏi: 30 + Toán khá, Ngữ văn khá: 60 Số học sinh được loại khá trở lên ở cả 2 môn là: \(60 + 40 + 30 + 60 = 190\) Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại khá trở lên ở cả 2 môn là \(\frac{{190}}{{280}} = \frac{{19}}{{28}}\) Đáp án cần chọn là: C
Câu 20 :
Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
Hãy tính xác suất thực nghiệm của biến cố:” Gieo được mặt có số chẵn chấm trong 50 lần gieo trên”.
Đáp án : B Phương pháp giải :
B1: Tính số lần gieo được mặt chẵn. B2: Tính xác suất thực nghiệm của của biến cố:” Gieo được mặt có số chẵn chấm trong 50 lần gieo trên”. Lời giải chi tiết :
Tổng số lần gieo là 50. Các mặt có số lẻ chấm của con xúc xắc là mặt 2, 4 và 6. Số lần được mặt có số lẻ chấm là 8+12+6=26 lần. Xác suất thực nghiệm của của biến cố:” Gieo được mặt có số chẵn chấm trong 50 lần gieo trên” là: \(\frac{{26}}{{50}} = 0,52\) .
Câu 21 :
Bạn An bỏ một số thẻ gỗ có đánh các số tự nhiên ( kích thước và khối lượng như nhau) vào trong một chiếc hộp. An lấy ra ngẫu nhiên một tấm thẻ, xem số rồi trả lại hộp. Lặp lại hành động đó 60 lần, An thấy có 24 lần lấy được thẻ ghi số chẵn. Biết trong hộp có 18 thẻ ghi số lẻ. Kết quả nào gần đúng với tổng số thẻ có trong hộp?
Đáp án : A Phương pháp giải :
B1: Tính xác suất lí thuyết của biến cố: “Lấy được thẻ ghi số lẻ” B2: Tính xác suất thực nghiệm của biến cố: “Lấy được số thẻ ghi số lẻ trong 60 lần lấy thẻ. B3: Do số phép thử lớn nên xác suất thực nghiệm gần bằng với xác suất lí thuyết nên từ đó ta tìm được số thẻ trong hộp. Lời giải chi tiết :
Gọi n là tổng số thẻ có trong hộp. Xác suất lí thuyết của biến cố: “Lấy được thẻ ghi số lẻ” là \(\frac{{18}}{n}\) An thấy có 24 lần lấy được thẻ ghi số chẵn nên An có 60-24=36 lần lấy được thẻ ghi số lẻ. Xác suất thực nghiệm của biến cố: “Lấy được số thẻ ghi số lẻ trong 60 lần lấy thẻ” là \(\frac{{36}}{{60}} = \frac{3}{5}\) Do số phép thử lớn nên xác suất thực nghiệm gần bằng với xác suất lí thuyết nên ta có \(\frac{{18}}{n} \approx \frac{3}{5}\) nên \(n \approx 30\)
|