Trắc nghiệm Bài 16: Đường trung bình của tam giác Toán 8 Kết nối tri thứcĐề bài
Câu 1 :
Chọn câu đúng.
Câu 2 :
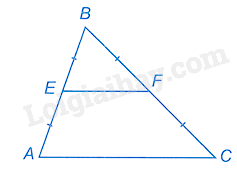
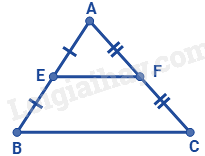
Cho tam giác ABC có E, F lần lượt là trung điểm của AB, BC. Phát biểu nào sau đây là đúng:
Câu 4 :
Cho các khẳng định dưới đây: 1) Trong một tam giác chỉ có một đường trung bình. 2) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. 3) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng cạnh ấy. Trong các khẳng định trên, số khẳng định đúng là
Câu 5 :
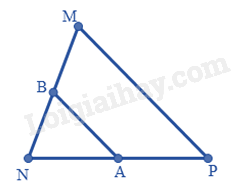
Cho tam giác MNP có A, B theo thứ tự là trung điểm của NP, MN. Biết AB = 3dm. Khi đó:
Câu 6 :
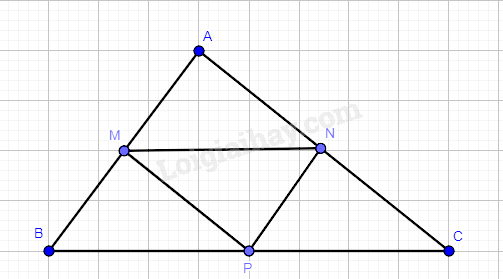
Cho tam giác ABC, gọi M, N và P lần lượt là trung điểm của AB, AC và BC. Hỏi có bao nhiêu hình thang trong hình vẽ ?
Câu 7 :
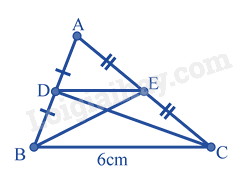
Cho tam giác ABC có BC = 6cm, các đường trung tuyến BE, CD. Khi đó độ dài cạnh DE là
Câu 8 :
Cho tam giác AMN như hình vẽ dưới đây. Biết AE = EM; AF = FN; EF = 9cm độ dài đoạn thẳng MN là
Câu 9 :
Hãy chọn câu đúng? Cho ΔABC, I, K lần lượt là trung điểm của AB và AC. Biết BC = 8 cm, AC = 7cm. Ta có:
Câu 11 :
Cho tam giác ABC. Trên cạnh AB, AC lần lượt lấy các điểm E, F sao cho AE = BE, AF = FC. Khi đó \(\frac{{BC}}{{EF}}\) bằng:
Câu 12 :
Cho tam giác ABC có chu vi bằng 32cm. Gọi E, F, P là trung điểm của các cạnh AB, BC, AC. Chu vi của tam giác PFE bằng:
Câu 14 :
Cho tam giác đều ABC cạnh 12cm. Gọi M, N lần lượt là trung điểm của AB và AC. Chu vi tứ giác MNBC là:
Câu 15 :
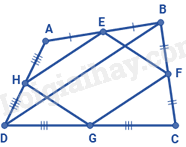
Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Biết BD = 18cm. Tổng độ dài hai đoạn thẳng HE và GF là:
Câu 16 :
Cho tam giác đều ABC có chu vi bằng 30cm. Độ dài đường trung bình ứng với cạnh AB là:
Câu 17 :
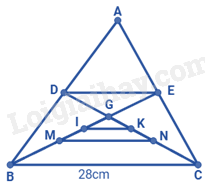
Cho hình dưới đây biết AD = DB, AE = EC, GM = MB; GN = NC, GI = IM; GK = KN; BC = 28cm. Khi đó tổng DE + IK bằng:
Câu 18 :
Cho tam giác ABC . Gọi D, E, F lần lượt là trung điểm của AB, AC, BC. Chu vi tam giác DEF là 21cm. Chu vi tam giác ABC là:
Câu 19 :
Cho tam giác ABC có AB = 24cm; AC = 36cm. Kẻ BD \(\left( {D \in AC} \right)\) vuông góc với tia phân giác của góc A tại H. Gọi M là trung điểm của BC. Độ dài đoạn thẳng HM là:
Câu 20 :
Cho tam giác ABC có AC < AB; \(\widehat A = {70^o}\) . Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi I, E, F lần lượt là trung điểm của CD, AD, CB. Số đo góc BEF bằng:
Lời giải và đáp án
Câu 1 :
Chọn câu đúng.
Đáp án : B Phương pháp giải :
Dựa vào định nghĩa đường trung bình của tam giác.
Lời giải chi tiết :
Đường trung bình của tam giác của tam giác là đoạn nối trung điểm hai cạnh của tam giác.
Câu 2 :
Cho tam giác ABC có E, F lần lượt là trung điểm của AB, BC. Phát biểu nào sau đây là đúng:
Đáp án : C Phương pháp giải :
Dựa vào tính chất của đường trung bình.
Lời giải chi tiết :
E, F lần lượt là trung điểm của AB, BC nên EF là đường trung bình của tam giác ABC. Suy ra EF có độ dài bằng một nửa của AC.
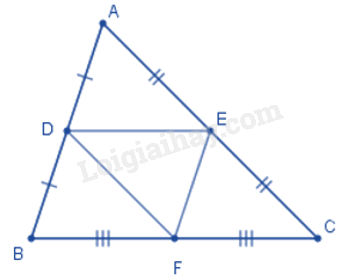
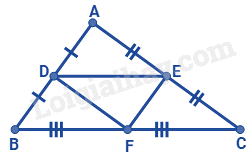
Đáp án : D Phương pháp giải :
Quan sát hình vẽ và dựa vào định nghĩa của đường trung bình của tam giác.
Lời giải chi tiết :
Xét tam giác ABC có D, E, F lần lượt là trung điểm các cạnh AB, AC, BC nên DE, DF, EF là ba đường trung bình của tam giác ABC.
Câu 4 :
Cho các khẳng định dưới đây: 1) Trong một tam giác chỉ có một đường trung bình. 2) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. 3) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng cạnh ấy. Trong các khẳng định trên, số khẳng định đúng là
Đáp án : B Phương pháp giải :
Dựa vào định nghĩa và tính chất của đường trung bình của tam giác.
Lời giải chi tiết :
Trong các khẳng định trên, chỉ có 1 khẳng định đúng là “Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác”.
Câu 5 :
Cho tam giác MNP có A, B theo thứ tự là trung điểm của NP, MN. Biết AB = 3dm. Khi đó:
Đáp án : A Phương pháp giải :
Sử dụng tính chất của đường trung bình của tam giác. Độ dài đường trung bình của tam giác bằng một nửa cạnh đáy.
Lời giải chi tiết :
Xét tam giác MNP có: A là trung điểm của NP B là trung điểm của MN Suy ra: \(AB = \frac{{MP}}{2} \Rightarrow MP = 2{\rm{A}}B = 2.3 = 6(dm)\)
Câu 6 :
Cho tam giác ABC, gọi M, N và P lần lượt là trung điểm của AB, AC và BC. Hỏi có bao nhiêu hình thang trong hình vẽ ?
Đáp án : B Phương pháp giải :
Vẽ hình và xác định các hình thang
Lời giải chi tiết :
Ta có: M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC. Suy ra: MN// BC Do đó, tứ giác MNCP, tứ giác MNPB và tứ giác MNCB là hình thang. * Tương tự, có MP là đường trung bình của tam giác nên MP// AC NP là đường trung bình của tam giác nên NP // AB. Các tứ giác: MPNA, MPCA và NPBA là hình thang. Vậy có tất cả 6 hình thang Chú ý
Hình bình hành cũng là hình thang.
Câu 7 :
Cho tam giác ABC có BC = 6cm, các đường trung tuyến BE, CD. Khi đó độ dài cạnh DE là
Đáp án : C Phương pháp giải :
Áp dụng tính chất của đường trung bình của tam giác.
Lời giải chi tiết :
Vì BE là trung tuyến của tam giác ABC suy ra E là trung điểm của AC Vì CD là trung tuyến của tam giác ABC suy ra D là trung điểm của AB Do đó DE là đường trung bình của tam giác ABC Xét tam giác ABC có DE là đường trung bình của tam giác ABC nên: \(DE = \frac{1}{2}BC = \frac{1}{2}.6 = 3(cm)\)
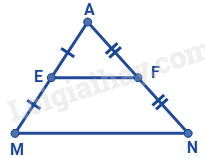
Câu 8 :
Cho tam giác AMN như hình vẽ dưới đây. Biết AE = EM; AF = FN; EF = 9cm độ dài đoạn thẳng MN là
Đáp án : C Phương pháp giải :
Chứng minh EF là đường trung bình của tam giác AMN và áp dụng tính chất của đường trung bình để tính độ dài của MN.
Lời giải chi tiết :
Vì AE = EM; AF = FN nên EF là đường trung bình của tam giác AMN Do đó: MN = 2. EF = 2.9 = 18cm
Câu 9 :
Hãy chọn câu đúng? Cho ΔABC, I, K lần lượt là trung điểm của AB và AC. Biết BC = 8 cm, AC = 7cm. Ta có:
Đáp án : A Phương pháp giải :
Dựa vào tính chất của đường trung bình của tam giác.
Lời giải chi tiết :
+ Vì I, K lần lượt là trung điểm của AB và AC nên IK là đường trung bình của tam giác ABC. => \(IK = \frac{1}{2}BC = \frac{1}{2}.8 = 4cm\) Vậy IK = 4cm
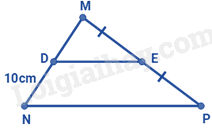
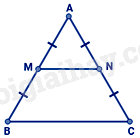
Đáp án : A Phương pháp giải :
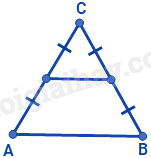
Chứng minh D là trung điểm của MN nên DM = DN
Lời giải chi tiết :
Vì ME = EP và DE // NP nên DM = DN. Lại có: DN = 10cm suy ra DM = 10cm.
Câu 11 :
Cho tam giác ABC. Trên cạnh AB, AC lần lượt lấy các điểm E, F sao cho AE = BE, AF = FC. Khi đó \(\frac{{BC}}{{EF}}\) bằng:
Đáp án : A Phương pháp giải :
Sử dụng tính chất đường trung bình của tam giác.
Lời giải chi tiết :
Vì AE = BE, AF = FC nên EF là đường trung bình của tam giác ABC. Do đó: BC = 2.EF. Vậy \(\frac{{BC}}{{EF}} = 2\).
Câu 12 :
Cho tam giác ABC có chu vi bằng 32cm. Gọi E, F, P là trung điểm của các cạnh AB, BC, AC. Chu vi của tam giác PFE bằng:
Đáp án : D Phương pháp giải :
Sử dụng tính chất đường trung bình của tam giác để ttính chu vi của tam giác PEF
Lời giải chi tiết :
Vì E. F, P là trung điểm của các cạnh AB. BC, AC của tam giác ABC nên EP, PF, FE là đường trung bình của tam giác ABC \( \Rightarrow EP = \frac{1}{2}BC;PF = \frac{1}{2}AB;F{\rm{E}} = \frac{1}{2}AC\) \( \Rightarrow EP + PF + F{\rm{E}} = \frac{1}{2}\left( {BC + AB + AC} \right) = \frac{1}{2}.32 = 16cm\)
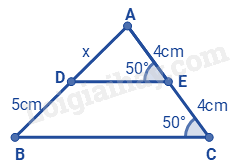
Đáp án : A Phương pháp giải :
Chứng minh D là trung điểm của AB
Lời giải chi tiết :
Ta có: AE = EC = 4cm (1) Đường thẳng AC cắt hai đoạn thẳng DE, BC tạo thành hai góc đồng vị: \(\widehat {A{\rm{ED}}} = \widehat {ECB} = {50^o}\) Suy ra: DE // BC (2) Từ (1) và (2) ta thấy DE đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai nên D đi qua trung điểm của cạnh AB Do đó: AD = BD = 5cm Hay x = 5cm
Câu 14 :
Cho tam giác đều ABC cạnh 12cm. Gọi M, N lần lượt là trung điểm của AB và AC. Chu vi tứ giác MNBC là:
Đáp án : B Phương pháp giải :
Tính độ dài các cạnh của tứ giác MNBC.
Lời giải chi tiết :
Vì M là trung điểm của AB, N là trung điểm của AC nên MN là đường trung bình của tam giác ABC: \( \Rightarrow MN = \frac{1}{2}BC = \frac{1}{{12}}.12 = 6cm\) Mặt khác: \(\begin{array}{l}MB = \frac{1}{2}AB = \frac{1}{2}.12 = 6cm\\NC = \frac{1}{2}.AC = \frac{1}{2}.12 = 6cm\end{array}\) Chu vi tứ giác MNBC là: BM + MN + NC + BC = 6 + 6 + 6 +12 = 30cm
Câu 15 :
Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Biết BD = 18cm. Tổng độ dài hai đoạn thẳng HE và GF là:
Đáp án : A Phương pháp giải :
Sử dụng tính chất đường trung bình của tam giác.
Lời giải chi tiết :
Xét tam giác ABD có H là trung điểm của AD, E là trung điểm của AB \( \Rightarrow HE\) là đường trung bình của tam giác ABD \( \Rightarrow HE = \frac{1}{2}B{\rm{D}} = \frac{1}{2}.18 = 9cm\) Xét tam giác CBD có F là trung điểm của BC, G là trung điểm của CD \( \Rightarrow GF\) là đường trung bình của tam giác CBD \( \Rightarrow GF = \frac{1}{2}B{\rm{D}} = \frac{1}{2}.18 = 9cm\) Tổng độ dài hai đoạn thẳng HE và GF là: 9 + 9 = 18cm
Câu 16 :
Cho tam giác đều ABC có chu vi bằng 30cm. Độ dài đường trung bình ứng với cạnh AB là:
Đáp án : A Phương pháp giải :
Tính độ dài cạnh của tam giác và sử dụng tính chất đường trung bình của tam giác
Lời giải chi tiết :
Vì tam giác ABC đều nên AC = AB = BC Mặt khác chu vi tam giác ABC bằng 30cm Suy ra độ dài cạnh AB là 30 : 3 = 10cm Độ dài đường trung bình ứng với cạnh AB là: \(\frac{1}{2}.10 = 5cm\) .
Câu 17 :
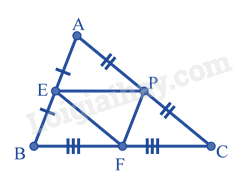
Cho hình dưới đây biết AD = DB, AE = EC, GM = MB; GN = NC, GI = IM; GK = KN; BC = 28cm. Khi đó tổng DE + IK bằng:
Đáp án : C Phương pháp giải :
Chứng minh DE, IK là đường trung bình của tam giác và sử dụng tính chất đường trung bình để tính độ dài của DE, IK.
Lời giải chi tiết :
Xét tam giác ABC có: AD = DB; AE = EC \( \Rightarrow DE\) là đường trung bình của tam giác ABC \( \Rightarrow DE = \frac{1}{2}BC = \frac{1}{2}.28 = 14cm\) Xét tam giác GBC có GM = MB; GN = NC \( \Rightarrow MN\) là đường trung bình của tam giác GBC \( \Rightarrow MN = \frac{{BC}}{2} = \frac{1}{2}.28 = 14cm\) Xét tam giác GMN có GM = MB; GN = NC \( \Rightarrow IK\) là đường trung bình của tam giác GMN \( \Rightarrow IK = \frac{{MN}}{2} = \frac{1}{2}.14 = 7cm\) Khi đó: DE + IK = 14 + 7 = 21cm
Câu 18 :
Cho tam giác ABC . Gọi D, E, F lần lượt là trung điểm của AB, AC, BC. Chu vi tam giác DEF là 21cm. Chu vi tam giác ABC là:
Đáp án : B Phương pháp giải :
Sử dụng tính chất đường trung bình của tam giác để tìm mối liên hệ giữa chu vi của tam giác DEF và tam giác ABC.
Lời giải chi tiết :
Vì D, E, F lần lượt là trung điểm của AB, AC, BC nên DE, EF, DF là các đường trung bình của tam giác ABC \( \Rightarrow DE = \frac{1}{2}BC;DF = \frac{1}{2}AC;{\rm{EF = }}\frac{1}{2}AB\) Do đó: \(DE + DF + {\rm{EF = }}\frac{1}{2}BC + \frac{1}{2}AC + \frac{1}{2}AB = \frac{1}{2}\left( {BC + AC + AB} \right)\) Khi đó chu vi tam giác DEF bằng \(\frac{1}{2}\) chu vi tam giác ABC Vậy chu vi tam giác ABC là: 2.21 = 42cm
Câu 19 :
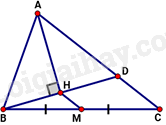
Cho tam giác ABC có AB = 24cm; AC = 36cm. Kẻ BD \(\left( {D \in AC} \right)\) vuông góc với tia phân giác của góc A tại H. Gọi M là trung điểm của BC. Độ dài đoạn thẳng HM là:
Đáp án : A Phương pháp giải :
Chứng minh HM là đường trung bình của tam giác BDC.
Lời giải chi tiết :
Vì AH là tia phân giác của goác BAC, AH vuông góc BD nên tam giác cân tại A. \( \Rightarrow AB = A{\rm{D}} = 24cm\) Do tam giác ABD cân tại A nên AH là đường phân giác đồng thời là đường trung tuyến của tam giác ABD Suy ra H là trung điểm của BD Ta có: DC = AC – AD = 36 – 24 = 12cm Xét tam giác BDC, ta có H là trung điểm của BD , M là trung điểm của BC nên HM là đường trung bình của tam giác BDC \( \Rightarrow HM = \frac{1}{2}DC = \frac{1}{2}.12 = 6cm\)
Câu 20 :
Cho tam giác ABC có AC < AB; \(\widehat A = {70^o}\) . Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi I, E, F lần lượt là trung điểm của CD, AD, CB. Số đo góc BEF bằng:
Đáp án : A Phương pháp giải :
Chứng minh EI, FI là các đường trung bình của tam giác => EI = FI => tam giác FDE cân tại I, ta tính được số đo góc BEF.
Lời giải chi tiết :
Xét tam giác ADC có E là trung điểm của AD, I là trung điểm của CD Suy ra: EI là đường trung bình của tam giác ADC Do đó \(EI//AC\) Nên \(\widehat {IE{\rm{D}}} = \widehat A = {70^o}\) (đồng vị) và \(EI = \frac{{AC}}{2}\) Tương tự: FI là đường trung bình của tam giác CBD Suy ra FI //BD; \(FI = \frac{{B{\rm{D}}}}{2}\) Do đó \(\widehat {{F_1}} = \widehat {{E_1}}\) (hai góc so le trong bằng nhau) Lại có: AC = BD (giả thiết), suy ra EI = FI Suy ra tam giác FIE cân tại I Do đó \(\widehat {{E_2}} = \widehat {{F_1}}\) Suy ra \(\widehat {{E_1}} = \widehat {{E_2}} = \frac{1}{2}\widehat {IE{\rm{D}}} = \frac{1}{2}.\widehat A = \frac{1}{2}.70 = {35^o}\)
|