Lý thuyết Một số hệ thức giữa cạnh, góc trong một tam giác vuông và ứng dụng Toán 9 Kết nối tri thức1. Hệ thức giữa cạnh huyền và cạnh góc vuông Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí 1. Hệ thức giữa cạnh huyền và cạnh góc vuông Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn
Ví dụ 1:
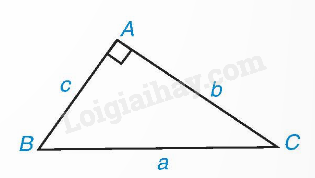
Trong tam giác ABC vuông tại A, ta có: \(\begin{array}{l}b = a.\sin B = a.\cos C;\\c = a.\sin C = a.\cos B.\end{array}\) 2. Hệ thức giữa hai cạnh góc vuông Công thức tính cạnh góc vuông theo cạnh góc vuông kia và tang, côtang của các góc nhọn
Ví dụ 2:
Trong tam giác ABC vuông tại A, ta có: \(\begin{array}{l}b = c.\tan B = c.\cot C;\\c = b.\tan C = b.\cot B.\end{array}\) 3. Giải tam giác vuông Bài toán Giải tam giác vuông Trong một tam giác vuông, nếu cho biết trước hai cạnh (hoặc một góc nhọn và một cạnh) thì ta sẽ tìm được tất cả các cạnh và các góc còn lại của tam giác vuông đó.    Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
