Bài 50 : Tính chất giao hoán của phép nhân

Bài 1

Viết số thích hợp vào chỗ chấm :

a) 125 × 6 = ...... × 125                                b) 364 × 9 = ..... × 364

c) 34 × (4 + 5) = 9 × .....                              d) (12 – 5) × 8 = ... × 7

Phương pháp giải:

Áp dụng tính chất giao hoán của phép nhân : 

Khi đổi chỗ các thừa số trong một tích thì tích không thay đổi.

\(a \times b=b \times a\)

Lời giải chi tiết:

a) 125 × 6 = 6 × 125                                    b) 364 × 9 = 9 × 364

c) 34 × (4 + 5) = 9 × 34                               d) (12 – 5) × 8 = 8 × 7

Bài 2

Tính theo mẫu :

Phương pháp giải:

Áp dụng tính chất giao hoán của phép nhân: 

Khi đổi chỗ các thừa số trong một tích thì tích không thay đổi. 

\(a \times b=b \times a\)

Lời giải chi tiết:

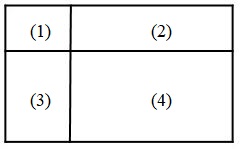
Bài 3

Khoanh vào chữ đặt trước câu trả lời đúng :

Trong hình bên có:

A. 5 hình chữ nhật                                      B. 6 hình chữ nhật

C. 8 hình chữ nhật                                      D. 9 hình chữ nhật

Phương pháp giải:

Quan sát hình vẽ rồi đếm các hình chữ nhật có trong hình. 

Lời giải chi tiết:

Trong hình đã cho có 9 hình chữ nhật, đó là: hình chữ nhật (1); hình chữ nhật (2) ; hình chữ nhật (3) ; hình chữ nhật (4); hình chữ nhật tạo bởi (1) + (2) ; hình chữ nhật tạo bởi (1) + (3) ; hình chữ nhật tạo bởi (2) + (4) ; hình chữ nhật tạo bởi (3) + (4) ; hình chữ nhật tạo bởi (1) + (2) + (3) + (4).

Chọn D. 9 hình chữ nhật.

Bài 4

Với 3 họ: Nguyễn, Trần, Lê và 4 tên: Hà, Nam, Bắc, Trung có thể ghép thành bao nhiêu họ tên khác nhau?

Phương pháp giải:

Lấy lần lượt 1 họ ghép với 1 tên khác nhau. Từ đó tìm được các tên họ khác nhau.

Lời giải chi tiết:

Ta lấy họ ghép lần lượt với các tên, từ đó ghép được thành 12 họ tên khác nhau, đó là :

+) Nguyễn Hà, Nguyễn Nam, Nguyễn Bắc, Nguyễn Trung.

+) Trần Hà, Trần Nam, Trần Bắc, Trần Trung.

+) Lê Hà, Lê Nam, Lê Bắc, Lê Trung.

HocTot.Nam.Name.Vn