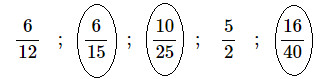Bài 101 : Rút gọn phân số

Bài 1

Rút gọn các phân số : 

\(\displaystyle\eqalign{
& {4 \over {12}} = ...\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad \quad\quad\quad{9 \over {18}} = ... \cr 
& {{24} \over {30}} = ...\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad \quad\quad\quad{{60} \over {36}} = ... \cr 
& {{25} \over {100}} = ...\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad \quad\quad\quad{{72} \over {54}} = ... \cr 
& {{60} \over {80}} = ...\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad \quad\quad\quad{{35} \over {210}} = ... \cr} \)

Phương pháp giải:

Cách rút gọn phân số :

- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

- Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).

Lời giải chi tiết:

Bài 2

Khoanh vào những phân số bằng \(\displaystyle {2 \over 5}\) :

\(\displaystyle{6 \over {12}}\,\,\;\;;\,\,\;\;{6 \over {15}}\,\,\;\;;\,\,\;\;{{10} \over {25}}\,\,\;\;;\,\,\;\;{5 \over 2}\,\,\;\;;\,\,\;\;{{16} \over {40}}\)

Phương pháp giải:

Rút gọn các phân số đã cho, phân số bằng phân số \(\displaystyle {2 \over 5}\) thì rút gọn được thành phân số tối giản là \(\displaystyle {2 \over 5}\).

Lời giải chi tiết:

Ta có :

\(\dfrac{6}{12} = \dfrac {6: 6}{ 12:6  } = \dfrac{1}{2}\)  ;                   \(\dfrac{6}{15} = \dfrac {6: 3}{ 15: 3 } = \dfrac{2}{5}\)

\(\dfrac{10}{25} = \dfrac {10:5 }{ 25: 5 } = \dfrac{2}{5}\)  ;                   \(\dfrac{16}{40} = \dfrac {16: 8}{40 :8  } = \dfrac{2}{5}\)

Phân số \(\dfrac{5}{2}\) có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\) nên là phân số tối giản.

Vậy ta có kết quả như sau :

Bài 3

 Khoanh vào chữ đặt trước câu trả lời đúng :

Trong các phân số \(\displaystyle{3 \over 9};  {3 \over {10}};{{11} \over {33}};{6 \over 9}\) phân số tối giản là:

A. \(\displaystyle{3 \over 9}\)                                            B. \(\displaystyle{3 \over {10}}\)

C. \(\displaystyle{{11} \over {33}}\)                                          D. \(\displaystyle{6 \over 9}\)

Phương pháp giải:

Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), hay phân số không thể rút gọn được nữa. 

Lời giải chi tiết:

Ta có : 

\(\dfrac{3}{9} = \dfrac {3: 3}{ 9: 3 } = \dfrac{1}{3}\)  ;              \(\dfrac{11}{33} = \dfrac {11: 11}{33 :11  } = \dfrac{1}{3}\)  ;

\(\dfrac{6}{9} = \dfrac {6: 3}{9 :3  } = \dfrac{2}{3}\) ;

Phân số \(\dfrac{3}{10}\) có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\) nên là phân số tối giản.

Chọn B.

HocTot.Nam.Name.Vn