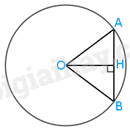
Giải bài tập 5.6 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức

Đề bài

Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó. Biết AB = 6 cm.

a) Tính khoảng cách từ O đến đường thẳng AB.

b) Tính$\tan \alpha$nếu góc ở tâm chắn cung AB bằng $2\alpha .$

Lời giải chi tiết

a) Kẻ $OH \bot AB$.

Ta có $\Delta AOB$ cân tại O (OA = OB), OH là đường cao nên OH cũng là đường trung tuyên của $\Delta OAB$

Suy ra H là trung điểm của AB nên $AH = HB = 3cm$

Xét $\Delta AHO$ vuông tại H, áp dụng định lý Pythagore, ta có:

$OH = \sqrt{OA^2-AH^2} = \sqrt{5^2-3^2}= 4 (cm)$ 

Vậy khoảng cách từ O đến AB là 4cm.

b) Ta có: $\widehat{AOB} = 2\alpha$.

OH là đường cao của tam giác AOB cân tại O nên OH cũng là đường phân giác của $\widehat{AOB}$

Suy ra $\widehat {AOH} = \widehat{BOH} = \alpha$

Tam giác AOH vuông tại H nên ta có:

$tan\alpha = \frac{AH}{OH} = \frac{3}{4}$