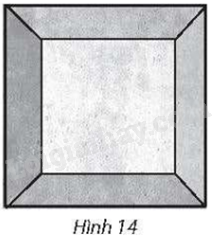
Giải bài 6 trang 62 sách bài tập toán 11 - Chân trời sáng tạo tập 2Người ta cần sơn tất cả các mặt của một khối bê tông hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 2m, đáy nhỏ có cạnh bằng 1m và cạnh bên bằng 2m (Hình 14). Tính tổng diện tích các bề mặt cần sơn. Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Người ta cần sơn tất cả các mặt của một khối bê tông hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 2m, đáy nhỏ có cạnh bằng 1m và cạnh bên bằng 2m (Hình 14). Tính tổng diện tích các bề mặt cần sơn.
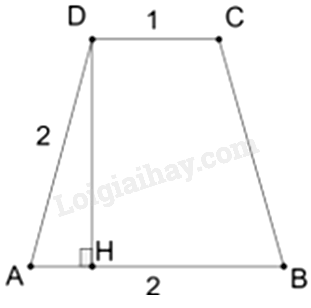
Phương pháp giải - Xem chi tiết Sử dụng kiến thức về diện tích toàn phần của hình chóp cụt tứ giác đều: S=SMB+SĐL+SĐN (MB: mặt bên, ĐL: đáy lớn, ĐN: đáy nhỏ) Lời giải chi tiết Diện tích đáy lớn là: SĐL=22=4(m2) Diện tích đáy nhỏ là: SĐN=12=1(m2) Giả sử các mặt bên được đặt tên và có dạng như hình vẽ dưới đây:
Tính được AH=12m. Áp dụng định lí Pythagore vào tam giác AHD vuông tại H có: DH=√AD2−AH2=√22−(12)2=√152(m) Tổng diện tích các mặt bên là: SMB=4SABCD=4.12(AB+CD).DH=3√15(m2) Tổng diện tích các mặt cần sơn là: S=SMB+SĐL+SĐN=3√15+4+1=3√15+5(m2)
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|