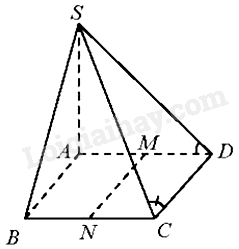
Giải bài 2 trang 51 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Đề bài

Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, $SA = a\sqrt 3 ,SA \bot AC,$ $SA \bot BC,$ $\widehat {BAD} = {120^0}$. Gọi M, N lần lượt là trung điểm của AD, BC. Tính góc giữa các cặp đường thẳng:

a) SD và BC.

b) MN và SC.

Lời giải chi tiết

a) Vì ABCD là hình thoi nên AD//BC. Do đó, $\left( {SD,BC} \right) = \left( {SD,AD} \right) = \widehat {SDA}$

Vì $SA \bot BC,$ AD//BC nên $SA \bot AD$. Do đó, tam giác SAD vuông tại A.

Do đó, $\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3  \Rightarrow \widehat {SDA} = {60^0}$

b) Vì M, N lần lượt là trung điểm của AD, BC nên MN//CD

Do đó, $\left( {MN,SC} \right) = \left( {CD,SC} \right) = \widehat {SCD}$

Áp dụng định lí Pythagore vào tam giác SAD vuông tại A có: $SD = \sqrt {S{A^2} + A{D^2}}  = \sqrt {3{a^2} + {a^2}}  = 2a$

Vì ABCD là hình thoi nên $AD = DC$. Do đó, tam giác ACD cân tại D

Vì ABCD là hình thoi nên AC là tia phân giác góc BAD. Do đó, $\widehat {DAC} = \frac{1}{2}\widehat {BAD} = {60^0}$

Suy ra, tam giác ACD đều nên $AC = a$

Áp dụng định lí Pythagore vào tam giác SAC vuông tại A có: $SC = \sqrt {S{A^2} + A{C^2}}  = \sqrt {3{a^2} + {a^2}}  = 2a$

Áp dụng định lý cosin vào tam giác SCD có:

$\cos \widehat {SCD} = \frac{{S{C^2} + C{D^2} - S{D^2}}}{{2.SC.CD}} = \frac{{{{\left( {2a} \right)}^2} + {a^2} - {{\left( {2a} \right)}^2}}}{{2.2a.a}} = \frac{1}{4} \Rightarrow \widehat {SCD} \approx 75,{5^0}$