Đề thi học kì 1 Toán 7 Kết nối tri thức - Đề số 17Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Chọn khẳng định đúng:
Câu 2 :
Viết gọn tích \({\left( {\frac{1}{3}} \right)^3}.{\left( {\frac{1}{3}} \right)^5}\) ta được:
Câu 3 :
Cho \(x = 6,67291\). Giá trị của \(x\) khi làm tròn đến chữ số thập phân thứ hai là:
Câu 4 :
Qua một điểm nằm ngoài một đường thẳng ta có thể kẻ được mấy đường thẳng song song với đường thẳng đó.
Câu 5 :
Nếu \(\sqrt x = 3\) thì \(x\) bằng
Câu 6 :
Câu nào dưới đây là đúng:
Câu 8 :
Cho \(\widehat {xOy} = 76^\circ \), tia Oz là tia phân giác của \(\widehat {xOy}\). Số đo của \(\widehat {yOz}\) là:
Câu 9 :
Cho \(\Delta ABC\) có \(\widehat A = 60^\circ ,\widehat B = 55^\circ \). Số đo của \(\widehat C\) là:
Câu 10 :
Chọn câu sai trong các câu sau:
Câu 11 :
Cho \(\Delta MNP = \Delta DHK\), khẳng định nào sau đây là đúng:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Chọn khẳng định đúng:
Đáp án : D Phương pháp giải :
Kiểm tra xem các số có thuộc tập hợp số đó hay không. \(\mathbb{N}\) là tập hợp số tự nhiên. \(\mathbb{Z}\) là tập hợp số nguyên. \(\mathbb{Q}\) là tập hợp số hữu tỉ. Lời giải chi tiết :
\( - 7\) không phải là số tự nhiên nên \( - 7 \in \mathbb{N}\) là sai. \(\frac{2}{3}\) không phải là số nguyên nên \(\frac{2}{3} \in \mathbb{Z}\) là sai. \(\frac{{ - 2}}{9}\) là số hữu tỉ nên \(\frac{{ - 2}}{9} \notin \mathbb{Q}\) là sai. \(\frac{1}{{10}}\) là số hữu tỉ nên \(\frac{1}{{10}} \in \mathbb{Q}\) là đúng. Đáp án D
Câu 2 :
Viết gọn tích \({\left( {\frac{1}{3}} \right)^3}.{\left( {\frac{1}{3}} \right)^5}\) ta được:
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về tích hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\). Lời giải chi tiết :
Ta có: \({\left( {\frac{1}{3}} \right)^3}.{\left( {\frac{1}{3}} \right)^5} = {\left( {\frac{1}{3}} \right)^{3 + 5}} = {\left( {\frac{1}{3}} \right)^8}\). Đáp án B
Câu 3 :
Cho \(x = 6,67291\). Giá trị của \(x\) khi làm tròn đến chữ số thập phân thứ hai là:
Đáp án : C Phương pháp giải :
Áp dụng quy tắc Làm tròn số thập phân dương: - Đối với chữ số hàng làm tròn: + Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5; + Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5. - Đối với chữ số sau hàng làm tròn: + Bỏ đi nếu ở phần thập phân; + Thay bằng các chữ số 0 nếu ở phần số nguyên. Lời giải chi tiết :
Số \(x = 6,67291\) khi làm tròn đến chữ số thập phân thứ hai là 6,67 (vì số 2 < 5). Đáp án C
Câu 4 :
Qua một điểm nằm ngoài một đường thẳng ta có thể kẻ được mấy đường thẳng song song với đường thẳng đó.
Đáp án : B Phương pháp giải :
Áp dụng tiên đề Euclid về đường thẳng song song. Lời giải chi tiết :
Qua một điểm nằm ngoài một đường thẳng, ta chỉ có thể kẻ được 1 đường thẳng song song với đường đó. Đáp án B
Câu 5 :
Nếu \(\sqrt x = 3\) thì \(x\) bằng
Đáp án : D Phương pháp giải :
Áp dụng kiến thức về căn bậc hai của một số: \(\sqrt x = a\) thì \(x = {a^2}\). Lời giải chi tiết :
Nếu \(\sqrt x = 3\) thì \(x = {3^2} = 9\). Đáp án D
Câu 6 :
Câu nào dưới đây là đúng:
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về giá trị tuyệt đối của một số: + Giá trị tuyệt đối của một số dương là chính nó + Giá trị tuyệt đối của một số âm là số đối của nó Lời giải chi tiết :
Nếu |x| = 3,9 thì x = 3,9 hoặc -3,9 nên đáp án A sai (chưa đủ kết quả của x). Nếu \(\left| { - x} \right| = 3,9\) thì \(x = - 3,9\) thì x = 3,9 hoặc -3,9 đều thỏa mãn nên B sai (chưa đủ kết quả của x). Nếu \(x = - 3,9\) thì \(\left| x \right| = \left| { - 3,9} \right| = 3,9\) nên C đúng. Nếu \( - x = 3,9\) thì \(x = - 3,9\) nên \(\left| { - x} \right| = \left| { - \left( { - 3,9} \right)} \right| = \left| {3,9} \right| = 3,9\) nên D sai Đáp án C
Đáp án : C Phương pháp giải :
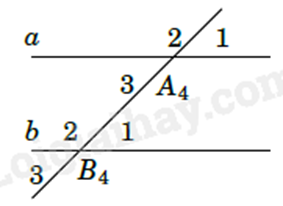
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau. Lời giải chi tiết :
Quan sát hình vẽ, ta thấy hai góc \(\widehat {{A_1}}\) và \(\widehat {{B_1}}\) ở vị trí đồng vị nên nếu \(\widehat {{A_1}} = \widehat {{B_1}}\) thì đường thẳng a song song với b. Đáp án C
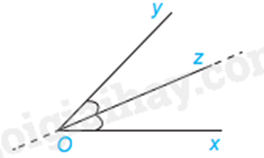
Câu 8 :
Cho \(\widehat {xOy} = 76^\circ \), tia Oz là tia phân giác của \(\widehat {xOy}\). Số đo của \(\widehat {yOz}\) là:
Đáp án : C Phương pháp giải :
Sử dụng tính chất của tia phân giác: tia phân giác chia một góc thành hai góc bằng nhau và bằng một nửa góc đó. Lời giải chi tiết :
Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {yOz} = \frac{1}{2}\widehat {xOy} = \frac{1}{2}.76^\circ = 38^\circ \). Đáp án C
Câu 9 :
Cho \(\Delta ABC\) có \(\widehat A = 60^\circ ,\widehat B = 55^\circ \). Số đo của \(\widehat C\) là:
Đáp án : B Phương pháp giải :
Áp dụng định lí tổng ba góc của một tam giác bằng \(180^\circ \). Lời giải chi tiết :
Tam giác ABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) suy ra \(\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 60^\circ - 55^\circ = 65^\circ \). Đáp án B
Câu 10 :
Chọn câu sai trong các câu sau:
Đáp án : C Phương pháp giải :
So sánh số hữu tỉ với nhau. Lời giải chi tiết :
\(0,45 < 0,5\) suy ra C sai. Đáp án C
Câu 11 :
Cho \(\Delta MNP = \Delta DHK\), khẳng định nào sau đây là đúng:
Đáp án : C Phương pháp giải :
Hai tam giác bằng nhau thì các cạnh tương ứng và các góc tương ứng bằng nhau. Lời giải chi tiết :
\(\Delta MNP = \Delta DHK\) thì \(\widehat M = \widehat D;\widehat N = \widehat H;\widehat P = \widehat K\) và \(MN = DH;MP = DK;NP = HK\). Vậy ta chọn đáp án C Đáp án C
Đáp án : D Phương pháp giải :
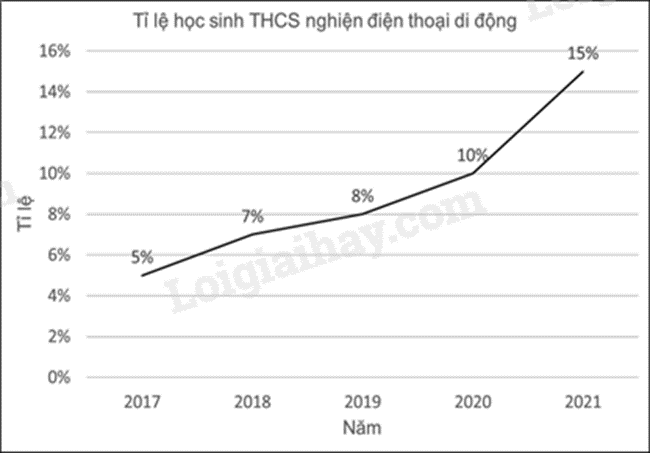
Quan sát xem điểm biểu diễn năm nào lớn nhất thì năm đó có tỉ lệ học sinh THCS nghiện điện thoại cao nhất. Lời giải chi tiết :
Ta thấy năm 2021 có tỉ lệ lớn nhất (15%) nên tỉ lệ học sinh THCS nghiện điện thoại năm 2021 cao nhất Đáp án D
II. Tự luận
Phương pháp giải :
a) Sử dụng tính chất kết hợp để đưa các số thành các nhóm. b) Thực hiện phép tính với số hữu tỉ và căn bậc hai của một số hữu tỉ. c) Sử dụng tính chất phân phối của phép nhân với phép trừ. Lời giải chi tiết :
a) \(\frac{{11}}{{24}} + \frac{{ - 5}}{{41}} + \frac{{13}}{{24}} + \frac{{ - 36}}{{41}} + \frac{1}{2}\) \(\begin{array}{l} = \left( {\frac{{11}}{{24}} + \frac{{13}}{{24}}} \right) + \left( {\frac{{ - 5}}{{41}} + \frac{{ - 36}}{{41}}} \right) + \frac{1}{2}\\ = \frac{{24}}{{24}} + \frac{{ - 41}}{{41}} + \frac{1}{2}\\ = 1 - 1 + \frac{1}{2} = \frac{1}{2}\end{array}\) b) \(\frac{2}{5} + \frac{3}{5}.\frac{7}{6} - \sqrt {\frac{{16}}{{25}}} \) \(\begin{array}{l} = \frac{2}{5} + \frac{3}{5}.\frac{7}{6} - \frac{4}{5}\\ = \frac{2}{5} + \frac{7}{{10}} - \frac{4}{5}\\ = \frac{{2.2 + 7 - 4.2}}{{10}}\\ = \frac{3}{{10}}\end{array}\) c) \(\frac{4}{5}.1\frac{2}{9} - \frac{4}{5}.\frac{2}{9} + \frac{3}{5}\) \(\begin{array}{l} = \frac{4}{5}.\left( {1\frac{2}{9} - \frac{2}{9}} \right) + \frac{3}{5}\\ = \frac{4}{5}.1 + \frac{3}{5}\\ = \frac{4}{5} + \frac{3}{5} = \frac{7}{5}\end{array}\) Phương pháp giải :
Áp dụng quy tắc chuyển vế đổi dấu. c) Đưa về dạng \(\left| A \right| = B\), chia hai trường hợp: A = B hoặc A = -B. Lời giải chi tiết :
a) \(x - \frac{1}{4} = \frac{2}{3}\) \(\begin{array}{l}x = \frac{2}{3} + \frac{1}{4}\\x = \frac{{11}}{{12}}\end{array}\) Vậy \(x = \frac{{11}}{{12}}\) b) \(\frac{1}{4} + \frac{3}{4}x = \frac{{ - 13}}{8}\) \(\begin{array}{l}\frac{3}{4}x = \frac{{ - 13}}{8} - \frac{1}{4}\\\frac{3}{4}x = \frac{{ - 15}}{8}\\x = \frac{{ - 15}}{8}:\frac{3}{4}\\x = \frac{{ - 5}}{2}\end{array}\) Vậy \(x = \frac{{ - 5}}{2}\) c) \(\left| {\frac{3}{4}x - \frac{1}{2}} \right| + {\left( {\frac{{ - 1}}{2}} \right)^2} = \sqrt {\frac{4}{9}} \) \(\begin{array}{l}\left| {\frac{3}{4}x - \frac{1}{2}} \right| + \frac{1}{4} = \frac{2}{3}\\\left| {\frac{3}{4}x - \frac{1}{2}} \right| = \frac{2}{3} - \frac{1}{4}\\\left| {\frac{3}{4}x - \frac{1}{2}} \right| = \frac{5}{{12}}\\\frac{3}{4}x - \frac{1}{2} = \pm \frac{5}{{12}}\end{array}\) TH1: \(\frac{3}{4}x - \frac{1}{2} = \frac{5}{{12}}\) \(\begin{array}{l}\frac{3}{4}x = \frac{5}{{12}} + \frac{1}{2}\\\frac{3}{4}x = \frac{{11}}{{12}}\\x = \frac{{11}}{{12}}:\frac{3}{4}\\x = \frac{{11}}{9}\end{array}\) TH2: \(\frac{3}{4}x - \frac{1}{2} = - \frac{5}{{12}}\) \(\begin{array}{l}\frac{3}{4}x = - \frac{5}{{12}} + \frac{1}{2}\\\frac{3}{4}x = \frac{1}{{12}}\\x = \frac{1}{{12}}:\frac{3}{4}\\x = \frac{1}{9}\end{array}\) Vậy \(x \in \left\{ {\frac{{11}}{9};\frac{1}{9}} \right\}\) Phương pháp giải :
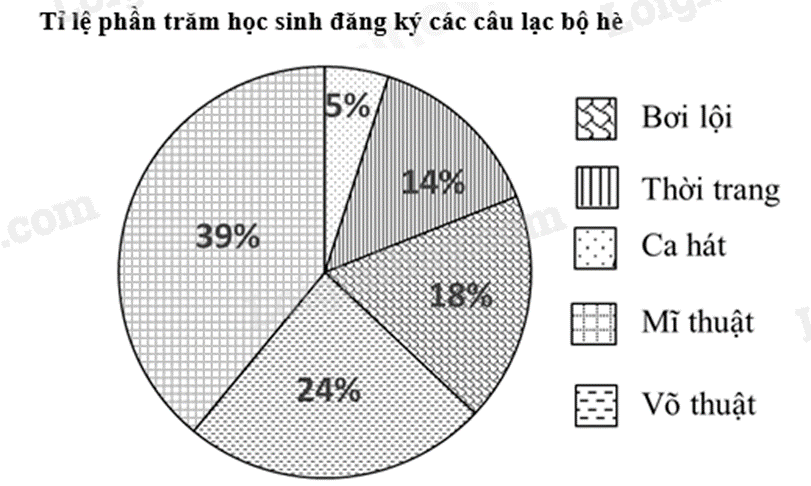
a) Quan sát biểu đồ, câu lạc bộ được yêu thích nhất có tỉ lệ phần trăm học sinh đăng ký nhiều nhất. b) Từ số liệu trong biểu đồ để lập bảng thống kê. c) Tính giá trị phần trăm m% của một số a cho trước theo công thức: \(m\% .a\). Lời giải chi tiết :
a) Câu lạc bộ được học sinh yêu thích nhất khi đăng ký là Mĩ thuật (39%). b) Bảng thống kê:
c) Số học sinh đăng ký câu lạc bộ bơi lội là: \(18\% .500 = 90\) (học sinh) Phương pháp giải :
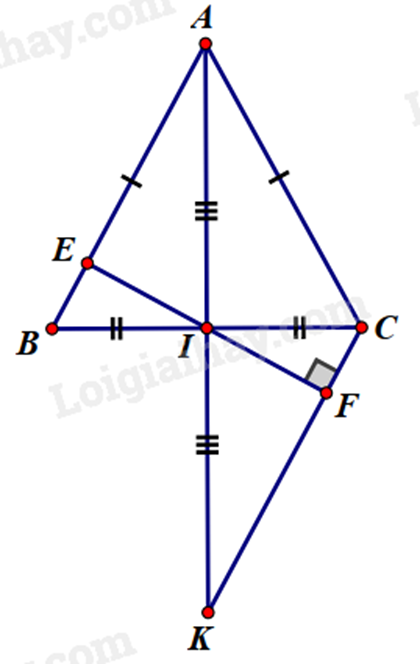
a) Chứng minh \(\Delta ABI = \Delta ACI\) theo trường hợp cạnh – cạnh – cạnh. Suy ra \(\widehat {AIB} = \widehat {AIC}\). Mà hai góc này kề bù nên suy ra \(\widehat {AIB} = 90^\circ \) hay \(AI \bot BC\). b) Chứng minh \(\Delta ABI = \Delta KCI\) suy ra AB = KC. c) Chứng minh \(\Delta BIE = \Delta CIF\) suy ra \(\widehat {BIE} = \widehat {CIF}\). Sử dụng tính chất hai góc kề bù suy ra \(\widehat {EIF} = 180^\circ \) nên E, I, F thẳng hàng. Lời giải chi tiết :
a) Xét \(\Delta ABI\) và \(\Delta ACI\) có: \(AB = AC\) (gt) \(BI = CI\) (I là trung điểm của BC) \(AI\) chung Suy ra \(\Delta ABI = \Delta ACI\) (c.c.c) Suy ra \(\widehat {AIB} = \widehat {AIC}\). Mà hai góc này kề bù nên \(\widehat {AIB} + \widehat {AIC} = 180^\circ \), suy ra \(\widehat {AIB} = \widehat {AIC} = \frac{{180^\circ }}{2} = 90^\circ \) hay \(AI \bot BC\). b) Xét \(\Delta ABI\) và \(\Delta KCI\) có: \(AI = KI\) (gt) \(\widehat {AIB} = \widehat {KIC}\left( { = 90^\circ } \right)\) \(BI = CI\) Suy ra \(\Delta ABI = \Delta KCI\) (c.g.c) suy ra AB = KC. c) Vì \(\Delta ABI = \Delta KCI\) nên \(\widehat {ABI} = \widehat {KCI}\) Xét \(\Delta BIE\) và \(\Delta CIF\) ta có: \(\widehat {BEI} = \widehat {CFI}\left( { = 90^\circ } \right)\) \(\widehat {EBI} = \widehat {FCI}\) \(BI = CI\) Suy ra \(\Delta BIE = \Delta CIF\) (cạnh huyền – góc nhọn) Do đó \(\widehat {BIE} = \widehat {CIF}\). Mà \(\widehat {BIE}\) và \(\widehat {EIC}\) là hai góc kề bù nên \(\widehat {BIE} + \widehat {EIC} = 180^\circ \) nên \(\widehat {EIC} + \widehat {CIF} = 180^\circ \) hay \(\widehat {EIF} = 180^\circ \) nên E, I, F thẳng hàng. Phương pháp giải :
Biến đổi các phân số thành \(\frac{{{n^2} - 1}}{{{n^2}}}\) để rút gọn S. Chứng minh \(n - 2 < S < n - 1\) nên S không là số nguyên. Lời giải chi tiết :
Ta có: \(\begin{array}{l}S = \frac{3}{4} + \frac{8}{9} + \frac{{15}}{{16}} + ... + \frac{{{n^2} - 1}}{{{n^2}}}\\ = \frac{{{2^2} - 1}}{{{2^2}}} + \frac{{{3^2} - 1}}{{{3^2}}} + \frac{{{4^2} - 1}}{{{4^2}}} + ... + \frac{{{n^2} - 1}}{{{n^2}}}\\ = 1 - \frac{1}{{{2^2}}} + 1 - \frac{1}{{{3^2}}} + 1 - \frac{1}{{{4^2}}} + ...1 + \frac{1}{{{n^2}}}\\ = \left( {1 + 1 + ... + 1} \right) - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}} \right)\\ = \left( {n - 1} \right) - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}} \right)\end{array}\) +) Vì \(\left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}} \right) > 0\) nên \(S < n - 1\) (1) +) \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}} < \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{\left( {n - 1} \right).n}} = 1 - \frac{1}{n} < 1\) Suy ra \( - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}} \right) > - 1\) Suy ra \(\left( {n - 1} \right) - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}} \right) > \left( {n - 1} \right) - 1 = n - 2\) Do đó \(S > n - 2\) (2) Từ (1) và (2) suy ra \(n - 2 < S < n - 1\) Vì giữa n – 2 và n – 1 không có số nguyên nào nên S không là số nguyên.
|