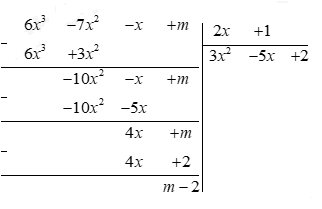Đề thi học kì 2 Toán 7 - Đề số 7Tải về I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài I. TRẮC NGHIỆM (2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Có bao nhiêu đơn thức trong các biểu thức \(2x \left( {y + 3} \right); 3{x^2}y ; \dfrac{1}{{2x}}; x + 5y ; x\left( { - y} \right)?\) A. 1. B. 2. C. 3. D. 4. Câu 2: Độ dài hai cạnh của một tam giác là 3cm và 10cm. Trong các số đo sau đây, số đo nào là độ dài cạnh thức ba của tam giác đó? A. 13 cm. B. 7 cm. C. 8 cm. D. 14 cm. Câu 3: Một điểm M thuộc đường trung trực d của một đoạn thẳng AB thì A. M là trung điểm của AB. B. MA = MB. C. MA > MB. D. Cả A, B, C đều đúng. Câu 4: Cho \(\Delta ABC\) có đường trung tuyến BD và \(G\) là trọng tâm. Khi đó A. \(BG = \dfrac{3}{2}BD\) B. \(GB = \dfrac{1}{2}GD\) C. \(GD = \dfrac{1}{3}BD\) D. \(BD = \dfrac{2}{3}BG\) Câu 5: Cho tam giác ABC các đường phân giác AM của góc \(A\) và \(B{\rm{N}}\) của góc \(B\) cắt nhau tại \(I\). Khi đó, điểm \(I\) : A. Là trực tâm của tam giác B. Cách hai đỉnh A và B một khoảng lần lượt bằng \(\dfrac{2}{3}AM\) và \(\dfrac{2}{3}B{\rm{N}}\) C. Cách đều ba cạnh của tam giác D. Cách đều ba đỉnh của tam giác Câu 6: Giá trị của biểu thức \(A = 2x\left( {3x - 1} \right) - 6x\left( {x + 1} \right) - \left( {3 - 8x} \right)\) là: A. \( - 16x - 3\) B. \( - 3\) C. \( - 16x\) D. Đáp án khác Câu 7: Xác suất của biến cố trong trò chơi gieo xúc xắc bằng A. Tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc B. Tỉ số của số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc và số các kết quả thuận lợi cho biến cố C. Hiệu của số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc và số các kết quả thuận lợi cho biến cố D. Tích của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc Câu 8: Tìm dư của phép chia \(A = 3{x^3} - 2{x^2} + 4x + 1\) cho \(B = {x^2} + 3x + 2\). A. 32x + 23. B. 31x + 23. C. 32x + 31. D. 30x + 23. II. TỰ LUẬN Câu 1 Có \(3\) gói tiền: gói thứ nhất gồm toàn tờ bạc \(20000\) đồng, gói thứ hai gồm toàn tờ bạc \(50000\) đồng, gói thứ ba gồm toàn tờ bạc \(100000\) đồng. Biết số tiền ở ba gói bằng nhau và gói thứ nhất hơn gói thứ ba \(68\) tờ giấy bạc. Hỏi mỗi loại có bao nhiêu tờ giấy bạc và tổng số tiền ở cả ba gói là bao nhiêu ? Câu 2: Cho hai đa thức \(f\left( x \right) = {x^4} + 7{x^3} + 11{x^2} - 2x - 1 - \left( {{x^3} - 4{x^2}} \right)\left( {x - 2} \right)\); \(g\left( x \right) = {x^3} + 3{x^2} + 3x - 2\) a) Thu gọn và xác định hệ số cao nhất của \(f\left( x \right)\). b) Xác định giá trị của \(g\left( 1 \right);g\left( 2 \right)\). c) Tính \(h\left( x \right) = g\left( x \right) - f\left( x \right)\) và tìm nghiệm của \(h\left( x \right)\). Câu 3: Cho đa thức \(A\left( x \right) = 6{x^3} - 7{x^2} - x + m\) và \(B\left( x \right) = 2x + 1\) a) Thực hiện phép chia \(A\left( x \right)\) cho \(B\left( x \right)\). b) Tìm giá trị của \(m\) để phép chia trên có dư là \(4\). Câu 4: Cho \(\Delta ABC\) có \(\angle B = {90^\circ }\), AD là tia phân giác của \(\angle A\) (\(D \in BC\)). Trên tia AC lấy điểm E sao cho \(AB = AE\); kẻ \(BH \bot AC\)\(\left( {H \in AC} \right)\). a) Chứng minh \(\Delta ABD = \Delta AED; DE \bot AE\). b) Chứng minh AD là đường trung trực của đoạn thẳng BE. c) So sánh EH và EC. Câu 5: Tìm các hệ số a, b, c thoả mãn \(\left( {ax + b} \right)\left( {{x^2} - 2cx + abc} \right) = {x^3} - 7{x^2} + 3x + 3\) với mọi x. Lời giải I. Trắc nghiệm
Câu 1 Phương pháp: Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến. Cách giải: Vậy có hai đơn thức là \( 3{x^2}y ; x\left( { - y} \right)\). Chọn B. Câu 2 Phương pháp: Sử dụng hệ quả của bất đẳng thức trong tam giác: + Tồn tại một tam giác có độ dài ba cạnh là a,b,c nếu \(\left| {b - c} \right| < a < b + c\). + Trong trường hợp xác định được \(a\) là số lớn nhất trong ba số a,b,c thì điều kiện tồn tại tam giác là \(a < b + c\) Cách giải: Gọi độ dài cạnh thứ ba của tam giác là \(c\left( {c > 0} \right)\) Ta có: \(\left| {3 - 10} \right| < c < 3 + 10\) (hệ quả của bất đẳng thức trong tam giác) \( \Rightarrow 7 < c < 13\) Do đó, độ dài cạnh thứ ba của tam giác là 8cm. Chọn C. Câu 3 Phương pháp: Sử dụng tính chất đường trung trực của đoạn thẳng: Điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó. Cách giải: Một điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó nên MA = MB. Do đó B đúng, C sai, D sai. M chưa chắc là trung điểm của AB, nên A sai. Chọn B. Câu 4 Phương pháp: Sử dụng tính chất ba đường trung tuyến trong tam giác. Cách giải:
\(\Delta ABC\) có \(G\) là trọng tâm \( \Rightarrow GD = \dfrac{1}{3}BD\) (tính chất ba đường trung tuyến trong tam giác) Chọn C. Câu 5 Phương pháp: Tính chất ba đường phân giác trong tam giác: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ban cạnh của tam giác đó. Cách giải:
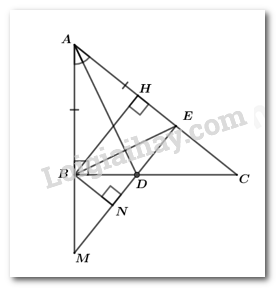
Cho tam giác ABC các đường phân giác AM của góc \(A\) và \(B{\rm{N}}\) của góc \(B\) cắt nhau tại \(I\) Khi đó, điểm \(I\)cách đều ba cạnh của tam giác. Chọn C. Câu 6 Cách giải: \(A = 2x\left( {3x - 1} \right) - 6x\left( {x + 1} \right) - \left( {3 - 8x} \right) = 6{x^2} - 2x - 6{x^2} - 6x - 3 + 8x = - 3\). Chọn B. Câu 7 Phương pháp: Xác suất của biến cố trong trò chơi gieo xúc xắc bằng tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc. Cách giải: Xác suất của biến cố trong trò chơi gieo xúc xắc bằng tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc. Chọn A. Câu 8 Phương pháp: Đặt tính chia đa thức cho đa thức rồi tìm dư. Cách giải: Chọn B. II. PHẦN TỰ LUẬN (8,0 điểm) Câu 1 Phương pháp: - Gọi số tờ tiền của mỗi loại là \(a,b,c.\) - Dựa vào đề bài, viết các tỉ lệ thức liên quan, áp dụng tính chất dãy tỉ số bằng nhau để tìm lời giải cho bài toán. Cách giải: Gọi số tờ tiền của mỗi loại giấy bạc \(20000\) đồng, \(50000\) đồng và \(100000\) đồng lần lượt là \(a,b,c\left( {a,b,c \in {\mathbb{N}^*},a > 68} \right)\) Số tiền ở ba gói lần lượt là : \(20\,000a\) đồng; \(50000b\) đồng và \(100000c\) đồng. Do số tiền ở ba gói là bằng nhau nên ta có : \(20000a = 50000b = 100000c\) Chia cả ba vế cho \(100000\) ta được tỉ lệ thức: \(\dfrac{a}{5} = \dfrac{b}{2} = \dfrac{c}{1}\) Mà gói thứ nhất hơn gói thứ ba \(68\) tờ giấy bạc hay \(a - c = 68\) Áp dụng tính chất dãy tỉ số bằng nhau ta có : \(\dfrac{a}{5} = \dfrac{b}{2} = \dfrac{c}{1} = \dfrac{{a - c}}{{5 - 1}} = \dfrac{{68}}{4} = 17\) \( \Rightarrow \left\{ \begin{array}{l}\dfrac{a}{5} = 17 \Rightarrow a = 17.5 = 85\\\dfrac{b}{2} = 17 \Rightarrow b = 17.2 = 34\\\dfrac{c}{1} = 17 \Rightarrow c = 17.1 = 17\end{array} \right.\) Vậy có \(85\) tờ \(20000\) đồng, \(34\) tờ \(50000\) đồng và \(17\) tờ \(100000\) đồng. Khi đó mỗi gói có số tiền là : \(20000 \times 85 = 1700000\) (đồng) Tổng số tiền ở cả ba gói là : \(1700000 \times 3 = 5100000\) (đồng) Câu 2 Phương pháp: Thực hiện phép tính bằng cách phối hợp các cách nhân, chia, cộng, trừ đa thức và đơn thức rồi rút gọn. Cách giải: a)\(f\left( x \right) = {x^4} + 7{x^3} + 11{x^2} - 2x - 1 - \left( {{x^3} - 4{x^2}} \right)\left( {x - 2} \right)\) \(\begin{array}{*{20}{l}}{f\left( x \right) = {x^4} - 5{x^3} + 11{x^2} - 2x - {x^4} + 2{x^3} + 4{x^3} - 8{x^2}}\\{f\left( x \right) = \left( {{x^4} - {x^4}} \right) + \left( {2{x^3} + 4{x^3} - 5{x^3}} \right) + \left( {11{x^2} - 8{x^2}} \right) - 2x}\\{f\left( x \right) = {x^3} + 3{x^2} - 2x}\end{array}\) Hệ số cao nhất là 1. b) \(g\left( 1 \right) = {1^3} + {3.1^2} + 3.1 - 2 = 5\) \(g\left( 2 \right) = {2^3} + {3.2^2} + 3.2 - 2 = 24\) c) \(h\left( x \right) = g\left( x \right) - f\left( x \right) = {x^3} + 3{x^2} + 3x - 2 - \left( {{x^3} + 3{x^2} - 2x} \right)\) \(\begin{array}{*{20}{l}}{h\left( x \right) = {x^3} + 3{x^2} + 3x - 2 - {x^3} - 3{x^2} + 2x}\\{h\left( x \right) = \left( {{x^3} - {x^3}} \right) + \left( {3{x^2} - 3{x^2}} \right) + \left( {3x + 2x} \right) - 2}\\{h\left( x \right) = 5x - 2}\end{array}\) \(h\left( x \right) = 5x - 2 = 0 \Rightarrow x = \dfrac{2}{5}\). Câu 3 Phương pháp: Với hai đa thức một biến \(A\) và \(B\)(\(B\) khác đa thức \(0\)) tuỳ ý. Tồn tại hai đa thức duy nhất \(Q\) và \(R\) sao cho: \(A = B.Q + R\) trong đó bậc của \(R\) thấp hơn bậc của \(B\) A: đa thức bị chia B: Đa thức chia Q: Đa thức thương \(R\): Đa thức dư Cách giải: a) Ta thực hiện phép chia \(A\left( x \right):B\left( x \right)\) Vậy \(\left( {6{x^3} - 7{x^2} - x + m} \right):\left( {2x + 1} \right)\) được thương là \(3{x^2} - 5x + 2\) dư \(m - 2\) b) Để \(A\left( x \right):B\left( x \right)\) dư \(4\) thì \(m - 2 = 4 \Leftrightarrow m = 6\) Vậy khi \(m = 6\) thì \(A\left( x \right):B\left( x \right)\) dư \(4\). Câu 4 Phương pháp: + Sử dụng các cách chứng minh hai tam giác bằng nhau. + Tính chất các đường cao, đường phân giác, đường trung trực trong tam giác cân. Cách giải: a) Xét \(\Delta ABD\)và\(\Delta AED\)có: + AD chung \( + AB = AE(gt)\) + \(\angle BAD = \angle EAD\)(vì AD là tia phân giác của \(\widehat {BAC}\)) \( \Rightarrow \Delta ABD = \)\(\Delta AED\) (c.g.c) (đpcm) \( \Rightarrow \widehat {AED} = \widehat {ABD} = {90^\circ }\) (hai góc tương ứng) \( \Rightarrow DE \bot AE\)(đpcm) b) Vì AB = AE (gt) \( \Rightarrow \Delta ABE\) cân tại A. Lại có ADlà tia phân giác của \(\widehat {BAE}\) nên AD cũng là đường trung trực của BE. c) + Do \(AM = AN\)\( \Rightarrow \Delta AMN\)cân tại \(A\) Vì ADlà tia phân giác của góc \(A\)nên suy ra ADđồng thời là đường cao trong \(\Delta AMN\)ứng với cạnh MN. \( \Rightarrow AD \bot MN\) (đpcm). (4) + \(\Delta ABC\)có ADlà tia phân giác của góc \(A\)nên suy ra AD đồng thời là đường cao ứng với cạnh BC. \( \Rightarrow AD \bot BC\) (5) Từ (4), (5) suy ra \(MN//BC\) (đpcm) d) Vì \(\Delta ABD = \Delta AED\) (câu a) \( \Rightarrow BD = DE\). Gọi \(M = AB \cap DE\), kẻ \(BN \bot ME\), \(\left( {N \in ME} \right)\). Vì \(\left. {\begin{array}{*{20}{l}}{BH \bot AC(gt)}\\{DE \bot AC (cmt)}\end{array}} \right\} \Rightarrow BH//DE\) (từ vuông góc đến song song) \( \Rightarrow \widehat {HBE} = \widehat {BEN}\) (2 góc so le trong) Xét \(\Delta BHE\) và \(\Delta ENB\) có: + \(\widehat {BHE} = \widehat {ENB} = {90^\circ }\) + BE là cạnh chung + \(\widehat {HBE} = \widehat {BEN}\) (cmt) \( \Rightarrow \Delta BHE = \Delta ENB\)(g.c.g) \( \Rightarrow EH = NB\) (*) Xét \(\Delta BDM\) và \(\Delta EDC\) có: + \(\widehat {DBM} = \widehat {DEC} = {90^\circ }\) + \(BD = DE\) (cmt) + \(\widehat {BDM} = \widehat {EDC}\) (đối đỉnh) \( \Rightarrow \Delta BDM = \Delta EDC\)(g.c.g) \( \Rightarrow BM = EC\) (**) Xét tam giác vuông BNM có BN là cạnh góc vuông, BM là cạnh huyền \( \Rightarrow BM > BN\) (***) Từ (*), (**), (***) \( \Rightarrow EC > EH\). Câu 5 Phương pháp: Nhân đa thức ở vế trái ra rồi đồng nhất thức với vế phải. Cách giải: \(\begin{array}{*{20}{l}}{\left( {ax + b} \right)\left( {{x^2} - 2cx + abc} \right)}\\{ = a{x^3} - 2ac{x^2} + {a^2}bcx + b{x^2} - 2bcx + a{b^2}c}\\{ = a{x^3} + \left( {b - 2ac} \right){x^2} + \left( {{a^2}bc - 2bc} \right)x + a{b^2}c}\end{array}\) Suy ra \(\left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b - 2ac = {\rm{ \;}} - 4}\\{{a^2}bc - 2bc = 3}\\{a{b^2}c = 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b - 2c = {\rm{ \;}} - 7}\\{bc - 2bc = 3}\\{{b^2}c = 3}\end{array}} \right.} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b - 2c = {\rm{ \;}} - 7}\\{bc = {\rm{ \;}} - 3}\\{b = {\rm{ \;}} - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = {\rm{ \;}} - 1}\\{c = 3}\end{array}} \right.\) Vậy \(\left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = {\rm{ \;}} - 1}\\{c = 3}\end{array}} \right.\).
|