Đề thi học kì 2 Toán 7 - Đề số 3 - Kết nối tri thứcTải về I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
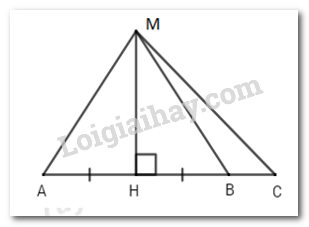
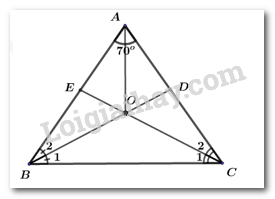
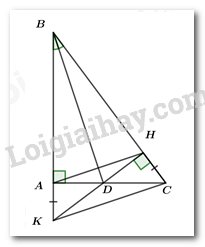
Đề bài I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1. Trong chuyến du lịch tại Đà Nẵng, Nhi quen được một người bạn mới cũng là người Việt Nam nhưng lại quên quê hương của người bạn ấy. Hỏi có tất cả bao nhiêu tỉnh thành có thể là quê hương của người bạn mới đó? A. 43; B. 53; C. 63; D. 73. Câu 2: Cho biết \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch, biết khi \(x = 5\) thì \(y = 10\). Vậy khi \(x = 2\) thì \(y\) bằng bao nhiêu? A. \(2\) B. \(25\) C. \(10\) D.\(20\) Câu 3. Cho \(\Delta ABC,{\mkern 1mu} \hat A = {70^\circ }\), hai đường phân giác BD và CE cắt nhau tại \(O\), thế thì: A. \(\widehat {BOC} = {120^\circ }\). B. \(\widehat {BAO} = \dfrac{1}{2}\widehat {BAC}\). C. \(\widehat {BOC} = {160^\circ }\). D. \(\widehat {BAO} < {30^\circ }\). Câu 4: Cho hình lăng trụ đứng có đáy là hình thang với đáy bé bằng \(5\,cm,\) đáy lớn bằng \(7\,cm\) và hai cạnh bên lần lượt bằng \(3\,cm;\,4cm.\) Biết chiều cao của hình lăng trụ đứng đó là \(8\,cm.\) Diện tích xung quanh của hình lăng trụ đứng đó là: A. \(152\,c{m^2}\) B. \(76\,c{m^2}\) C. \(159\,c{m^2}\) D. \(159\,cm\) Câu 5: Tính chất nào sau đây không phải của tam giác\(ABC\)cân tại \(C\): A. Trung tuyến \(AM\)và \(BN\)của tam giác \(ABC\) bằng nhau. B. \(\angle A < {90^o}\). C. \(AC > AB\). D. \(\angle A = \angle B\) Câu 6. \(5m\) dây đồng nặng \(43g\). Hỏi \(10km\) dây đồng như thế nặng bao nhiêu kilôgam? A. \(86kg\) B. \(84kg\) C. \(76kg\) D. \(72kg\) Câu 7. Cho hình vẽ sau: Em hãy chọn đáp án sai trong các đáp án sau: A. \(MA > MH\) B. \(HB < HC\) C. \(MA = MB\) D. \(MC < MA.\) Câu 8. Cho hai đa thức \(f(x) = - {x^5} + 2{x^4} - {x^2} - 1;g(x) = - 6 + 2x - 3{x^3} - {x^4} + 3{x^5}\). Giá trị của \(\)\(h(x) = f(x) - g(x)\) tại x = -1 là: A. –8 B. –12 C. 10 D. 18 II. PHẦN TỰ LUẬN (8,0 điểm) Bài 1. (1 điểm) Tìm \(x\) biết: a) \( - 0,1:x = - 0,2:0,06\) b) \(\dfrac{{2 - x}}{4} = \dfrac{{3x - 1}}{3}\) Bài 2. (1,5 điểm) Ba đơn vị kinh doanh A, B và C góp vốn theo tỉ lệ \(2\,\,:3\,\,:\,\,7\) sau một năm thu được tổng cộng \(960\) triệu đồng tiền lãi. Hỏi mỗi đơn vị được chia bao nhiêu tiền lãi biết tiền lãi được chia tỉ lệ thuận với số vốn đã góp. Bài 3. (2 điểm) Cho các đa thức: \(F\left( x \right) = 5{x^2} - 1 + 3x + {x^2} - 5{x^3}\) và \(G\left( x \right) = 2 - 3{x^3} + 6{x^2} + 5x - 2{x^3} - x.\) a) Thu gọn và sắp xếp hai đa thức \(F\left( x \right)\) và \(G\left( x \right)\) theo lũy thừa giảm dần của biến. b) Tính \(M\left( x \right) = F\left( x \right) - G\left( x \right)\); Tìm nghiệm của đa thức \(M\left( x \right)\) c) Tìm đa thức \(N\left( x \right)\) biết \(N\left( x \right) + F\left( x \right) = - G\left( x \right)\) Bài 4. (3 điểm) Cho tam giác\(ABC\)vuông tại\(A\)và có đường phân giác \(BD\). Kẻ đường thẳng \(DH\)vuông có với \(BC\)tại điểm \(H\). Trên tia đối của tia \(AB\)lấy điểm \(K\)sao cho \(AK = CH\). a) Chứng minh rằng \(\Delta ABD = \Delta HBD\). b) Chứng minh rằng: Đường thẳng \(BD\)là đường trung trực của đoạn thẳng \(AH\)và \(AD < DC\). c) Chứng minh rằng: Ba điểm \(H,D,K\)thẳng hàng và đường thẳng \(BD\)vuông góc với đường thẳng \(KC\). d) Chứng minh rằng: \(2\left( {AD + AK} \right) > CK\) Cho \(\Delta ABC\)cân tại \(A\), tia phân giác của \(\angle BAC\) cắt cạnh \(BC\)tại \(D\). Kẻ \(DH\)vuông góc với \(AB\)tại \(H\), kẻ \(DK\)vuông Bài 5. (0,5 điểm) Cho đa thức \(f\left( x \right)\) thỏa mãn \(f\left( x \right) + x.f\left( { - x} \right) = x + 1\) với mọi giá trị của \(x\). Tính \(f\left( 1 \right)\). Câu 2 I. Trắc nghiệm
Câu 1: Phương pháp: Vì Việt Nam có tất cả 63 tỉnh nên quê hương của bạn mới đó có thể là 1 trong 63 tỉnh. Cách giải: Vì Việt Nam có tất cả 63 tỉnh nên quê hương của bạn mới đó có thể là 1 trong 63 tỉnh. Chọn C. Câu 2: Phương pháp: Vận dụng kiến thức về hai đại lượng tỉ lệ nghịch với nhau. Cách giải: \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch với nhau \( \Rightarrow y = \dfrac{a}{x}\left( {a \ne 0} \right)\) Thay \(x = 5;y = 10\) vào ta được: \(10 = \dfrac{a}{5} \Rightarrow a = 10.5 = 50\) Vậy hệ số tỉ lệ của \(y\) so với \(x\) là \(50\). Ta có: \(y = \dfrac{{50}}{x}\), khi \(x = 2\) thì \(y = \dfrac{{50}}{2} = 25\). Chọn B. Câu 3: Phương pháp: Sử dụng tính chất tia phân giác của góc và định lí tổng 3 góc trong một tam giác. Cách giải:
Ta có: \(\widehat {BOC} = {180^\circ }{\rm{ \;}} - \widehat {{B_1}} - \widehat {{C_1}}\). Vì BD và CE lần lượt là các tia phân giác của góc B và C nên ta có: \(\widehat {{B_1}} = \dfrac{{\hat B}}{2};{\mkern 1mu} \widehat {{C_1}} = \dfrac{{\hat C}}{2}\). Trong tam giác ABC ta có: \(\hat B + \hat C = {180^\circ }{\rm{ \;}} - \hat A = {180^\circ }{\rm{ \;}} - {70^\circ }{\rm{ \;}} = {110^\circ }\). \( \Rightarrow \widehat {BOC} = {180^\circ }{\rm{ \;}} - \widehat {{B_1}} - \widehat {{C_1}} = {180^\circ }{\rm{ \;}} - \dfrac{{\hat B + \hat C}}{2} = {180^\circ }{\rm{ \;}} - {55^\circ }{\rm{ \;}} = {125^\circ }\) Chọn B. Câu 4: Phương pháp: Áp dụng công thức tính diện tích xung quanh của hình lăng trụ đứng tứ giác là \({S_{xq}} = C.h\) (trong đó \(C\) là chu vi đáy và \(h\) là chiều cao của hình lăng trụ) Bước 1: Tính chu vi đáy của hình lăng trụ đứng Bước 2: Tính diện tích xung quanh hình lăng trụ đứng Cách giải: Chu vi đáy của hình lăng trụ đứng đã cho là: \(C = 5 + 7 + 3 + 4 = 19\left( {cm} \right)\) Diện tích xung quanh của hình lăng trụ đứng tứ giác đó là: \({S_{xq}} = C.h = 19.8 = 152\,c{m^2}\) Chọn A. Câu 5
Phương pháp: + Tam giác cân có hai góc ở đáy bằng nhau. + Tam giác cân có hai đường trung tuyến ứng với hai cạnh bên bằng nhau. + Tổng ba góc trong một tam giác bằng \({180^o}\) Cách giải: + Theo tính chất của tam giác cân thì A, D đúng. + Ta có \(\angle A = \angle B = \dfrac{{{{180}^o} - \angle C}}{2} < {90^o}\) . Vậy B đúng. + Tam giác ABC cân tại C thì \(AC > AB\)hoặc \(AC \le AB\). Vậy đáp án C sai. Chọn C. Câu 6. Phương pháp: Gọi số gam trong \(10\,000m\) dây đồng là \(x\left( g \right)\) Vì khối lượng của dây đồng tỉ lệ thuận với chiều dài của dây đồng nên lập được dãy tỉ số bằng nhau, từ đó tìm được \(x\). Cách giải: Đổi \(10km = 10\,000m\) Gọi số gam trong \(10\,000m\) dây đồng là \(x\left( g \right)\) Vì khối lượng của dây đồng tỉ lệ thuận với chiều dài của dây đồng nên ta có: \(\dfrac{{43}}{5} = \dfrac{x}{{10\,000}}\) Suy ra \(x = \dfrac{{43}}{5}.10\,000 = 86\,000\left( g \right) = 86\left( {kg} \right)\) Vậy \(10km\) dây đồng nặng \(86kg\) Chọn A. Câu 7. Phương pháp: Áp dụng các định lý sau: - Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu. - Quan hệ giữa góc và cạnh trong tam giác. Cách giải: Vì MH là đường vuông góc và MA là đường xiên nên \(MA > MH\)(quan hệ đường vuông góc và đường xiên). Đáp án A đúng nên loại A. Vì \(\angle MBC\) là góc ngoài của \(\Delta MHB\left( {gt} \right) \Rightarrow \angle MBC > \angle MHB = {90^0}\) Xét \(\Delta MBC\) có: \(\angle MBC\) là góc tù nên suy ra \(MC > MB\) (quan hệ giữa góc và cạnh trong tam giác) Mà HB và HC lần lượt là hình chiếu của MB và MC trên AC. \( \Rightarrow HB < HC\) (quan hệ giữa đường xiên và hình chiếu). Đáp án B đúng nên loại đáp án B. Vì \(AH = HB\left( {gt} \right)\) mà AH và HB lần lượt là hai hình chiếu của AM và BM. \( \Rightarrow MA = MB\)(quan hệ giữa đường xiên và hình chiếu). Đáp án C đúng nên loại đáp án C. Ta có: \(\left\{ {\begin{array}{*{20}{l}}{MB = MA\left( {cmt} \right)}\\{MC > MB\left( {cmt} \right)}\end{array}} \right. \Rightarrow MC > MA\) . Đáp án D sai nên chọn đáp án D. Chọn D. Câu 8. Phương pháp: - Để trừ hai đa thức, ta nhóm các hạng tử cùng bậc với nhau và rút gọn. - Thay \(x = - 1\) vào đa thức h(x) vừa tìm được để tìm giá trị của h(x). Cách giải: \(\begin{array}{l}h(x) = f(x) - g(x) = \left( { - {x^5} + 2{x^4} - {x^2} - 1} \right) - \left( { - 6 + 2x - 3{x^3} - {x^4} + 3{x^5}} \right)\,\,\,\\\;\;\;\;\;\;\; = - {x^5} + 2{x^4} - {x^2} - 1 + 6 - 2x + 3{x^3} + {x^4} - 3{x^5}\\\;\;\;\;\;\;\; = \left( { - {x^5} - 3{x^5}} \right) + \left( {2{x^4} + {x^4}} \right) + 3{x^3} - {x^2} - 2x + 5\\\;\;\;\;\;\;\; = - 4{x^5} + 3{x^4} + 3{x^3} - {x^2} - 2x + 5.\end{array}\) Thay \(x = - 1\) vào đa thức h(x) ta có: \(h( - 1) = - 4.{( - 1)^5} + 3.{( - 1)^4} + 3.{( - 1)^3} - {( - 1)^2} - 2.( - 1) + 5 = - 4.( - 1) + 3.1 + 3.( - 1) - 1 + 2 + 5 = 10\) Vậy giá trị của h(x) là 10 tại \(x = - 1\). Chọn C II. PHẦN TỰ LUẬN (8,0 điểm) Bài 1. Phương pháp Vận dụng tính chất của tỉ lệ thức: Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\) từ đó tìm \(x\) Cách giải: a) \( - 0,1:x = - 0,2:0,06\) \(\begin{array}{l}\dfrac{{ - 0,1}}{x} = \dfrac{{ - 0,2}}{{0,06}}\\\dfrac{{ - 0,1}}{x} = \dfrac{{ - 1}}{5}:\dfrac{3}{{50}}\\\dfrac{{ - 0,1}}{x} = \dfrac{{ - 1}}{5}.\dfrac{{50}}{3}\\\dfrac{{ - 0,1}}{x} = \dfrac{{ - 10}}{3}\end{array}\) Áp dụng tính chất tỉ lệ thức ta có: \(\begin{array}{l} - 0,1.3 = - 10x\\ - 0,3 = - 10x\\x = - 0,3:\left( { - 10} \right)\\x = \dfrac{{ - 3}}{{10}}.\left( {\dfrac{1}{{ - 10}}} \right)\\x = \dfrac{3}{{100}}\end{array}\) Vậy \(x = \dfrac{3}{{100}}\) b) \(\dfrac{{2 - x}}{4} = \dfrac{{3x - 1}}{3}\) \(\begin{array}{l}3\left( {2 - x} \right) = 4\left( {3x - 1} \right)\\6 - 3x = 12x - 4\\ - 3x - 12x = - 4 - 6\\ - 15x = - 10\\x = \dfrac{2}{3}\end{array}\) Vậy \(x = \dfrac{2}{3}\) Câu 2 Phương pháp: Gọi số tiền lãi của ba đơn vị kinh doanh A, B và C lần lượt là \(x,y,z\) (triệu đồng) (điều kiện: \(x,y,z \in \mathbb{N}\)) Áp dụng tính chất của dãy tỉ số bằng nhau để giải toán. Cách giải: Gọi số tiền lãi của ba đơn vị kinh doanh A, B và C lần lượt là \(x,y,z\) (triệu đồng) (điều kiện: \(x,y,z > 0\)) Theo bài ra, ta có: \(\left\{ \begin{array}{l}\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{7}\\x + y + z = 960\end{array} \right.\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{7} = \dfrac{{x + y + z}}{{2 + 3 + 7}} = \dfrac{{960}}{{12}} = 80\) Khi đó, \(\dfrac{x}{2} = 80 \Rightarrow x = 160\) (tmđk) \(\dfrac{y}{3} = 80 \Rightarrow y = 240\) (tmđk) \(\dfrac{z}{7} = 80 \Rightarrow y = 560\) (tmđk) Vậy số tiền lãi của ba đơn vị kinh doanh là: Đơn vị A: 160 triệu đồng, đơn vị B: 240 triệu đồng, đơn vị C: 560 triệu đồng. Bài 3. Phương pháp a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến của hai đa thức \(F\left( x \right)\) và \(G\left( x \right)\). Khi thu gọn các đơn thức đồng dạng ta cộng hệ số với nhau và giữ nguyên phần biến, sau đó sắp xếp theo lũy thừa giảm dần của biến số. b) Tính \(M\left( x \right) = F\left( x \right) - G\left( x \right)\). Ta thực hiện trừ hai đa thức. Sau đó tìm nghiệm của đa thức \(M\left( x \right)\), ta cho \(M\left( x \right) = 0\) để tìm nghiệm. c) Biến đổi \(N\left( x \right) + F\left( x \right) = - G\left( x \right) \Rightarrow N\left( x \right) = - F\left( x \right) - G\left( x \right)\), rồi thực hiện tính. Chú ý: Trước dấu trừ các hạng tử đổi dấu. Cách giải: a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến. Thu gọn \(F\left( x \right):\) \(\begin{array}{l}F\left( x \right) = 5{x^2} - 1 + 3x + {x^2} - 5{x^3}\\F\left( x \right) = - 5{x^3} + \left( {5{x^2} + {x^2}} \right) + 3x - 1\\F\left( x \right) = - 5{x^3} + 6{x^2} + 3x - 1\end{array}\) Thu gọn \(G\left( x \right):\) \(\begin{array}{l}G\left( x \right) = 2 - 3{x^3} + 6{x^2} + 5x - 2{x^3} - x.\\G\left( x \right) = \left( { - 3{x^3} - 2{x^3}} \right) + 6{x^2} + \left( {5x - x} \right) + 2\\G\left( x \right) = - 5{x^3} + 6{x^2} + 4x + 2\end{array}\) b) Tính \(M\left( x \right)\) \(\begin{array}{l}M\left( x \right) = F\left( x \right) - G\left( x \right)\\M\left( x \right) = \left( { - 5{x^3} + 6{x^2} + 3x - 1} \right) - \left( { - 5{x^3} + 6{x^2} + 4x + 2} \right)\\M\left( x \right) = - 5{x^3} + 6{x^2} + 3x - 1 + 5{x^3} - 6{x^2} - 4x - 2\\M\left( x \right) = \left( { - 5{x^3} + 5{x^3}} \right) + \left( {6{x^2} - 6{x^2}} \right) + \left( {3x - 4x} \right) + \left( { - 1 - 2} \right)\\M\left( x \right) = \,\, - x - 3\end{array}\) Tìm nghiệm của đa thức \(M\left( x \right)\): Ta có: \(M\left( x \right) = - x - 3 = 0 \Leftrightarrow x = - 3\) Vậy \(x = - 3\) là nghiệm của đa thức \(M\left( x \right)\). c) Ta có: \(\begin{array}{l}N\left( x \right) + F\left( x \right) = - G\left( x \right)\\ \Rightarrow N\left( x \right) = - F\left( x \right) - G\left( x \right) = - \left[ {F\left( x \right) + G\left( x \right)} \right]\end{array}\) Trong đó: \(F\left( x \right) = - 5{x^3} + 6{x^2} + 3x - 1\) \(G\left( x \right) = - 5{x^3} + 6{x^2} + 4x + 2\) \(\begin{array}{l} \Rightarrow F\left( x \right) + G\left( x \right)\\ = \left( { - 5{x^3} + 6{x^2} + 3x - 1} \right) + \left( { - 5{x^3} + 6{x^2} + 4x + 2} \right)\\ = - 10{x^3} + 12{x^2} + 7x + 1\end{array}\) \(\begin{array}{l} \Rightarrow N\left( x \right) = - \left[ {F\left( x \right) + G\left( x \right)} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \left( { - 10{x^3} + 12{x^2} + 7x + 1} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 10{x^3} - 12{x^2} - 7x - 1\end{array}\) Vậy \(N\left( x \right) = 10{x^3} - 12{x^2} - 7x - 1\). Câu 4: Phương pháp: + Sử dụng các cách chứng minh hai tam giác bằng nhau. + Mối quan hệ giữa góc và cạnh trong tam giác (Cạnh đối diện với góc lớn hơn thì lớn hơn). + Mối quan hệ giữa ba cạnh trong tam giác. Bất đẳng thức trong tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn cạnh còn lại. + Tính chất đường trung trực của một đoạn thẳng: Mọi điểm nằm trên đường trung trực của đoạn thẳng cách đều hai đầu mút của đoạn thẳng đó. Cách giải: a) Xét \(\Delta ABD\)và \(\Delta HBD\)có: + \(\angle A = \angle H = {90^o}{\rm{ }}\left( {gt} \right)\) + Cạnh BD chung. + \(\angle ABD = \angle HBD{\rm{ }}\left( {gt} \right)\) \( \Rightarrow \)\(\Delta ABD = \Delta HBD\) (cạnh huyền – góc nhọn) (đpcm). b) + Do \(\Delta ABD = \Delta HBD\)\( \Rightarrow \left\{ \begin{array}{l}AB = BH\\AD = DH\end{array} \right.\)\( \Rightarrow \)\(BD\)là đường trung trực của \(AH\)(đpcm) + Ta có: \(AD = DH\) (1) Mà \(\Delta DHC\)vuông tại H \( \Rightarrow DH < DC\)(cạnh góc vuông <cạnh huyền) (2) Từ (1) và (2), suy ra \(AD < DC\) (đpcm). c) * Chứng minh \(K,D,H\)thẳng hàng: Xét \(\Delta AKD\)và \(\Delta HCD\)có: + \(AK = CH\) (gt) + \(\angle A = \angle H = {90^o}{\rm{ }}\left( {gt} \right)\) + \(AD = DH\) (theo b) \( \Rightarrow \)\(\Delta AKD = \Delta HCD\) (c.g.c) \( \Rightarrow \angle ADK = \angle HDC\)(hai góc tương ứng) (3) Mặt khác \(\angle HDC + \angle HDA = \angle ADC = {180^o}\) (4) Từ (3) và (4) \(\angle AKD + \angle HDA = {180^o}\) \( \Rightarrow DK,DH\)là hai tia đối nhau. \( \Rightarrow K,D,H\)thẳng hàng (đpcm) * Chứng minh \(BD \bot KC\) Xét \(\Delta KBC\)có: \(\left\{ \begin{array}{l}KB = KA + AB\\CB = CH + HB\end{array} \right.\) Mà \(KA = CH;AB = HB\) \( \Rightarrow KB = CB\). \( \Rightarrow \Delta KBC\)cân tại \(B\) Vì \(BD\)là tia phân giác của góc \(B\)nên suy ra \(BD\)đồng thời là đường cao trong \(\Delta KBC\)ứng với cạnh \(KC\). \( \Rightarrow BD \bot KC\) (đpcm). d) Chứng minh rằng: \(2\left( {AD + AK} \right) > CK\) Xét \(\Delta AKD\), ta có: \(AD + AK > KD \Rightarrow 2\left( {AD + AK} \right) > 2KD\) (mối quan hệ giữa ba cạnh trong tam giác) (5) Xét \(\Delta KDC\), ta có: \(KD = DC\) (do \(\Delta AKD = \Delta HCD\)ở cmt) \(\begin{array}{l} \Rightarrow KD + DC > KC\\ \Leftrightarrow 2KD > KC{\rm{ (6)}}\end{array}\) Từ (5) và (6) \( \Rightarrow 2\left( {AD + AK} \right) > CK\) (đpcm) Bài 5. Phương pháp: Xét với \(x = - 1\), ta tìm được mối liên hệ của \(f\left( { - 1} \right)\) và \(f\left( 1 \right)\) Xét với \(x = 1\), ta tìm được \(f\left( 1 \right)\). Cách giải: + Với \(x = - 1\), ta có: \(f\left( { - 1} \right) + \left( { - 1} \right).f\left( 1 \right) = - 1 + 1\) \(\begin{array}{l} \Rightarrow f\left( { - 1} \right) - f\left( 1 \right) = 0\\ \Rightarrow f\left( { - 1} \right) = f\left( 1 \right)\end{array}\) + Với \(x = 1\), ta có: \(f\left( 1 \right) + 1.f\left( { - 1} \right) = 1 + 1\) \( \Rightarrow f\left( 1 \right) + f\left( { - 1} \right) = 2\) Suy ra, \(f\left( 1 \right) + f\left( 1 \right) = 2\) \(\begin{array}{l} \Rightarrow 2f\left( 1 \right) = 2\\ \Rightarrow f\left( 1 \right) = 1\end{array}\) Vậy \(f\left( 1 \right) = 1\).
|