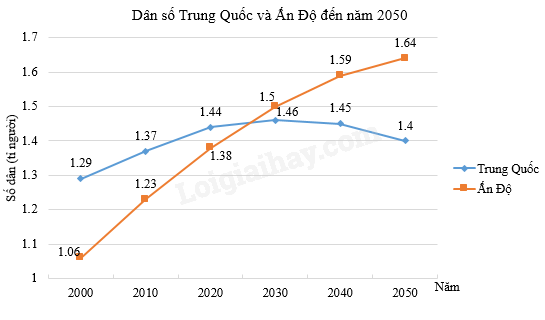
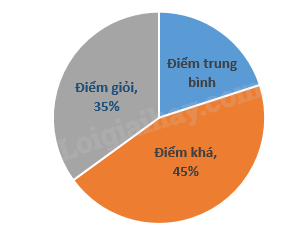
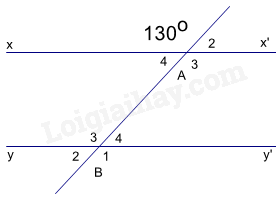
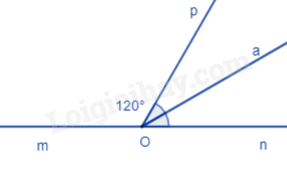
Đề cương ôn tập học kì 1 Toán 7 - Kết nối tri thứcTải vềA. NỘI DUNG ÔN TẬP Đại số Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... A. NỘI DUNG ÔN TẬPĐại số1. Số hữu tỉ- Cộng, trừ, nhân, chia số hữu tỉ 2. Số thực- Số vô tỉ - Căn bậc hai số học - Số thực Hình học1. Góc và đường thẳng song song- Góc ở vị trí đặc biệt - Tia phân giác của một góc 2. Tam giác bằng nhau- Tổng các góc trong một tam giác - Các trường hợp bằng nhau của hai tam giác: + Cạnh – cạnh – cạnh + Cạnh – góc – cạnh + Góc – cạnh – góc - Các trường hợp bằng nhau của hai tam giác vuông: + Hai cạnh góc vuông + Cạnh góc vuông – góc nhọn + Cạnh huyền – góc nhọn + Cạnh huyền – cạnh góc vuông - Tam giác cân – đường trung trực của đoạn thẳng Thống kê- Các loại biểu đồ: Biểu đồ quạt tròn, biểu đồ đoạn thẳng. B. BÀI TẬPĐề bàiI. Phần trắc nghiệmCâu 1: Khẳng định sai là: A. \(\sqrt {25} \in I\). B. \(8,\left( {45} \right) \in \mathbb{Q}\). C. \(\frac{{20}}{5} \in \mathbb{Z}\). D. \(\sqrt 7 \in I\). Câu 2: Kết quả của phép tính \(13,5.\frac{{ - 9}}{8} + 2,5.\frac{{ - 9}}{8}\) là: A. \( - 18\). B. \( - 15\). C. \( - 9\). D. \(\frac{{ - 8}}{9}\). Câu 3: Cho \(\left| {x - 1} \right| = \frac{4}{5}\). Tổng tất cả các giá trị của x thỏa mãn là: A. 0. B. 1. C. 2. D. 3. Câu 4: Kết quả của phép tính \(\left| {\frac{{ - 5}}{7}} \right|:\frac{5}{{14}}\) bằng : A. \(0\). B. \(\frac{{25}}{{98}}\). C. \(2\). D. \( - 2\). Câu 5: Kết quả của phép tính \(\frac{3}{4} - 25\% {\left( {\frac{{ - 1}}{2}} \right)^2}\) bằng : A. \(\frac{1}{8}\). B. \( - \frac{1}{8}\). C. \(0,25\). D. \(\frac{{11}}{{16}}\). Câu 6: Cho \(1 - {\left( {x + \frac{1}{3}} \right)^2} = \frac{5}{9}\). Số các giá trị âm của x thỏa mãn là : A. 0. B. 1. C. 2. D. 3. Câu 7: Nếu \(\sqrt x = 4\) thì \({x^2}\) bằng : A. 2. B. 4. C. 16. D. 256. Câu 8: Biết \({x^2} = 2\). Số các giá trị của x thỏa mãn là: A. 0. B. 1. C. 2. D. 3. Câu 9: Biết \(\left( {{x^2} + 1} \right)\left( {x - 3} \right) \le 0\). Số giá trị nguyên dương của x thỏa mãn là : A. 1. B. 2. C. 3. D. 4. Câu 10: Kết quả của phép tính 118:3 được làm tròn với độ chính xác 0,005 là: A. 39,34. B. 39,33. C. 39,334. D. 39,333. Câu 11: Kết quả của phép tính \(\sqrt {25 - 16} \) bằng: A. 1. B. 3. C. 9. D. 81. Câu 12: Khẳng định nào sau đây đúng? A. \(2 < \sqrt 3 \). B. \(\sqrt {{{\left( { - 3} \right)}^2}} = - 3\). C. \(\sqrt {4 + 9} = \sqrt 4 + \sqrt 9 \). D. \(7 > \sqrt {48} \). Câu 13: “Mức độ thường xuyên tập thể dục buổi sáng của các bạn trong lớp (rất thường xuyên, thường xuyên, không thường xuyên)”. Phương pháp thu thập dữ liệu nào là hợp lí? A. Lập bảng câu hỏi. B. Quan sát các bạn ở trên lớp. C. Phỏng vấn từng bạn. Câu 14: Dữ liệu thu được dưới đây thuộc loại nào? “Mức độ thường xuyên tập thể dục buổi sáng của các bạn trong lớp (rất thường xuyên, thường xuyên, không thường xuyên)”. A. Số liệu. B. Dữ liệu không phải là số (có thể sắp thứ tự). C. Dữ liệu không phải là số (không thể sắp thứ tự). Câu 15: Một cửa hàng bán nước hoa quả đã khảo sát về loại nước mà khách hàng ưu chuộng và thu được bảng dữ liệu sau: Từ bảng thống kê trên, hãy cho biết: a) Có bao nhiêu người tham gia cuộc khảo sát? A. 12 người. B. 20 người. C. 37 người. D. 47 người. b) Loại nước nào ít người ưa chuộng nhất? A. Nước cam. B. Nước dừa. C. Nước chanh. D. Nước ổi. c) Loại nước nào được nhiều nười ưa chuộng nhất? A. Nước cam. B. Nước dừa. C. Nước chanh. D. Nước ổi. Câu 16: Kết quả kiểm tra môn Toán của học sinh lớp 7A được cho trong bảng sau:
Từ bảng thống kê trên, hãy cho biết: a) Lớp 7A có bao nhiêu học sinh? A. 40 học sinh. B. 42 học sinh. C. 43 học sinh. D. 44 học sinh. b) Số học sinh đạt điểm 6 là bao nhiêu? A. 6 học sinh. B. 12 học sinh. C. 8 học sinh. D. 5 học sinh. c) Điểm nào được nhiều học sinh đạt nhất? A. Điểm 6. B. Điểm 7. C. Điểm 8. D. Điểm 9. Câu 17: Biểu đồ dưới đây cho biết số dân và dự báo quy mô dân số của Trung Quốc và Ấn Độ đến năm 2050.
Đến khoảng năm nào dân số Trung Quốc bằng với dân số Ấn Độ? A. Năm 2022 hoặc 2023. B. Năm 2025 hoặc 2026. C. Năm 2020. D. Năm 2030. Câu 18: Kết quả điểm kiểm tra cuối kì môn Toán của trường THCS được biểu thị trong biểu đồ hình quạt tròn dưới đây.
a) Tỉ lệ phần trăm học sinh đạt điểm trung bình so với toàn trường là: A. 10%. B. 20%. C. 30%. D. 40%. b) Biết trường có 400 học sinh. Số học sinh đạt điểm khá là: A. 140. B. 180. C. 240. D. 280. Câu 19: Cho hình vẽ, hãy chọn kết quả đúng trong các kết quả sau:
a) Số đo của \(\widehat {{B_3}}\) là: A. \({50^0}\). B. \({100^0}\). C. \({130^0}\). D. \({30^0}\). b) Hai góc bù nhau là: A. \(\widehat {{A_3}}\) và \(\widehat {{B_3}}\). B. \(\widehat {{A_4}}\) và \(\widehat {{B_2}}\). C. \(\widehat {{A_3}}\) và \(\widehat {{B_4}}\). D. \(\widehat {{A_2}}\) và \(\widehat {{B_4}}\). Câu 20: Cho đường thẳng mn, Oa là a là tia phân giác của góc pOn, biết \(\widehat {mOp} = {120^0}\). Số đo của góc aOn là:
A. \({40^0}\). B. \({60^0}\). C. \({30^0}\). D. \({25^0}\). Câu 21: Trong hình vẽ bên, có m // n, \(\widehat {{A_1}} = {85^0}\). Số đo góc B1 là:
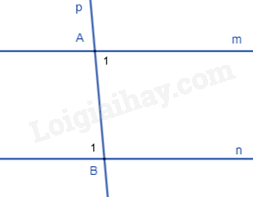
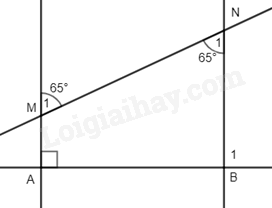
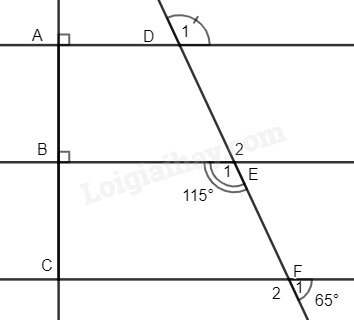
A. \({85^0}\). B. \({98^0}\). C. \({82^0}\). D. \({95^0}\). Câu 22: Cho hình vẽ dưới đây, biết \(BC{\rm{//}}DE;\) \(DC\) là tia phân giác của \(\widehat {BDE}\), số đo \(\widehat {EDB}\) là
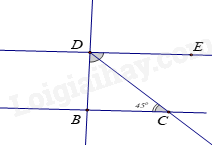
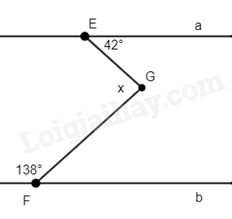
A. \(60^\circ \). B. \(90^\circ \). C. \(45^\circ \). D. \(135^\circ \). Câu 23: Cho hình vẽ, khẳng định nào sau đây là sai
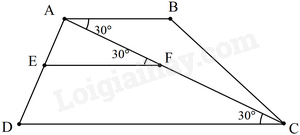
A. \(AB{\rm{//}}CD\). B. \(AB{\rm{//}}EF\). C. \(CD{\rm{//}}EF\). D. \(AB{\rm{//}}DE\). Câu 24: Cho định lí: “Nếu \(Ax,\)\(By\) là hai tia phân giác của hai góc đồng vị trong tạo bởi một đường thẳng cắt hai đường thẳng song song thì \(Ax\) song song với \(By\)”. Kết luận của định lí trên là A. Nếu \(Ax,\)\(By\) là hai tia phân giác của hai góc đồng vị trong tạo bởi một đường thẳng cắt hai đường thẳng song song. B. \(Ax\) song song với \(By\). C. \(Ax,\)\(By\) là hai tia phân giác của hai góc đồng vị. D. Nếu \(Ax,\)\(By\) là hai tia phân giác của hai góc đồng vị tạo bởi một đường thẳng cắt hai đường thẳng song song thì \(Ax\)song song với \(By\). Câu 25: Cho định lí: “Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cắt đường thẳng còn lại”. Giả thiết của định lí là A. Nếu một đường thẳng cắt một trong hai đường thẳng song song. B. Nếu một đường thẳng cắt một trong hai đường thẳng. C. Nó cắt đường thẳng còn lại. D. Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cắt đường thẳng còn lại. Câu 26: Cho các khẳng định sau 1. Hai góc đối đỉnh thì bằng nhau. 2. Hai góc bằng nhau thì đối đỉnh. 3. Nếu \(M\) là trung điểm của đoạn thẳng \(AB\) thì \(MA{\rm{ }} = {\rm{ }}MB\). 4. Nếu \(MA{\rm{ }} = {\rm{ }}MB\) thì \(M\) là trung điểm của đoạn thẳng \(AB\). Số các khẳng định đúng là A. 1. B. 2. C. 3. D. 4. Câu 27: Cho ABC là tam giác vuông sao cho \(\widehat A > \widehat B > \widehat C\). Câu nào dưới đây là sai? A. \(\widehat A = {90^0}\). B. \(\widehat B > {45^0}\). C. \(\widehat C < {45^0}\). D. \(\widehat B + \widehat C > \widehat A\). Câu 28. Dạng phát biểu khác của “Tiên đề Ơ-clit” là: A. Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó. B. Qua một điểm ở ngoài một đường thẳng có vô số đường thẳng song song với đường thẳng đó. C. Qua một điểm ở ngoài một đường thẳng có ít nhất một đường thẳng song song với đường thẳng đó. D. Qua một điểm ở ngoài một đường thẳng, có một đường thẳng song song với đường thẳng đó. Câu 29: Cho tam giác ABC có: \(\widehat A = \widehat B + \widehat C\). Câu nào dưới đây là đúng? A. Tam giác ABC vuông. B. \(\widehat B\) là góc tù. C. \(\widehat A\) là góc nhọn. D. \(\widehat C > {60^0}\). Câu 30: Cho \(\Delta ABC\) và \(\Delta DEF\) có AB = DE, BC = DF, CA = EF. Câu nào dưới đây là đúng? A. \(\Delta ABC = \Delta EDF\). B. \(\Delta ABC = \Delta DEF\). C. \(\Delta ABC = \Delta FED\). D. \(\Delta ABC = \Delta EFD\). Câu 31: Cho \(\Delta ABC\) và \(\Delta MNP\) có AB = MN, AC = NP, \(\widehat {CAB} = \widehat {MNP}\). Cách viết nào dưới đây đúng? A. \(\Delta ABC = \Delta NMP\left( {g.c.g} \right)\). B. \(\Delta ABC = \Delta MNP\left( {c.g.c} \right)\). C. \(\Delta ABC = \Delta NMP\left( {c.g.c} \right)\). D. \(\Delta ABC = \Delta MNP\left( {c.g.c} \right)\). Câu 32: Cho \(\Delta ABC = \Delta DEF\) và \(\Delta DEF = \Delta NMP\). Câu nào dưới đây là đúng? A. \(\Delta MNP = \Delta CAB\). B. \(\Delta MNP = \Delta ABC\). C. \(\Delta MNP = \Delta BCA\). D. \(\Delta MNP = \Delta BAC\). Câu 33: Cho tam giác ABC có chu vi bằng 45cm và AB = 10cm. Cho \(\Delta ABC = \Delta MNP\) và NP = 15cm. Câu nào dưới đây đúng? A. \(MP = 20cm\). B. \(BC = 20cm\). C. \(MN = 20cm\). D. \(AC = 15cm\). Câu 34: Cho tam giác ABC là tam giác cân có \(\widehat B = {100^0}\). Câu nào dưới đây đúng? A. \(AB = AC\). B. \(\widehat A = {100^0}\). C. \(\widehat C = {50^o}\). D. Tam giác cân tại đỉnh B. Câu 35: Cho \(\Delta ABC = \Delta DEF\). Điều nào dưới đây suy ra tam giác ABC cân tại đỉnh A? A. Tam giác DEF cân. B. AB = EF. C. \(\widehat C = \widehat E\). D. \(\widehat B = \widehat D\). II. Phần tự luậnBài 1. Tính theo cách hợp lý (nếu có thể): a) \(\frac{5}{{15}} + \frac{{14}}{{25}} - \frac{4}{3} + \frac{{11}}{{25}}\). b) \(\frac{5}{{20}} + 1\frac{7}{{11}} - 25\% - \left( {\frac{{18}}{{11}} - \frac{4}{9}} \right)\). c) \( - \frac{3}{4}.\frac{{12}}{{ - 5}}.\left( { - \frac{{25}}{6}} \right)\). d) \(2\frac{1}{9}.\frac{2}{3} + 15\frac{8}{9}.\frac{2}{3}\). e) \(\left( {\frac{{ - 2}}{3} + \frac{3}{{13}}} \right):\frac{7}{8} + \left( {\frac{{ - 1}}{3} + \frac{{10}}{{13}}} \right):\frac{7}{8}\). f) \(3:{\left( {\frac{{ - 3}}{2}} \right)^2} + \frac{1}{9}.\sqrt {36} + 0,75\). g) \(\frac{{{{\left( { - 1} \right)}^7}}}{{15}} + {\left( { - \frac{2}{3}} \right)^2}:2\frac{2}{3} - \left| { - \frac{5}{6}} \right|\). h) \(5:{\left( { - \frac{5}{2}} \right)^2} + \frac{2}{{15}}.\sqrt {\frac{9}{4}} - {\left( { - 2018} \right)^0} + 0,25\). Bài 2. Tìm x, biết: a) \(\frac{2}{3} + x = - \frac{1}{{12}}\) b) \(\frac{5}{{11}}x + 4 = 6\frac{1}{{11}}\) c) \({\left( {2x + 1} \right)^2} = \frac{{36}}{{25}}\) d) \({\left( {3x - 1} \right)^3} = - \frac{1}{{27}}\) e) \(\left| {\frac{1}{2}x - \frac{3}{4}} \right| - 2 = - \frac{3}{2}\) f) \(\left( {\frac{{15}}{4} - 5x} \right)\left( {9{x^2} - 4} \right) = 0\) g) \(\sqrt {x - 2} + \frac{1}{3} = 1\) với \(x \ge 2\) h) \({7^{2x}} + {7^{2x + 3}} = 344\) i) \(\frac{2}{{x + 3}} - \frac{1}{3} = \frac{{ - 5}}{{12}}\) với \(x \ne - 3\) j) \(\frac{x}{3} = \frac{{12}}{x}\) Bài 3. An đã hỏi một số bạn trong trường về hoạt động chiếm nhiều thời gian nhất trong tuần đầu tháng 6 vừa qua và thu được dữ liệu sau (D: đi du lịch, C: chơi thể thao, H: học thêm, L: làm việc nhà) HDHDDCDDHDCDCCDHDHDCDDCLDCLDLDLDDLCCDDCD a) An đã dụng phương pháp thu thập dữ liệu nào: quan sát, làm thí nghiệm, lập bảng hỏi hay phỏng vấn? b) Dữ liệu thu thập được thuộc loại nào? c) Hoàn thiện bảng thống kê sau vào vở.
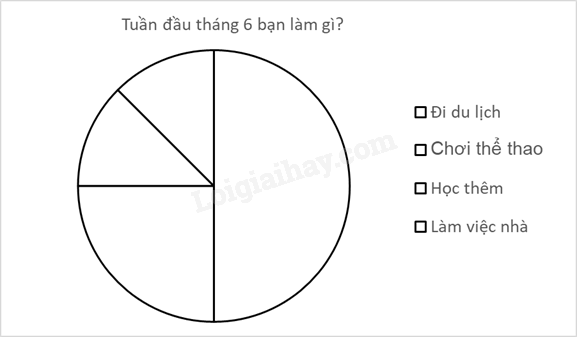
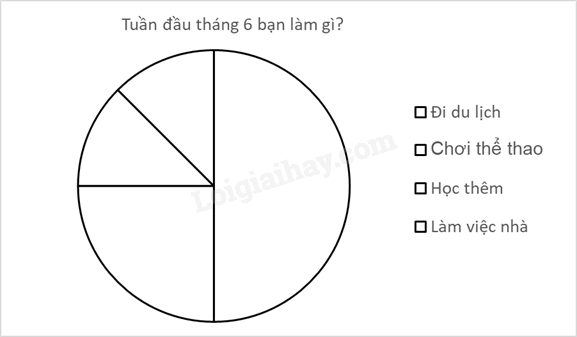
d) Hoàn thiện biểu đồ hình quạt tròn vào vở.
Bài 4. Minh làm bài kiểm tra trình độ tiếng Anh trên mạng Internet 6 lần và ghi lại kết quả (tỉ lệ số câu đúng) như sau:
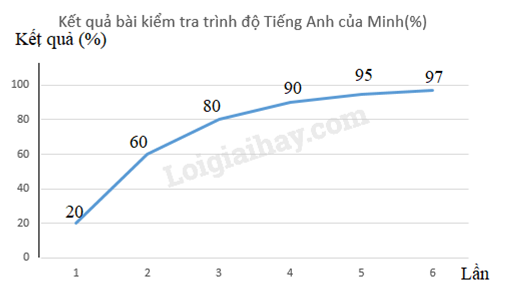
a) Vẽ biểu đồ đoạn thẳng biểu diễn bảng số liệu trên. b) Nhận xét sự tiến bộ của Minh sau mỗi lần làm bài. Bài 5. Nhà trường vận động mỗi bạn tặng một món quà cho các bạn học sinh vùng lũ lụt. Biểu đồ sau đây biểu diễn tỉ lệ học sinh lớp 7A tặng các món quà khác nhau. a) Từ biểu đồ, em hãy lập bảng thống kê về tỉ lệ học sinh lớp 7A tặng các món quà khác nhau. b) Lớp 7A có 40 học sinh. Tính số học tinh tặng từng loại món quà. Bài 6. Cho hình vẽ 5, \(\widehat {{M_1}} = \widehat {{N_1}} = {65^0}\). Tính \(\widehat {{B_1}}\). Bài 7. Cho hình vẽ 6, biết a // b. Tính số đo x. Bài 8. Cho hình vẽ 7. Tính \(\widehat {AOB}\). Bài 9. Cho hình vẽ 8. a) Chứng minh BE // CF. b) Tính \(\widehat {{D_1}}\).
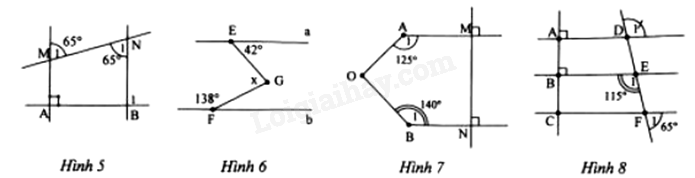
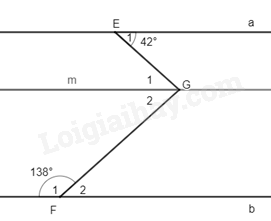
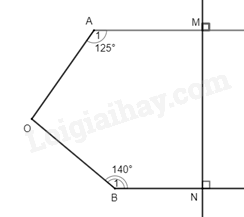
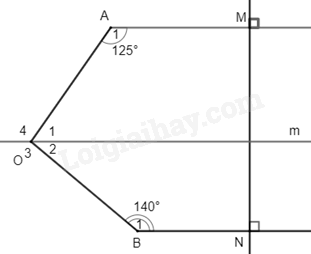
Bài 10. Cho \(\Delta ABC\) vuông tại A có \(AB > AC\). Kẻ \(AH \bot BC\) ( H thuộc BC). Lấy điểm D thuộc tia đối của tia HA sao cho \(HD = HA\). a) Chứng minh rằng \(\Delta CAH = \Delta CDH\) và tia CB là tia phân giác của \(\widehat {ACD}\). b) Qua D kẻ một đường thẳng song song với AC cắt BC tại M và cắt AB tại K. Chứng minh \(\Delta CHA = \Delta MHD\) và AD là đường trung trực của CM. c) Kẻ \(BN \bot AM\) ( N thuộc tia AM). Chứng minh B, N, D thẳng hàng. Bài 11. Cho \(\Delta ABC\) có \(AB < AC\). Tia phân giác \(\hat A\) cắt cạnh BC tại I. Trên cạnh AC lấy điểm D sao cho \(AD = AB\). a) Chứng minh rằng \(BI = ID\). b) Tia DI cắt tia AB tại E. Chứng minh \(\Delta IBE = \Delta IDC\). c) Chứng minh BD // EC. d) Cho \(\widehat {ABC} = 2.\widehat {ACB}\). Chứng minh \(AB + BI = AC\). Bài 12. Cho \(\Delta ABC\) vuông tại A. Gọi M là trung điểm của BC. Phân giác \(\widehat {ABC}\) cắt AC tại I. Biết \(BI \bot AM\) tại H. a) Chứng minh \(IA = IM\). b) Tính các góc của \(\Delta BIC\). c) Trên tia đối của tia HB lấy điểm K sao cho \(HK = HB\). Chứng minh rằng \(\Delta AIB = \Delta KIC\). Bài 13*. a) Tính GTNN của biểu thức \(A = 2 + 3\sqrt {{x^2} + 1} \); \(B = \left| {x - 1} \right| + \left| {x - 3} \right|\) b) Tính GTLN của biểu thức \(C = \frac{{5{x^2} + 12}}{{{x^2} + 2}}\); \(D = 4 - \left| {5x - 2} \right| - \left| {3y + 12} \right|\) Bài 14*. Cho \(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}};B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\). So sánh A và B.
Lời giải chi tiếtI. Trắc nghiệm
II. Phần tự luậnBài 1. Tính theo cách hợp lý (nếu có thể): a) \(\frac{5}{{15}} + \frac{{14}}{{25}} - \frac{4}{3} + \frac{{11}}{{25}}\). b) \(\frac{5}{{20}} + 1\frac{7}{{11}} - 25\% - \left( {\frac{{18}}{{11}} - \frac{4}{9}} \right)\). c) \( - \frac{3}{4}.\frac{{12}}{{ - 5}}.\left( { - \frac{{25}}{6}} \right)\). d) \(2\frac{1}{9}.\frac{2}{3} + 15\frac{{8}}{{9}}.\frac{2}{3}\). e) \(\left( {\frac{{ - 2}}{3} + \frac{3}{{13}}} \right):\frac{7}{8} + \left( {\frac{{ - 1}}{3} + \frac{{10}}{{13}}} \right):\frac{7}{8}\). f) \(3:{\left( {\frac{{ - 3}}{2}} \right)^2} + \frac{1}{9}.\sqrt {36} + 0,75\). g) \(\frac{{{{\left( { - 1} \right)}^7}}}{{15}} + {\left( { - \frac{2}{3}} \right)^2}:2\frac{2}{3} - \left| { - \frac{5}{6}} \right|\). h) \(5:{\left( { - \frac{5}{2}} \right)^2} + \frac{2}{{15}}.\sqrt {\frac{9}{4}} - {\left( { - 2018} \right)^0} + 0,25\). Phương pháp - Thực hiện các phép toán với các số hữu tỉ - Tính lũy thừa của một số hữu tỉ - Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x > 0\\ - x\,khi\,x < 0\\0\,khi\,x = 0\end{array} \right.\) - Tính toán căn bậc hai của một số thực Lời giải a) \(\frac{5}{{15}} + \frac{{14}}{{25}} - \frac{4}{3} + \frac{{11}}{{25}}\) \(\begin{array}{l} = \frac{1}{3} + \frac{{14}}{{25}} - \frac{4}{3} + \frac{{11}}{{25}}\\ = \left( {\frac{1}{3} - \frac{4}{3}} \right) + \left( {\frac{{14}}{{25}} + \frac{{11}}{{25}}} \right)\\ = - 1 + 1\\ = 0\end{array}\) b) \(\frac{5}{{20}} + 1\frac{7}{{11}} - 25\% - \left( {\frac{{18}}{{11}} - \frac{4}{9}} \right)\) \(\begin{array}{l} = \frac{1}{4} + \frac{{18}}{{11}} - \frac{1}{4} - \frac{{18}}{{11}} + \frac{4}{9}\\ = \left( {\frac{1}{4} - \frac{1}{4}} \right) + \left( {\frac{{18}}{{11}} - \frac{{18}}{{11}}} \right) + \frac{4}{9}\\ = \frac{4}{9}\end{array}\) c) \( - \frac{3}{4}.\frac{{12}}{{ - 5}}.\left( { - \frac{{25}}{6}} \right)\) \(\begin{array}{l} = \frac{{ - 3.12.\left( { - 25} \right)}}{{4.\left( { - 5} \right).6}}\\ = \frac{{{{3.3.4.5}^2}}}{{4.\left( { - 5} \right).2.3}}\\ = \frac{{3.5}}{{ - 2}}\\ = \frac{{ - 15}}{2}\end{array}\) d) \(2\frac{1}{9}.\frac{2}{3} + 15\frac{8}{9}.\frac{2}{3}\) \(\begin{array}{l} = \left( {2\frac{1}{9} + 15\frac{8}{9}} \right).\frac{2}{3}\\ = \left[ {\left( {2 + 15} \right) + \left( {\frac{1}{9} + \frac{8}{9}} \right)} \right].\frac{2}{3}\\ = \left( {17 + 1} \right).\frac{2}{3}\\ = 18.\frac{2}{3}\\ = 12\end{array}\) e) \(\left( {\frac{{ - 2}}{3} + \frac{3}{{13}}} \right):\frac{7}{8} + \left( {\frac{{ - 1}}{3} + \frac{{10}}{{13}}} \right):\frac{7}{8}\) \(\begin{array}{l} = \left( {\frac{{ - 2}}{3} + \frac{3}{{13}} + \frac{{ - 1}}{3} + \frac{{10}}{{13}}} \right):\frac{7}{8}\\ = \left[ {\left( {\frac{{ - 2}}{3} + \frac{{ - 1}}{3}} \right) + \left( {\frac{3}{{13}} + \frac{{10}}{{13}}} \right)} \right]:\frac{7}{8}\\ = \left( { - 1 + 1} \right):\frac{7}{8}\\ = 0:\frac{7}{8}\\ = 0\end{array}\) f) \(3:{\left( {\frac{{ - 3}}{2}} \right)^2} + \frac{1}{9}.\sqrt {36} + 0,75\) \(\begin{array}{l} = 3:\frac{9}{4} + \frac{1}{9}.6 + \frac{3}{4}\\ = 3.\frac{4}{9} + \frac{6}{9} + \frac{3}{4}\\ = \frac{4}{3} + \frac{2}{3} + \frac{3}{4}\\ = 2 + \frac{3}{4}\\ = \frac{{11}}{4}\end{array}\) g) \(\frac{{{{\left( { - 1} \right)}^7}}}{{15}} + {\left( { - \frac{2}{3}} \right)^2}:2\frac{2}{3} - \left| { - \frac{5}{6}} \right|\) \(\begin{array}{l} = \frac{{ - 1}}{{15}} + \frac{4}{9}:\frac{8}{3} - \frac{5}{6}\\ = \frac{{ - 1}}{{15}} + \frac{4}{9}.\frac{3}{8} - \frac{5}{6}\\ = \frac{{ - 1}}{{15}} + \frac{1}{6} - \frac{5}{6}\\ = \frac{{ - 1}}{{15}} + \left( {\frac{1}{6} - \frac{5}{6}} \right)\\ = \frac{{ - 1}}{{15}} - \frac{2}{3}\\ = \frac{{ - 11}}{{15}}\end{array}\) h) \(5:{\left( { - \frac{5}{2}} \right)^2} + \frac{2}{{15}}.\sqrt {\frac{9}{4}} - {\left( { - 2018} \right)^0} + 0,25\) \(\begin{array}{l} = 5:\frac{{25}}{4} + \frac{2}{{15}}.\frac{3}{2} - 1 + \frac{1}{4}\\ = 5.\frac{4}{{25}} + \frac{1}{5} - 1 + \frac{1}{4}\\ = \frac{4}{5} + \frac{1}{5} - 1 + \frac{1}{4}\\ = 1 - 1 + \frac{1}{4}\\ = \frac{1}{4}\end{array}\) Bài 2. Tìm x, biết: a) \(\frac{2}{3} + x = - \frac{1}{{12}}\) b) \(\frac{5}{{11}}x + 4 = 6\frac{1}{{11}}\) c) \({\left( {2x + 1} \right)^2} = \frac{{36}}{{25}}\) d) \({\left( {3x - 1} \right)^3} = - \frac{1}{{27}}\) e) \(\left| {\frac{1}{2}x - \frac{3}{4}} \right| - 2 = - \frac{3}{2}\) f) \(\left( {\frac{{15}}{4} - 5x} \right)\left( {9{x^2} - 4} \right) = 0\) g) \(\sqrt {x - 2} + \frac{1}{3} = 1\) với \(x \ge 2\) h) \({7^{2x}} + {7^{2x + 3}} = 344\) i) \(\frac{2}{{x + 3}} - \frac{1}{3} = \frac{{ - 5}}{{12}}\) với \(x \ne - 3\) j) \(\frac{x}{3} = \frac{{12}}{x}\) Phương pháp - Sử dụng kiến thức chuyển vế, tính toán với số hữu tỉ - Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x > 0\\ - x\,khi\,x < 0\\0\,khi\,x = 0\end{array} \right.\) - Vận dụng kiến thức căn bậc hai của một số thực Lời giải a) \(\frac{2}{3} + x = - \frac{1}{{12}}\) \(\begin{array}{l}x = - \frac{1}{{12}} - \frac{2}{3}\\x = \frac{{ - 3}}{4}\end{array}\) Vậy nghiệm của phương trình là \(x = \frac{{ - 3}}{4}\). b) \(\frac{5}{{11}}x + 4 = 6\frac{1}{{11}}\) \(\begin{array}{l}\frac{5}{{11}}x = 6\frac{1}{{11}} - 4\\\frac{5}{{11}}x = 2\frac{1}{{11}}\\\frac{5}{{11}}x = \frac{{23}}{{11}}\\x = \frac{{23}}{{11}}:\frac{5}{{11}}\\x = \frac{{23}}{5}\end{array}\) Vậy nghiệm của phương trình là \(x = \frac{{23}}{5}\). c) \({\left( {2x + 1} \right)^2} = \frac{{36}}{{25}}\) \({\left( {2x + 1} \right)^2} = {\left( { \pm \frac{6}{5}} \right)^2}\) \( \Rightarrow 2x + 1 = \frac{6}{5}\) hoặc \(2x + 1 = - \frac{6}{5}\) TH1: \(2x + 1 = \frac{6}{5}\) \(\begin{array}{l}2x = \frac{6}{5} - 1\\2x = \frac{1}{5}\\x = \frac{1}{5}:2\\x = \frac{1}{{10}}\end{array}\) TH2: \(2x + 1 = - \frac{6}{5}\) \(\begin{array}{l}2x + 1 = - \frac{6}{5}\\2x = - \frac{6}{5} - 1\\2x = - \frac{{11}}{5}\\x = - \frac{{11}}{5}:2\\x = - \frac{{11}}{{10}}\end{array}\) Vậy nghiệm của phương trình là \(x \in \left\{ {\frac{1}{{10}}; - \frac{{11}}{{10}}} \right\}\). d) \({\left( {3x - 1} \right)^3} = - \frac{1}{{27}}\) \(\begin{array}{l}{\left( {3x - 1} \right)^3} = - \frac{1}{{27}}\\{\left( {3x - 1} \right)^3} = {\left( { - \frac{1}{3}} \right)^3}\\3x - 1 = - \frac{1}{3}\\3x = - \frac{1}{3} + 1\\3x = \frac{2}{3}\\x = \frac{2}{9}\end{array}\) Vậy nghiệm của phương trình là \(x = \frac{2}{9}\). e) \(\left| {\frac{1}{2}x - \frac{3}{4}} \right| - 2 = - \frac{3}{2}\) \(\begin{array}{l}\left| {\frac{1}{2}x - \frac{3}{4}} \right| - 2 = - \frac{3}{2}\\\left| {\frac{1}{2}x - \frac{3}{4}} \right| = - \frac{3}{2} + 2\\\left| {\frac{1}{2}x - \frac{3}{4}} \right| = \frac{1}{2}\end{array}\) \( \Rightarrow \frac{1}{2}x - \frac{3}{4} = \frac{1}{2}\) hoặc \(\frac{1}{2}x - \frac{3}{4} = - \frac{1}{2}\) TH1: \(\frac{1}{2}x - \frac{3}{4} = \frac{1}{2}\) \(\begin{array}{l}\frac{1}{2}x = \frac{1}{2} + \frac{3}{4}\\\frac{1}{2}x = \frac{5}{4}\\x = \frac{5}{4}:\frac{1}{2}\\x = \frac{5}{2}\end{array}\) TH2: \(\frac{1}{2}x - \frac{3}{4} = - \frac{1}{2}\) \(\begin{array}{l}\frac{1}{2}x = - \frac{1}{2} + \frac{3}{4}\\\frac{1}{2}x = \frac{1}{4}\\x = \frac{1}{4}:\frac{1}{2}\\x = \frac{1}{2}\end{array}\) Vậy nghiệm của phương trình là \(x \in \left\{ {\frac{5}{2};\frac{1}{2}} \right\}\). f) \(\left( {\frac{{15}}{4} - 5x} \right)\left( {9{x^2} - 4} \right) = 0\) \(\frac{{15}}{4} - 5x = 0\) hoặc \(9{x^2} - 4 = 0\) TH1: \(\frac{{15}}{4} - 5x = 0\) \(\begin{array}{l}5x = \frac{{15}}{4}\\x = \frac{3}{4}\end{array}\) TH2: \(9{x^2} - 4 = 0\) \(\begin{array}{l}9{x^2} = 4\\{x^2} = \frac{4}{9}\\x = \pm \frac{2}{3}\end{array}\) Vậy nghiệm của phương trình là \(x \in \left\{ { \pm \frac{2}{3};\frac{3}{4}} \right\}\). g) \(\sqrt {x - 2} + \frac{1}{3} = 1\) với \(x \ge 2\) \(\begin{array}{l}\sqrt {x - 2} = \frac{2}{3}\\x - 2 = {\left( {\frac{2}{3}} \right)^2}\\x - 2 = \frac{4}{9}\\x = \frac{{22}}{9}\end{array}\) Vậy nghiệm của phương trình là \(x = \frac{{22}}{9}\). h) \({7^{2x}} + {7^{2x + 3}} = 344\) \(\begin{array}{l}{7^{2x}} + {7^{2x}}{.7^3} = 344\\{7^{2x}} + {343.7^{2x}} = 344\\{7^{2x}}\left( {1 + 343} \right) = 344\\{7^{2x}}.344 = 344\\{7^{2x}} = 1\\{7^{2x}} = {7^0}\\2x = 0\\x = 0\end{array}\) Vậy nghiệm của phương trình là \(x = 0\). i) \(\frac{2}{{x + 3}} - \frac{1}{3} = \frac{{ - 5}}{{12}}\) với \(x \ne - 3\) \(\begin{array}{l}\frac{{2.12}}{{\left( {x + 3} \right).12}} - \frac{{4\left( {x + 3} \right)}}{{3.4\left( {x + 3} \right)}} = \frac{{ - 5\left( {x + 3} \right)}}{{12\left( {x + 3} \right)}}\\\frac{{24 - 4\left( {x + 3} \right)}}{{12\left( {x + 3} \right)}} = \frac{{ - 5\left( {x + 3} \right)}}{{12\left( {x + 3} \right)}}\\ \Rightarrow 24 - 4x - 12 = - 5x - 15\\ - 4x + 5x = - 15 + 12 - 24\\x = - 27\end{array}\) Vậy nghiệm của phương trình là \(x = - 27\). j) \(\frac{x}{3} = \frac{{12}}{x}\) (điều kiện: \(x \ne 0\)) \(\begin{array}{l}\frac{x}{3} - \frac{{12}}{x} = 0\\\frac{{{x^2} - 12.3}}{{3x}} = 0\\\frac{{{x^2} - 36}}{{3x}} = 0\\ \Rightarrow {x^2} - 36 = 0\\{x^2} = 36\end{array}\) \(x = 6\) hoặc \(x = - 6\) (thỏa mãn điều kiện) Vậy nghiệm của phương trình là \(x \in \left\{ { \pm 6} \right\}\). Bài 3. An đã hỏi một số bạn trong trường về hoạt động chiếm nhiều thời gian nhất trong tuần đầu tháng 6 vừa qua và thu được dữ liệu sau (D: đi du lịch, C: chơi thể thao, H: học thêm, L: làm việc nhà) HDHDDCDDHDCDCCDHDHDCDDCLDCLDLDLDDLCCDDCD a) An đã dụng phương pháp thu thập dữ liệu nào: quan sát, làm thí nghiệm, lập bảng hỏi hay phỏng vấn? b) Dữ liệu thu thập được thuộc loại nào? c) Hoàn thiện bảng thống kê sau vào vở.
d) Hoàn thiện biểu đồ hình quạt tròn vào vở.
Phương pháp Đọc dãy dữ liệu để trả lời câu hỏi. Lời giải a) An đã dùng phương pháp phỏng vấn để thu thập dữ liệu. b) Dữ liệu thu được là dữ liệu không là số, không thể sắp thứ tự. c) Trong dãy dữ liệu có 10 chữ cái C tức là có 10 bạn dành nhiều thời gian chơi thể thao. Tương tự, có 5 chữ cái H, 5 chữ cái L, 20 chữ cái D. Ta có bảng thống kê:
d) Biểu đồ hoàn thiện: Bài 4. Minh làm bài kiểm tra trình độ tiếng Anh trên mạng Internet 6 lần và ghi lại kết quả (tỉ lệ số câu đúng) như sau:
a) Vẽ biểu đồ đoạn thẳng biểu diễn bảng số liệu trên. b) Nhận xét sự tiến bộ của Minh sau mỗi lần làm bài. Phương pháp Biểu đồ đi lên biểu thị kết quả tăng dần theo thời gian. Lời giải a)
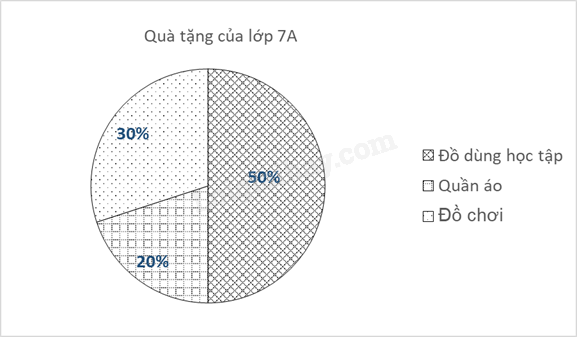
b) Minh có sự tiến bộ sau mỗi lần làm bài Từ lần kiểm tra thứ nhất đến lần kiểm tra thứ hai, Minh có sự tiến bộ nhiều nhất. Bài 5. Nhà trường vận động mỗi bạn tặng một món quà cho các bạn học sinh vùng lũ lụt. Biểu đồ sau đây biểu diễn tỉ lệ học sinh lớp 7A tặng các món quà khác nhau. a) Từ biểu đồ, em hãy lập bảng thống kê về tỉ lệ học sinh lớp 7A tặng các món quà khác nhau. b) Lớp 7A có 40 học sinh. Tính số học tinh tặng từng loại món quà. Phương pháp a) Quan sát biểu đồ để lập bảng thống kê. b) Tính m% của a, ta tính \(\frac{m}{{100}}.a\) Lời giải a) Ta có bảng thống kê về tỉ lệ học sinh lớp 7A tặng các món quà khác nhau như sau:
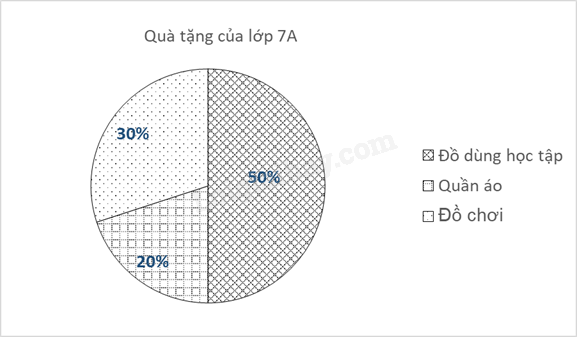
b) Số học sinh tặng đồ dùng học tập là: \(\frac{{50}}{{100}}.40 = 20\) (học sinh) Số học sinh tặng quần áo là: \(\frac{{20}}{{100}}.40 = 8\) (học sinh) Số học sinh tặng đồ chơi là: \(\frac{{30}}{{100}}.40 = 12\) (học sinh) Vậy có 20 học sinh tặng quà tặng là đồ dùng học tập, 8 học sinh tặng quà tặng là quần áo, 12 học sinh tặng quà tặng là đồ chơi. Bài 6. Cho hình vẽ 5, \(\widehat {{M_1}} = \widehat {{N_1}} = {65^0}\). Tính \(\widehat {{B_1}}\). Phương pháp Sử dụng dấu hiệu nhận biết hai đường thẳng song song. Tính chất của hai đường thẳng song song. Lời giải Ta có: \(\widehat {{M_1}} = \widehat {{N_1}} = {65^0}\). Mà hai góc này ở vị trí so le trong nên AM // BN. \( \Rightarrow \widehat {MAB} = \widehat {{B_1}}\) (hai góc đồng vị) \(\widehat {MAB} = {90^0} \Rightarrow \widehat {{B_1}} = {90^0}\). Bài 7. Cho hình vẽ 6, biết a // b. Tính số đo x. Phương pháp Kẻ đường thẳng đi qua G song song với a và b. Sử dụng tính chất của hai đường thẳng song song, hai góc kề bù. Lời giải Kẻ đường thẳng m đi qua G và song song với a và b. Khi đó \(\widehat {{E_1}} = \widehat {{G_1}} = {42^0}\) (hai góc so le trong) Ta có \(\widehat {{F_1}}\) và \(\widehat {{F_2}}\) là hai góc kề bù \( \Rightarrow \widehat {{F_1}} + \widehat {{F_2}} = {180^0}\) \( \Rightarrow \widehat {{F_2}} = {180^0} - \widehat {{F_1}} = {180^0} - {138^0} = {42^0}\) Vì m // b nên \(\widehat {{G_2}} = \widehat {{F_2}} = {42^0}\) (hai góc so le trong) Mà x = \(\widehat {{G_1}} + \widehat {{G_2}}\) \( \Rightarrow \widehat {{G_1}} + \widehat {{G_2}} = {42^0} + {42^0} = {84^0}\) Vậy \(x = {84^0}\). Bài 8. Cho hình vẽ 7. Tính \(\widehat {AOB}\). Phương pháp - Sử dụng dấu hiệu nhận biết hai đường thẳng song song. - Kẻ đường thẳng đi qua O song song với AM. - Sử dụng tính chất của hai đường thẳng song song, hai góc kề bù. Lời giải
Ta có: \(\widehat M = \widehat N = {90^0}\) (hai góc đồng vị) nên AM // BN. Qua O kẻ đường thẳng m song song với AM và BN, khi đó: \(\widehat {{A_1}} = \widehat {{O_4}} = {125^0};\widehat {{B_1}} = \widehat {{O_2}}\) (các cặp góc so le trong) Mà \(\widehat {{O_1}}\) và \(\widehat {{O_4}}\) là hai góc kề bù nên \(\widehat {{O_1}} + \widehat {{O_4}} = {180^0} \Rightarrow \widehat {{O_1}} = {55^0}\); \(\widehat {{O_2}}\) và \(\widehat {{O_3}}\) là hai góc kề bù nên \(\widehat {{O_2}} + \widehat {{O_3}} = {180^0} \Rightarrow \widehat {{O_2}} = {40^0}\). Ta có: \(\widehat {AOB} = \widehat {{O_1}} + \widehat {{O_2}} = {55^0} + {40^0} = {95^0}\). Vậy \(\widehat {AOB} = {95^0}\). Bài 9. Cho hình vẽ 8. a) Chứng minh BE // CF. b) Tính \(\widehat {{D_1}}\).
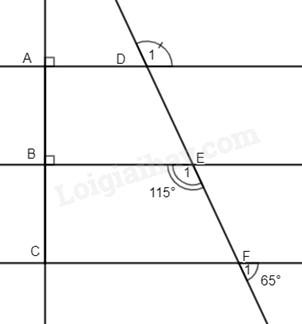
Phương pháp a) Sử dụng dấu hiệu nhận biết hai đường thẳng song song, hai góc kề bù. b) Sử dụng tính chất của hai đường thẳng song song, hai góc đối đỉnh. Lời giải
a) Ta có \(\widehat {{F_1}} + \widehat {{F_2}} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {{F_2}} = {180^0} - {65^0} = {115^0}\). Ta thấy: \(\widehat {{E_1}} = \widehat {{F_2}} = {115^0}\) Mà \(\widehat {{E_1}}\) và \(\widehat {{F_2}}\) là hai góc ở vị trí đồng vị nên BE // CF (đpcm) b) Ta có: \(\widehat A = \widehat B = {90^0}\). Mà \(\widehat A\) và \(\widehat B\) ở vị trí đồng vị nên AD // BE. \( \Rightarrow \widehat {{D_1}} = \widehat {{E_2}}\) (hai góc đồng vị). Mà \(\widehat {{E_2}} = \widehat {{E_1}} = {115^0}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {{D_1}} = {115^0}\). Vậy \(\widehat {{D_1}} = {115^0}\). Bài 10. Cho \(\Delta ABC\) vuông tại A có \(AB > AC\). Kẻ \(AH \bot BC\) ( H thuộc BC). Lấy điểm D thuộc tia đối của tia HA sao cho \(HD = HA\). a) Chứng minh rằng \(\Delta CAH = \Delta CDH\) và tia CB là tia phân giác của \(\widehat {ACD}\). b) Qua D kẻ một đường thẳng song song với AC cắt BC tại M và cắt AB tại K. Chứng minh \(\Delta CHA = \Delta MHD\) và AD là đường trung trực của CM. c) Kẻ \(BN \bot AM\) ( N thuộc tia AM). Chứng minh B, N, D thẳng hàng. Phương pháp a) Chứng minh \(\Delta CAH = \Delta CDH\) theo trường hợp hai cạnh góc vuông, suy ra cặp góc tương ứng bằng nhau suy ra tia CB là tia phân giác của \(\widehat {ACD}\). b) Dựa vào tính chất hai đường thẳng song song. Chứng minh \(\Delta CHA = \Delta MHD\) theo trường hợp góc – cạnh – góc. Chứng minh AD là đường trung trực: chứng minh \(AD \bot MC\) và \(MH = HC\). c) Chứng minh \(CD \bot BD,AM//CD \Rightarrow BN \equiv BD\) nên B, N, D thẳng hàng. Lời giải
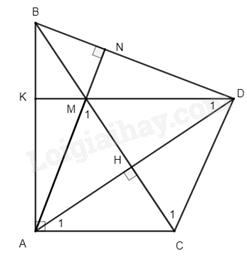
a) Xét tam giác \(\Delta CAH\) và \(\Delta CDH\) có: HA = HD (gt) \(\widehat {AHC} = \widehat {DHC} = {90^0}\) HC chung \( \Rightarrow \Delta CAH = \Delta CDH\) (hai cạnh góc vuông) (đpcm) \( \Rightarrow \widehat {ACH} = \widehat {DCH}\) (hai góc tương ứng) \( \Rightarrow CH\) là đường phân giác của \(\widehat {ACD}\) hay tia CB là tia phân giác của \(\widehat {ACD}\) (đpcm) b) Vì DM // AC nên \(\widehat {{A_1}} = \widehat {{D_1}}\) (hai góc so le trong) Xét \(\Delta CHA\) và \(\Delta MHD\) có: \(\widehat {{A_1}} = \widehat {{D_1}}\) (cmt) AH = HD (gt) \(\widehat {AHC} = \widehat {DHM}\left( { = {{90}^0}} \right)\) \( \Rightarrow \Delta CHA = \Delta MHD\) (g.c.g) (đpcm) \( \Rightarrow CH = HM\) (hai cạnh tương ứng) Mà \(AD \bot MC\) (gt) \( \Rightarrow \) AD là đường trung trực của CM (đpcm) c) Vì \(\Delta CAH = \Delta CDH\) nên AC = CD (hai cạnh tương ứng) Xét \(\Delta ABC\) và \(\Delta DBC\) có: AC = CD (cmt) \(\widehat {ACB} = \widehat {DCB}\) (BC là tia phân giác của góc ACD) BC chung \( \Rightarrow \Delta ABC = \Delta DBC\) (c.g.c) \( \Rightarrow \widehat {BAC} = \widehat {BDC} = {90^0}\) (hai góc tương ứng và \(\widehat {BAC} = {90^0}\)) hay \(CD \bot BD\). (1) Xét \(\Delta AHM\) và \(\Delta DHC\) có: AH = HD (gt) \(\widehat {AHM} = \widehat {DHC} = ({90^0})\) (hai góc đối đỉnh) MH = HC (cmt) \( \Rightarrow \Delta AHM = \Delta DHC\) (hai cạnh góc vuông) \( \Rightarrow \widehat {{M_1}} = \widehat {{C_1}}\) (hai góc tương ứng). Mà hai góc này ở vị trí so le trong \( \Rightarrow AM//CD\) (2) Từ (1) và (2) suy ra \(AM \bot BD\). Mà \(AM \bot BN\) (gt) \( \Rightarrow BN \equiv BD\) hay B, N, D thẳng hàng. (đpcm) Bài 11. Cho \(\Delta ABC\) có \(AB < AC\). Tia phân giác \(\hat A\) cắt cạnh BC tại I. Trên cạnh AC lấy điểm D sao cho \(AD = AB\). a) Chứng minh rằng \(BI = ID\). b) Tia DI cắt tia AB tại E. Chứng minh \(\Delta IBE = \Delta IDC\). c) Chứng minh BD // EC. d) Cho \(\widehat {ABC} = 2.\widehat {ACB}\). Chứng minh \(AB + BI = AC\). Phương pháp a) Chứng minh \(\Delta ABI = \Delta ADI\left( {c.g.c} \right) \Rightarrow BI = ID\) (hai cạnh tương ứng) b) Chứng minh \(\Delta IBE = \Delta IDC\) (g.c.g) c) Chứng minh tam giác IEC và tam giác IBD cân suy ra các góc bằng nhau. Chứng minh hai góc so le trong \(\widehat {{B_2}} = \widehat {{C_1}}\) suy ra BD // EC. d) Dựa vào định lí tổng ba góc trong tam giác, hai góc kề bù để chứng minh tam giác DCI cân tại I. Chứng minh \(AD = AB,DC = BI\) suy ra \(AB + BI = AC\) Lời giải
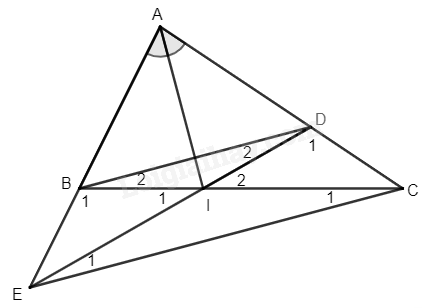
a) Xét \(\Delta ABI\) và \(\Delta ADI\) có: AB = AD (gt) \(\widehat {BAI} = \widehat {DAI}\) (AI là tia phân giác của \(\widehat A\)) AI chung \( \Rightarrow \Delta ABI = \Delta ADI\) (c.g.c) \( \Rightarrow BI = ID\) (hai cạnh tương ứng) (đpcm) b) Vì \(\Delta ABI = \Delta ADI\) nên \(\widehat {ABI} = \widehat {ADI}\) (hai góc tương ứng) \( \Rightarrow \widehat {{B_1}} = \widehat {{D_1}}\) (hai góc kề bù của \(\widehat {ABI}\) và \(\widehat {ADI}\)) Xét \(\Delta IBE\) và \(\Delta IDC\) có: \(\widehat {{B_1}} = \widehat {{D_1}}\) (cmt) BI = ID (cmt) \(\widehat {{I_1}} = \widehat {{I_2}}\) (hai góc đối đỉnh) \( \Rightarrow \Delta IBE = \Delta IDC\) (g.c.g) (đpcm) c) Ta có: \(\Delta IBE = \Delta IDC \Rightarrow IE = IC\) nên tam giác IEC cân tại I \( \Rightarrow \widehat {{E_1}} = \widehat {{C_1}} = \frac{{{{180}^0} - \widehat {EIC}}}{2}\). Ta có: IB = ID nên tam giác IBD cân tại I \( \Rightarrow \widehat {{B_2}} = \widehat {{D_2}} = \frac{{{{180}^0} - \widehat {BID}}}{2}\). Mà \(\widehat {BID} = \widehat {EIC}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {{B_2}} = \widehat {{C_1}}\). Mà hai góc này ở vị trí so le trong \( \Rightarrow BD//EC\) (đpcm) d) Ta có: \(\widehat {ABI} = \widehat {ADI}\) (cmt), mà \(\widehat {ADI} + \widehat {{D_1}} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {ABI} + \widehat {{D_1}} = {180^0} \Rightarrow 2\widehat {DCI} + \widehat {{D_1}} = {180^0}\) (vì \(\widehat {ABI} = \widehat {ABC},\widehat {DCI} = \widehat {ACB},\widehat {ABC} = 2.\widehat {ACB}\)) (1) Xét \(\Delta DCI\) có: \(\widehat {{D_1}} + \widehat {DCI} + \widehat {{I_2}} = {180^0}\) (định lí tổng 3 góc trong tam giác) (2) \(\begin{array}{l} \Rightarrow 2\widehat {DCI} = \widehat {DCI} + \widehat {{I_2}}\\ \Rightarrow \widehat {DCI} = \widehat {{I_2}}\end{array}\) Suy ra tam giác DCI cân tại D \( \Rightarrow DI = DC\). Mà \(BI = DI(cmt) \Rightarrow BI = DC\) \( \Rightarrow AC = AD + DC = AB + BI\) (vì \(AD = AB,DC = BI\)) (đpcm) Bài 12. Cho \(\Delta ABC\) vuông tại A. Gọi M là trung điểm của BC. Phân giác \(\widehat {ABC}\) cắt AC tại I. Biết \(BI \bot AM\) tại H. a) Chứng minh \(IA = IM\). b) Tính các góc của \(\Delta BIC\). c) Trên tia đối của tia HB lấy điểm K sao cho \(HK = HB\). Chứng minh rằng \(\Delta AIB = \Delta KIC\). Phương pháp a) Chứng minh \(\Delta ABH = \Delta MBH\left( {g.c.g} \right) \Rightarrow AH = HM\) Chứng minh \(\Delta AHI = \Delta MHI\left( {c.g.c} \right) \Rightarrow IA = IM\) b) Chứng minh tam giác IBC cân tại I. Áp dụng định lí tổng ba góc trong tam giác vào tam giác ABC và IBC để tính các góc của tam giác IBC. c) Chứng minh BC // AK suy ra cặp góc so le trong bằng nhau. Chứng minh tam giác AIK cân tại I suy ra AI = IK Chứng minh \(\Delta AIB = \Delta KIC\) theo trường hợp cạnh – góc – cạnh. Lời giải
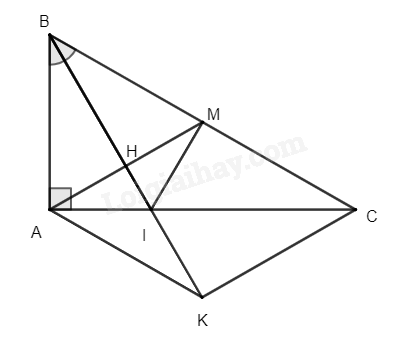
a) Xét tam giác ABH và tam giác MBH có: \(\widehat {ABH} = \widehat {MBH}\left( { = \frac{1}{2}\widehat {ABM}} \right)\) BH chung \(\widehat {AHB} = \widehat {MHB}\left( { = {{90}^0}} \right)\) \( \Rightarrow \Delta ABH = \Delta MBH\) (g.c.g) \( \Rightarrow AH = HM\) (hai cạnh tương ứng) Xét \(\Delta AHI\) và \(\Delta MHI\) có: AH = HM (cmt) \(\widehat {AHI} = \widehat {MHI}\left( { = {{90}^0}} \right)\) HI chung \( \Rightarrow \Delta AHI = \Delta MHI\) (c.g.c) \( \Rightarrow IA = IM\) (hai cạnh tương ứng) (đpcm) b) Xét \(\Delta ABI\) và \(\Delta MBI\) có: AB = BM (\(\Delta ABH = \Delta MBH\)) BI chung IA = IM (cmt) \( \Rightarrow \Delta ABI = \Delta MBI\) (c.c.c) \( \Rightarrow \widehat {BMI} = \widehat {BAI}\left( { = {{90}^0}} \right)\) Xét \(\Delta BMI\) và \(\Delta CMI\) có: BM = MC (M là trung điểm của BC) \(\widehat {BMI} = \widehat {IMC}\left( { = {{90}^0}} \right)\) IM chung \( \Rightarrow \Delta BMI = \Delta CMI\) (hai cạnh góc vuông) \( \Rightarrow BI = IC \Rightarrow \Delta BIC\) cân tại I \( \Rightarrow \widehat {IBM} = \widehat {MCI}\) Mà \(\widehat {IBM} = \frac{1}{2}\widehat {ABC} \Rightarrow \widehat {MCI} = \frac{1}{2}\widehat {ABC}\) Xét tam giác ABC có: \(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^0}\\{90^0} + 2\widehat {ACB} + \widehat {ACB} = {180^0}\\3\widehat {ACB} = {90^0}\\\widehat {ACB} = {30^0}\end{array}\) \( \Rightarrow \widehat {IBC} = \widehat {BCI} = {30^0}\) Xét tam giác BIC có: \(\begin{array}{l}\widehat {IBC} + \widehat {BCI} + \widehat {BIC} = {180^0}\\{30^0} + {30^0} + \widehat {BIC} = {180^0}\\\widehat {BIC} = {120^0}\end{array}\) Vậy số đo các góc của tam giác BIC là \(\widehat {BIC} = {120^0};\widehat {IBC} = \widehat {BCI} = {30^0}\) c) Xét tam giác ABH và tam giác AKH có: BH = HK (gt) \(\widehat {AHB} = \widehat {AHK}\left( { = {{90}^0}} \right)\) AH chung \( \Rightarrow \Delta ABH = \Delta AKH\) (c.g.c) \( \Rightarrow \widehat {ABH} = \widehat {AKH}\) (hai góc tương ứng) Mà \(\widehat {ABH} = \widehat {MBH}\left( { = \frac{1}{2}\widehat {ABM}} \right)\) \( \Rightarrow \widehat {AKH} = \widehat {HBM}\). Hai góc này ở vị trí so le trong nên BC // AK \( \Rightarrow \widehat {CAK} = \widehat {BCA}\) (hai góc so le trong) \( \Rightarrow \widehat {CAK} = \widehat {AKH}\) (vì \(\widehat {HBM} = \widehat {BCA}\)) \( \Rightarrow \Delta AIK\) cân tại I \( \Rightarrow AI = IK\) Xét \(\Delta AIB\) và \(\Delta KIC\) có: AI = IK (cmt) \(\widehat {AIB} = \widehat {KIC}\) (hai góc đối đỉnh) BI = IC (cmt) \( \Rightarrow \Delta AIB = \Delta KIC\) (c.g.c) (đpcm) Bài 13*. a) Tính GTNN của biểu thức \(A = 2 + 3\sqrt {{x^2} + 1} \); \(B = \left| {x - 1} \right| + \left| {x - 3} \right|\) b) Tính GTLN của biểu thức \(C = \frac{{5{x^2} + 12}}{{{x^2} + 2}}\); \(D = 4 - \left| {5x - 2} \right| - \left| {3y + 12} \right|\) Phương pháp a) * \(A = 2 + 3\sqrt {{x^2} + 1} \) Xét giá trị của \({x^2} + 1\) để tính giá trị của \(A = 2 + 3\sqrt {{x^2} + 1} \). * \(B = \left| {x - 1} \right| + \left| {x - 3} \right|\) Xét các điểm biểu diễn số thực x trên trục số. - Khi x nằm ngoài đoạn 1 và 3 - Khi x nằm trong đoạn 1 và 3 b) Biến đổi C, xuất phát từ \({x^2} \ge 0\,\forall x \in \mathbb{R}\) để tính giá trị lớn nhất của C. Biến đổi D thành \(D = 4 - \left( {\left| {5x - 2} \right| + \left| {3y + 12} \right|} \right)\), tính GTNN của \(\left| {5x - 2} \right| + \left| {3y + 12} \right|\). Lời giải * \(A = 2 + 3\sqrt {{x^2} + 1} \) Ta có: \(\begin{array}{l}{x^2} \ge 0\,\forall x \in \mathbb{R}\\{x^2} + 1 \ge 1\,\forall x \in \mathbb{R}\\\sqrt {{x^2} + 1} \ge 1\,\forall x \in \mathbb{R}\\2 + 3\sqrt {{x^2} + 1} \ge 2 + 3.1 = 5\,\forall x \in \mathbb{R}\end{array}\) Dấu “=” xảy ra khi và chỉ khi \({x^2} = 0\) hay \(x = 0\). Vậy giá trị nhỏ nhất của A là 5 khi x = 0. * \(B = \left| {x - 1} \right| + \left| {x - 3} \right|\) Xét các điểm biểu diễn số thực x trên trục số. Biểu thức đã cho đúng bằng tổng các khoảng cách từ x tới hai điểm 1 và 3 - Nếu x nằm ngoài đoạn giữa 1 và 3 thì tổng khoảng cách trên lớn hơn khoảng cách giữa 1 và 3 - Nếu x nằm trong đoạn giữa 1 và 3 thì tổng khoảng cách nói trên đúng bằng khoảng cách giữa 1 và 3 Vì vậy biểu thức B có giá trị nhỏ nhất là 2, đạt được khi \(1 \le x \le 3\) b) * \(C = \frac{{5{x^2} + 12}}{{{x^2} + 2}}\) Ta có: \(C = \frac{{5{x^2} + 12}}{{{x^2} + 2}} = \frac{{5\left( {{x^2} + 1} \right) + 7}}{{{x^2} + 2}} = 5 + \frac{7}{{{x^2} + 2}}\) Ta có: \(\begin{array}{l}{x^2} \ge 0\,\forall x \in \mathbb{R}\\{x^2} + 2 \ge 2\,\forall x \in \mathbb{R}\\\frac{1}{{{x^2} + 2}} \le \frac{1}{2}\forall x \in \mathbb{R}\\\frac{7}{{{x^2} + 2}} \le \frac{7}{2}\forall x \in \mathbb{R}\\5 + \frac{7}{{{x^2} + 2}} \le 5 + \frac{7}{2} = \frac{{17}}{2}\forall x \in \mathbb{R}\end{array}\) Dấu “=” xảy ra khi và chỉ khi \({x^2} = 0\) hay \(x = 0\). Vậy giá trị lớn nhất của A là \(\frac{{17}}{2}\) khi x = 0. * \(D = 4 - \left| {5x - 2} \right| - \left| {3y + 12} \right|\) Ta có: \(D = 4 - \left| {5x - 2} \right| - \left| {3y + 12} \right| = 4 - \left( {\left| {5x - 2} \right| + \left| {3y + 12} \right|} \right)\) đạt giá trị lớn nhất khi và chỉ khi \(\left| {5x - 2} \right| + \left| {3y + 12} \right|\) nhỏ nhất. Vì \(\left| {5x - 2} \right| \ge 0\,\forall x\) nên giá trị nhỏ nhất của \(\left| {5x - 2} \right| = 0\) khi \(x = \frac{2}{5}\); \(\left| {3y + 12} \right| \ge 0\,\forall y \in \mathbb{R}\) nên giá trị nhỏ nhất của \(\left| {3y + 12} \right| = 0\) khi \(y = - 4\) Vậy giá trị lớn nhất của D là \(D = 4 - \left( {0 + 0} \right) = 4\) khi \(x = \frac{2}{5}\), \(y = - 4\). Bài 14*. Cho \(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}};B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\). So sánh A và B. Nhân cả hai vế của A và B với 2023 để so sánh. Lời giải Ta có: \(\begin{array}{l}2023.A = \frac{{{{2023}^{2024}} + 2023}}{{{{2023}^{2024}} + 1}} = \frac{{\left( {{{2023}^{2024}} + 1} \right) + 2022}}{{{{2023}^{2024}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2024}} + 1}}\\2023.B = \frac{{{{2023}^{2023}} + 2023}}{{{{2023}^{2023}} + 1}} = \frac{{\left( {{{2023}^{2023}} + 1} \right) + 2022}}{{{{2023}^{2023}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\end{array}\) Vì \({2023^{2024}} + 1 > {2023^{2023}} + 1\) \(\begin{array}{l} \Rightarrow \frac{1}{{{{2023}^{2024}} + 1}} < \frac{1}{{{{2023}^{2023}} + 1}}\\ \Rightarrow \frac{{2022}}{{{{2023}^{2024}} + 1}} < \frac{{2022}}{{{{2023}^{2023}} + 1}}\\ \Rightarrow 1 + \frac{{2022}}{{{{2023}^{2024}} + 1}} < 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\\ \Rightarrow A < B\end{array}\) Vậy A < B
|