Đề thi học kì 1 Toán 7 - Đề số 12 - Kết nối tri thứcTổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài
I. Trắc nghiệm
Câu 1 :
Số đối của số \( - \frac{3}{5}\) là:
Câu 2 :
Căn bậc hai số học của 121 là:
Câu 3 :
Số nào là số vô tỉ trong các số sau:
Câu 4 :
Cho \(\left| x \right|\) = 16 thì giá trị của x là:
Câu 5 :
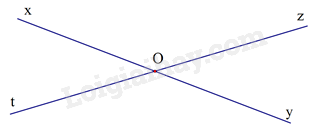
Cho hai đường thẳng xy và zt cắt nhau như hình vẽ, biết \(\widehat {xOz} = {140^0}\). Tính số đo \(\widehat {zOy}\):
Câu 6 :
Đường thẳng \(d\) là đường trung trực của đoạn thẳng \(AB\) khi và chỉ khi
Câu 9 :
Cho \(\widehat {xOy} = {120^0}\). Gọi Ot là tia phân giác của \(\widehat {xOy}\). Số đo\(\widehat {xOt}\) bằng:
Câu 11 :
Kết quả tìm hiểu về kết quả xếp loại học lực của các bạn học sinh Khối 7 được cho bởi bảng thống kê sau:
Xác định dữ liệu định tính trong bảng thống kê trên:
Câu 12 :
Cho đường thẳng c cắt hai đường thẳng a và b. Nhận định nào sau đây có thể chỉ ra hai đường thẳng a và b song song?
II. Tự luận
Câu 1 :
Thực hiện phép tính a) \(\frac{1}{3} - \frac{5}{4} + \frac{7}{6}\) b) \(\frac{{11}}{3}.\frac{2}{5} + \frac{{11}}{3}.\frac{8}{5} - \frac{{11}}{3}\)
Câu 2 :
Tìm x, biết \(\frac{1}{3} - \left| {\frac{3}{4} - x} \right| = \frac{1}{{12}}\)
Câu 3 :
Chia đều một thanh gỗ dài 6,323 m thành bốn đoạn thẳng bằng nhau. Tính độ dài mỗi đoạn gỗ (làm tròn đến hàng phần trăm)
Câu 5 :
Cho góc nhọn \(xOy\). Trên tia \(Ox\), lấy hai điểm \(A\) và \(C\). Trên tia \(Oy\) lấy hai điểm \(B\) và \(D\) sao cho: \(OA = OB,{\rm{ }}OC = OD\) (\(A\) nằm giữa \(O\) và \(C\); \(B\) nằm giữa \(O\) và \(D\)). a) Chứng minh: \(\Delta OAD = \Delta OBC\) b) So sánh hai góc: \(\;CAD\) và \(CBD\)
Câu 6 :
Làm tròn số 8 214 353 với độ chính xác d = 500
Câu 7 :
Nhân dịp 20 – 11 cửa hàng Juno giảm giá 5% cho tất cả các mặt hàng và nếu mua 2 sản phẩm cùng lúc sẽ chỉ tính tiền 1 sản phẩm cao giá nhất. Ngoài ra nếu có thẻ VIP thì sẽ được giảm thêm 10% trên giá đã giảm. Bạn Minh có thẻ VIP và mua 1 cái áo giá 325 000 đồng và 1 đôi giày giá 490 000 đồng. Hỏi Minh phải trả bao nhiêu tiền? Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Số đối của số \( - \frac{3}{5}\) là:
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về số đối. Lời giải chi tiết :
Số đối của số \( - \frac{3}{5}\) là \(\frac{3}{5}\).
Câu 2 :
Căn bậc hai số học của 121 là:
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của số a không âm là số x không âm sao cho \({x^2} = a\). Lời giải chi tiết :
Căn bậc hai số học của 121 là \(\sqrt {121} = 11\).
Câu 3 :
Số nào là số vô tỉ trong các số sau:
Đáp án : B Phương pháp giải :
Số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn. Lời giải chi tiết :
Ta có: \(0 = \frac{0}{1};3,15 = \frac{{63}}{{20}}\). Các số \(\frac{4}{5};0;3,15\) là số hữu tỉ nên không phải là số vô tỉ.
Câu 4 :
Cho \(\left| x \right|\) = 16 thì giá trị của x là:
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về dấu giá trị tuyệt đối. \(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x \ge 0\\ - x\,khi\,x < 0\end{array} \right.\) Lời giải chi tiết :
\(\left| x \right|\) = 16 thì x = 16 hoặc x = – 16.
Câu 5 :
Cho hai đường thẳng xy và zt cắt nhau như hình vẽ, biết \(\widehat {xOz} = {140^0}\). Tính số đo \(\widehat {zOy}\):
Đáp án : C Phương pháp giải :
Dựa vào kiến thức hai góc kề bù. Lời giải chi tiết :
Vì \(\widehat {xOz}\) và \(\widehat {zOy}\) là hai góc kề bù nên \(\widehat {xOz} + \widehat {zOy} = {180^0}\) suy ra \(\widehat {zOy} = {180^0} - \widehat {xOz} = {180^0} - {140^0} = {40^0}\).
Câu 6 :
Đường thẳng \(d\) là đường trung trực của đoạn thẳng \(AB\) khi và chỉ khi
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về đường trung trực. Lời giải chi tiết :
Đường thẳng \(d\) là đường trung trực của đoạn thẳng \(AB\) khi và chỉ khi \(d \bot AB\) tại \(I\)và \(IA = IB\).
Đáp án : A Phương pháp giải :
Tổng ba góc trong một tam giác bằng 1800. Tam giác đều có các góc bằng nhau và bằng 600. Lời giải chi tiết :
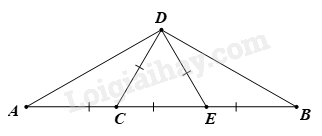
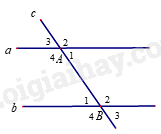
Xét tam giác CDE có CD = DE = EC nên tam giác CDE đều. Do đó \(\widehat {CDE} = \widehat {DEC} = \widehat {DCE} = {60^0}\). Góc DEB là góc ngoài đỉnh E của tam giác CDE nên \(\widehat {DEC} + \widehat {DEB} = {180^0}\) (hai góc kề bù). Suy ra \(\widehat {DEB} = {180^0} - {60^0} = {120^0}\). Tam giác DEB cân tại E (vì DE = EB). Xét tam giác DEB cân tại E có \(\widehat {DEB} = {120^0}\) nên \(\widehat {BDE} = \widehat B = \frac{{{{180}^0} - {{120}^0}}}{2} = {30^0}\).
Đáp án : D Phương pháp giải :
Kiểm tra điều kiện bằng nhau của hai tam giác. Lời giải chi tiết :
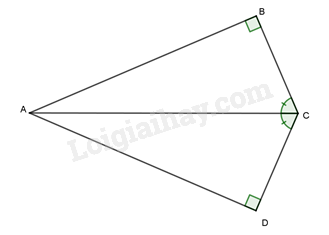
Hai tam giác vuông \(\Delta ABC\), \(\Delta ADC\) có cạnh huyền \(AC\) chung, góc nhọn \(\widehat {ACB} = \widehat {ACD}\) nên hai tam giác vuông \(\Delta ABC\), \(\Delta ADC\)bằng nhau theo trường hợp cạnh huyền – góc nhọn.
Câu 9 :
Cho \(\widehat {xOy} = {120^0}\). Gọi Ot là tia phân giác của \(\widehat {xOy}\). Số đo\(\widehat {xOt}\) bằng:
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về tia phân giác. Lời giải chi tiết :
Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}\widehat {xOy} = \frac{1}{2}{.120^0} = {60^0}\).
Đáp án : C Phương pháp giải :
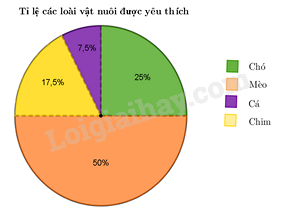
Quan sát biểu đồ để xác định. Lời giải chi tiết :
Quan sát biểu đồ, loài vật nuôi được yêu thích chiếm tỉ lệ cao nhất là mèo (chiếm 50%).
Câu 11 :
Kết quả tìm hiểu về kết quả xếp loại học lực của các bạn học sinh Khối 7 được cho bởi bảng thống kê sau:
Xác định dữ liệu định tính trong bảng thống kê trên:
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về dữ liệu định tính. Lời giải chi tiết :
Dữ liệu định tính là: 120; 285; 150; 25.
Câu 12 :
Cho đường thẳng c cắt hai đường thẳng a và b. Nhận định nào sau đây có thể chỉ ra hai đường thẳng a và b song song?
Đáp án : D Phương pháp giải :
Dựa vào dấu hiệu nhận biết hai đường thẳng song song. Lời giải chi tiết :
Góc A4 và góc B4 không phải hai góc so le trong nên A sai. Góc A4 và góc B2 không phải hai góc đồng vị nên B sai. Góc A2 và góc B2 không phải là hai góc trong cùng phía nên C sai. \(\widehat {{A_2}} = \widehat {{B_2}}\), góc A2 và góc B2 là hai góc đồng vị suy ra a // b nên D đúng.
II. Tự luận
Câu 1 :
Thực hiện phép tính a) \(\frac{1}{3} - \frac{5}{4} + \frac{7}{6}\) b) \(\frac{{11}}{3}.\frac{2}{5} + \frac{{11}}{3}.\frac{8}{5} - \frac{{11}}{3}\) Phương pháp giải :
Sử dụng các quy tắc thực hiện phép tính. Lời giải chi tiết :
a) \(\frac{1}{3} - \frac{5}{4} + \frac{7}{6}\) \( = \frac{4}{{12}} - \frac{{15}}{{12}} + \frac{{14}}{{12}} = \frac{3}{{12}} = \frac{1}{4}\) b) \(\frac{{11}}{3} \cdot \frac{2}{5} + \frac{{11}}{3} \cdot \frac{8}{5} - \frac{{11}}{3}\) \( = \frac{{11}}{3} \cdot \left( {\frac{2}{5} + \frac{8}{5} - 1} \right) = \frac{{11}}{3} \cdot \left( {2 - 1} \right) = \frac{{11}}{3}\)
Câu 2 :
Tìm x, biết \(\frac{1}{3} - \left| {\frac{3}{4} - x} \right| = \frac{1}{{12}}\) Phương pháp giải :
- Sử dụng quy tắc chuyển vế. - Chia hai trường hợp để bỏ dấu giá trị tuyệt đối. Lời giải chi tiết :
Ta có: \(\frac{1}{3} - \left| {\frac{3}{4} - x} \right| = \frac{1}{{12}}\) \(\begin{array}{l}\left| {\frac{3}{4} - x} \right| = \frac{1}{3} - \frac{1}{{12}}\\\left| {\frac{3}{4} - x} \right| = \frac{1}{4}\end{array}\) \(\left| {\frac{3}{4} - x} \right| = \frac{1}{4}\) thì \(\frac{3}{4} - x = \frac{1}{4}\) hoặc \(\frac{3}{4} - x = - \frac{1}{4}\) TH1. \(\frac{3}{4} - x = \frac{1}{4}\) \(\begin{array}{l}x = \frac{3}{4} - \frac{1}{4}\\x = \frac{1}{4}\end{array}\) TH2. \(\frac{3}{4} - x = - \frac{1}{4}\) \(\begin{array}{l}x = \frac{3}{4} + \frac{1}{4}\\x = 1\end{array}\) Vậy \(x \in \left\{ {\frac{1}{4};1} \right\}\).
Câu 3 :
Chia đều một thanh gỗ dài 6,323 m thành bốn đoạn thẳng bằng nhau. Tính độ dài mỗi đoạn gỗ (làm tròn đến hàng phần trăm) Phương pháp giải :
Sử dụng phép chia sau đó làm tròn kết quả đến hàng phần trăm. Lời giải chi tiết :
Độ dài mỗi đoạn gỗ là: \(6,323 \div 4 = 1,58075 \approx 1,58\)(m) Vậy độ dài mỗi đoạn gỗ là khoảng 1,58m. Phương pháp giải :
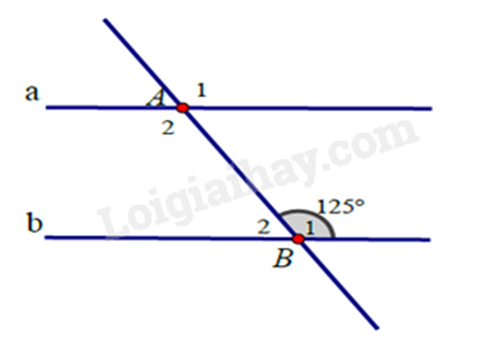
Dựa vào tính chất của hai đường thẳng song song. Lời giải chi tiết :
Vì a // b nên: \(\widehat {{A_1}} = \widehat {{B_1}} = {125^0}\) (hai góc đồng vị) Ta có: \(\widehat {{B_1}} + \widehat {{B_2}} = {180^0}\) (hai góc kề bù) Suy ra: \(\widehat {{B_2}} = {180^0} - \widehat {{B_1}} = {180^0} - {125^0} = {55^0}\).
Câu 5 :
Cho góc nhọn \(xOy\). Trên tia \(Ox\), lấy hai điểm \(A\) và \(C\). Trên tia \(Oy\) lấy hai điểm \(B\) và \(D\) sao cho: \(OA = OB,{\rm{ }}OC = OD\) (\(A\) nằm giữa \(O\) và \(C\); \(B\) nằm giữa \(O\) và \(D\)). a) Chứng minh: \(\Delta OAD = \Delta OBC\) b) So sánh hai góc: \(\;CAD\) và \(CBD\) Phương pháp giải :
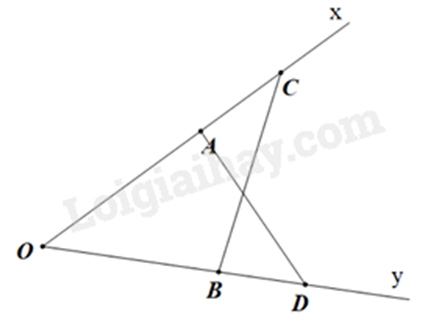
a) Chứng minh \(\Delta OAD = \;\Delta OBC\left( {c - g - c} \right)\) b) Dựa vào tính chất hai góc kề bù. Lời giải chi tiết :
a) Xét \(\Delta OAD\) và \(\Delta OBC\) có: \(OA{\rm{ }} = {\rm{ }}OB\) \(\widehat {COD}\) chung \(OD{\rm{ }} = {\rm{ }}OC\) (gt) Vậy \(\Delta OAD = \;\Delta OBC\left( {c - g - c} \right)\) b) Ta có: \(\Delta OAD = \;\Delta OBC\) (chứng minh trên) \(\; \Rightarrow \widehat {OAD} = \widehat {OBC}\)(hai góc tương ứng) Mà \(\widehat {OAD} + \widehat {CAD} = {180^o}\) (2 góc kề bù) \(\;\widehat {OBC} + \widehat {DBC} = {180^o}\)(2 góc kề bù) Vậy \(\widehat {CAD} = \widehat {DBC}\)
Câu 6 :
Làm tròn số 8 214 353 với độ chính xác d = 500 Phương pháp giải :
Dựa vào cách làm tròn số với độ chính xác cho trước. Lời giải chi tiết :
Do độ chính xác (d = 500) đến hàng trăm nên ta làm tròn số 8 214 353 đến hàng nghìn và ta có: \(8{\rm{ 214 353}} \approx {\rm{ 8 214 000}}\)
Câu 7 :
Nhân dịp 20 – 11 cửa hàng Juno giảm giá 5% cho tất cả các mặt hàng và nếu mua 2 sản phẩm cùng lúc sẽ chỉ tính tiền 1 sản phẩm cao giá nhất. Ngoài ra nếu có thẻ VIP thì sẽ được giảm thêm 10% trên giá đã giảm. Bạn Minh có thẻ VIP và mua 1 cái áo giá 325 000 đồng và 1 đôi giày giá 490 000 đồng. Hỏi Minh phải trả bao nhiêu tiền? Phương pháp giải :
Tính số tiền Minh phải trả sau khi giảm 5%. Tính số tiền Minh phải trả sau khi tính thẻ VIP. Lời giải chi tiết :
Vì Minh mua 1 cái áo giá 325 000 đồng và 1 đôi giày giá 490 000 đồng nên Minh sẽ phải trả tiền cho sản phẩm cao giá nhất đó là đôi giày giá 490 000 đồng. Số tiền Minh phải trả sau khi giảm giá 5% là: \(490\,000.\left( {100\% - 5\% } \right) = 465\;500\)(đồng). Số tiền Minh phải trả sau khi tính thẻ VIP là: \(465\;500.\left( {100\% - 10\% } \right) = 418\;950\)(đồng). Vậy số tiền Minh phải trả là 418 950 đồng. Phương pháp giải :
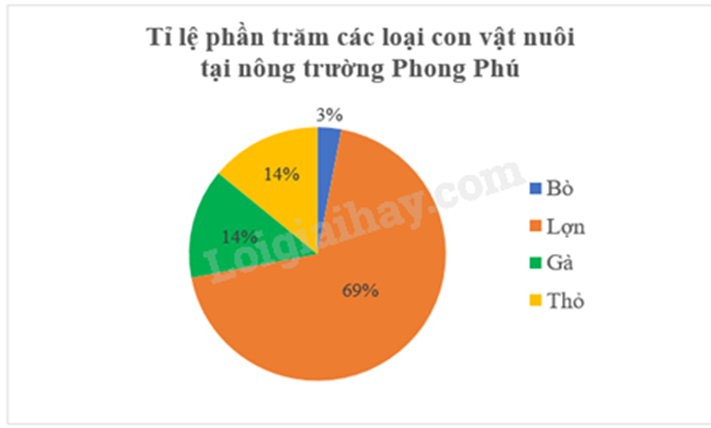
Dựa vào cách đọc biểu đồ. Lời giải chi tiết :
|
