Đề thi giữa kì 1 Toán 7 - Đề số 8 - Kết nối tri thứcTải về Phần trắc nghiệm (3 điểm) Câu 1. Chọn khẳng định đúng Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
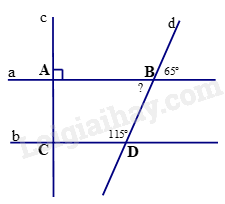
Đề bài Phần trắc nghiệm (3 điểm) Câu 1. Chọn khẳng định đúng A. \(\frac{3}{2} \in \mathbb{Q}.\) B. \(\frac{3}{2} \in \mathbb{Z}\). C. \(\frac{{ - 9}}{5} \notin \mathbb{Q}\). D. \( - 6 \in \mathbb{N}\). Câu 2. Số hữu tỉ dương là A. \(\frac{{ - 11}}{3}.\) B. \( - \frac{{12}}{5}.\) C. \(\frac{{ - 5}}{{ - 7}}.\) D. \(\frac{{15}}{{ - 13}}.\) Câu 3. Kết quả phép tính \(\frac{3}{7} + \frac{4}{7}.\frac{{ - 21}}{{35}}\) là A. \(\frac{3}{{35}}\). B. \(\frac{{ - 21}}{{35}}\). C. \(\frac{{ - 11}}{{35}}\). D. \(\frac{{11}}{{35}}\). Câu 4. Giá trị của \(x\) trong phép tính \(\frac{2}{5} - x = \frac{1}{3}\) bằng A. \(\frac{7}{{30}}.\) B. \(\frac{{ - 1}}{{15}}.\) C. \(\frac{{11}}{{15}}.\) D. \(\frac{1}{{15}}.\) Câu 5. Căn bậc hai số học của 81 là A. 9 và -9 B. \(\frac{{ - 1}}{{81}}.\) C. \( - 9.\) D. \(9.\) Câu 6. Khẳng định đúng là A. \(\left| { - 3,5} \right| = - 3,5\) B. \(\left| { - 3,5} \right| = 3,5.\) C. \(\left| { - 3,5} \right| = \pm 3,5\) D. \(\left| { - 3,5} \right| > 3,5.\) Câu 7. Số nào trong các số dưới đây viết được dưới dạng số thập phân hữu hạn A. \(\frac{{ - 7}}{{15}}\). B. \(\frac{{ - 7}}{{24}}\). C. \(\frac{{ - 5}}{{32}}\). D. \(\frac{{12}}{{45}}\). Câu 8. Giá trị của x trong đẳng thức - 0,6 = 1,4 là A. 2 hoặc -2. B. 0,6 hoặc -0,6. C. 2. D. -2. Câu 9. Giá trị của đẳng thức\(\sqrt {2 + 3 + 4 + 3 + 4} \) A. 16. B. -16. C. 4. D. -4. Câu 10. Cho ba đường thẳng phân biệt a, b, c biết \(a \bot c\)và \(c \bot b\). Kết luận nào đúng? A. \(a//b.\) B. \(c//b.\) C. \(c \bot b.\) D. \(c//a.\) Câu 11. Cho hình vẽ số đo góc “?” ở hình vẽ là A. 1300. B. 650. C. 900. D. 500.
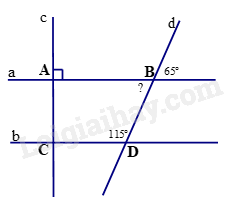
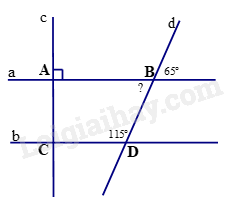
Câu 12. Cho hình vẽ số đo góc tại đỉnh C ở hình vẽ là A. 1150. B. 650. C. 900. D. 500.
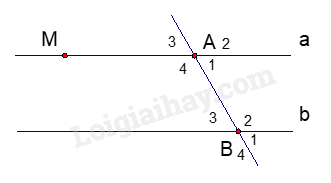
PHẦN II. TỰ LUẬN (7 điểm) Bài 1. ( 2,0 điểm) 1. So sánh: - 3,7634 và – 3,7654. 2. Thực hiện các phép tính sau a. \(\frac{2}{9} - {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\) b. \(17\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right) - 10\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right)\) Bài 2. ( 1,75 điểm) Tìm x, biết a. x + 4,5 = 7,5 b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\) c. |x| - 0,7 = 1,3 Bài 3. (2,25 điểm) Cho hình vẽ bên. Biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = {70^0}\). 1. Hãy viết tên các cặp so le trong và các cặp góc trong cùng phía. 2. Tính số đo của \(\widehat {{A_3}};\,\widehat {{B_3}}\) 3. Kẻ đường thẳng c vuông góc với đường thẳng a tại M. Chứng tỏ rằng: c \( \bot \) b
Bài 4. ( 1,0 điểm). So sánh A và B biết: \(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}}\) và \(B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\) -------- Hết -------- Lời giải Phần trắc nghiệm (3 điểm)
Câu 1. Chọn khẳng định đúng
Phương pháp Dựa vào khái niệm các tập hợp đã học. Lời giải \(\frac{3}{2}\) là số hữu tỉ nên \(\frac{3}{2} \in \mathbb{Q}.\) Đáp án A. Câu 2. Số hữu tỉ dương là
Phương pháp Dựa vào khái niệm số hữu tỉ. Lời giải \(\frac{{ - 5}}{{ - 7}} = \frac{5}{7}\) nên là số hữu tỉ dương. Đáp án C. Câu 3. Kết quả phép tính \(\frac{3}{7} + \frac{4}{7}.\frac{{ - 21}}{{35}}\) là
Phương pháp Dựa vào quy tắc tính với số hữu tỉ. Lời giải \(\begin{array}{l}\frac{3}{7} + \frac{4}{7}.\frac{{ - 21}}{{35}} = \frac{3}{7} + \frac{4}{7}.\frac{{ - 3}}{5} = \frac{3}{7} + \frac{{ - 12}}{{35}}\\ = \frac{{3.5 - 12}}{{35}} = \frac{3}{{35}}\end{array}\) Đáp án A. Câu 4. Giá trị của \(x\) trong phép tính \(\frac{2}{5} - x = \frac{1}{3}\) bằng
Phương pháp Sử dụng quy tắc trừ để tìm x. Lời giải \(\begin{array}{l}\frac{2}{5} - x = \frac{1}{3}\\x = \frac{2}{5} - \frac{1}{3}\\x = \frac{1}{{15}}\end{array}\). Vậy \(x = \frac{1}{{15}}\) Đáp án D. Câu 5. Căn bậc hai số học của 81 là
Phương pháp Dựa vào kiến thức về căn bậc hai số học. Lời giải Căn bậc hai số học của 81 là 9. Đáp án D. Câu 6. Khẳng định đúng là
Phương pháp Dựa vào kiến thức về giá trị tuyệt đối. Lời giải Vì -3,5 < 0 nên |-3,5| = - (-3,5) = 3,5. Đáp án B. Câu 7. Số nào trong các số dưới đây viết được dưới dạng số thập phân hữu hạn
Phương pháp Dựa vào kiến thức về số thập phân hữu hạn. Lời giải \(\frac{{ - 7}}{{15}} = - 0,4(6)\). \(\frac{{ - 7}}{{24}} = - 0,291(6)\). \(\frac{{ - 5}}{{32}} = - 0,15625\). \(\frac{{12}}{{45}} = 0,2(6)\). Đáp án C. Câu 8. Giá trị của x trong đẳng thức |x| - 0,6 = 1,4 là
Phương pháp Sử dụng quy tắc cộng và kiến thức về giá trị tuyệt đối để tìm x. Lời giải |x| - 0,6 = 1,4 |x| = 1,4 + 0,6 |x| = 2 Vậy x = 2 hoặc x = -2. Đáp án A. Câu 9. Giá trị của đẳng thức \(\sqrt {2 + 3 + 4 + 3 + 4} \)
Phương pháp Sử dụng quy tắc cộng và kiến thức về căn bậc hai để tính giá trị của đẳng thức. Lời giải \(\sqrt {2 + 3 + 4 + 3 + 4} = \sqrt {16} = 4\) Đáp án C. Câu 10. Cho ba đường thẳng phân biệt a, b, c biết \(a \bot c\)và \(c \bot b\). Kết luận nào đúng?
Phương pháp Dựa vào kiến thức về hai đường thẳng song song. Lời giải Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song. Vậy nếu biết \(a \bot c\)và \(c \bot b\) ta suy ra a // b. Đáp án A. Câu 11. Cho hình vẽ số đo góc “?” ở hình vẽ là
Phương pháp Dựa vào tính chất hai góc đối đỉnh. Lời giải Quan sát hình vẽ, ta thấy \(? = {65^0}\). Đáp án D. Câu 12. Cho hình vẽ số đo góc tại đỉnh C ở hình vẽ là
Phương pháp Tính số đo góc dBA, so sánh với góc BDC để xét AB // CD. Lời giải Ta có góc dBA kề bù với góc 650 nên \(\widehat {dBA} = {180^0} - {65^0} = {115^0} = \widehat {BDC}\). Mà góc dBA và góc BDC là hai góc đồng vị nên AB // CD. Do đó, \(\widehat C = \widehat A = {90^0}\)(hai góc đồng vị). Đáp án C.
Phần tự luận. Bài 1. ( 2,0 điểm) 1. So sánh: - 3,7634 và – 3,7654. 2. Thực hiện các phép tính sau
Phương pháp 1. So sánh 3,7634 với 3,7654, số nào lớn hơn thì thêm dấu trừ sẽ là số nhỏ hơn. 2. Sử dụng các quy tắc tính toán với số hữu tỉ để thực hiện phép tính. Lời giải 1. Ta có: 3,7634 < 3,7654 nên – 3,7634 > - 3,7654. 2. a. \(\frac{2}{9} - {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\) \(\begin{array}{l}\frac{2}{9} - \frac{1}{4} + \frac{5}{{18}}\\ = \left( {\frac{2}{9} + \frac{5}{{18}}} \right) - \frac{1}{4}\\ = \frac{1}{2} - \frac{1}{4}\\ = \frac{1}{4}\end{array}\) b. \(17\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right) - 10\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right)\) \(\begin{array}{l}\left( {17\frac{1}{3} - 10\frac{1}{3}} \right).\left( {\frac{{ - 5}}{7}} \right)\\ = 7.\left( {\frac{{ - 5}}{7}} \right)\\ = - 5\end{array}\) Bài 2. ( 1,75 điểm) Tìm x, biết
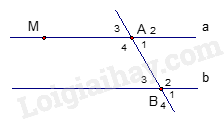
Phương pháp Dựa vào quy tắc tính để tìm x. Lời giải a. x + 4,5 = 7,5 x = 7,5 – 4,5 x = 3 Vậy x = 3. b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\) \(\begin{array}{l}\frac{2}{3}.x = \frac{4}{9} - \frac{1}{2}\\\frac{2}{3}x = - \frac{1}{{18}}\\x = - \frac{1}{{18}}:\frac{2}{3}\\x = - \frac{1}{{12}}\end{array}\) Vậy \(x = - \frac{1}{{12}}\). c. |x| - 0,7 = 1,3 |x| = 1,3 + 0,7 |x| = 2 x = -2 hoặc x = 2. Vậy x = -2 hoặc x = 2. Bài 3. (2,25 điểm) Cho hình vẽ bên. Biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = {70^0}\).
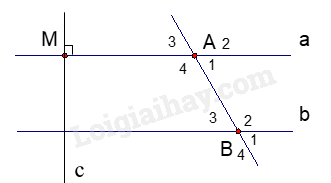
1. Hãy viết tên các cặp so le trong và các cặp góc trong cùng phía. 2. Tính số đo của \(\widehat {{A_3}};\,\widehat {{B_3}}\) 3. Kẻ đường thẳng c vuông góc với đường thẳng a tại M. Chứng tỏ rằng: c \( \bot \) b Phương pháp 1. Dựa vào tính chất của hai đường thẳng song song. 2. Dựa vào hai góc đối đỉnh và tính chất các góc của hai đường thẳng song song. 3. Dựa vào quan hệ giữa tính vuông góc và song song. Lời giải 1. Ta có a // b nên các cặp góc so le trong là: \(\widehat {{A_1}}\) và \(\widehat {{B_3}}\), \(\widehat {{A_4}}\) và \(\widehat {{B_2}}\). Các cặp góc trong cùng phía là \(\widehat {{A_1}}\) và \(\widehat {{B_2}}\), \(\widehat {{A_4}}\) và \(\widehat {{B_3}}\). 2. Ta có \(\widehat {{A_1}}\) và \(\;\widehat {{A_3}}\) là hai góc đối đỉnh nên \(\widehat {{A_1}}\) = \(\;\widehat {{A_3}}\) = 700. Vì a // b nên ta có \(\widehat {{A_3}} = \widehat {{B_3}}\) (hai góc đồng vị) nên \(\;\widehat {{A_3}}\)= \(\widehat {{B_3}}\) = 700. 3. Vì a \( \bot \) c và a // b nên b \( \bot \) c (mối quan hệ giữa tính vuông góc và song song. Bài 4. ( 1,0 điểm). So sánh A và B biết: \(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}}\) và \(B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\) Phương pháp Nhân cả A và B với 2023, đưa A và B về so sánh 2 phân số cùng tử, từ đó so sánh được A và B.
Lời giải Nhân A với 2023, ta được: \(2023A = \frac{{2023\left( {{{2023}^{2023}} + 1} \right)}}{{{{2023}^{2024}} + 1}} = \frac{{{{2023}^{2024}} + 2023}}{{{{2023}^{2024}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2024}} + 1}}\).
Nhân B với 2023, ta được: \(2023B = \frac{{2023\left( {{{2023}^{2022}} + 1} \right)}}{{{{2023}^{2023}} + 1}} = \frac{{{{2023}^{2023}} + 2023}}{{{{2023}^{2023}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\).
Ta có: \(\begin{array}{l}{2023^{2024}} > {2023^{2023}}\\{2023^{2024}} + 1 > {2023^{2023}} + 1\\\frac{1}{{{{2023}^{2024}} + 1}} < \frac{1}{{{{2023}^{2023}} + 1}}\\\frac{{2022}}{{{{2023}^{2024}} + 1}} < \frac{{2022}}{{{{2023}^{2023}} + 1}}\\1 + \frac{{2022}}{{{{2023}^{2024}} + 1}} < 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\\2023A < 2023B\\A < B\end{array}\) Vậy A < B.
|