Giải mục 1 trang 65, 66, 67, 68, 69 SGK Toán 12 tập 2 - Cánh diềuCho hình hộp ABCD.A’B’C’D’ (Hình 23). Giá của vectơ (overrightarrow {A'C'} ) và đường thẳng AC có vị trí tương đối như thế nào? Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Hoá - Sinh - Sử - Địa
Lựa chọn câu để xem lời giải nhanh hơn
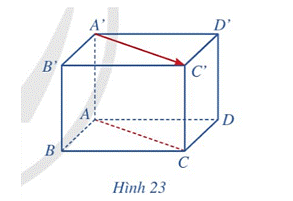
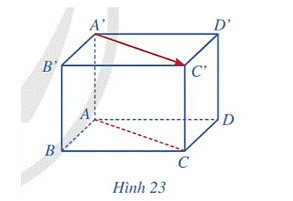
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 65 SGK Toán 12 Cánh diều Cho hình hộp ABCD.A’B’C’D’ (Hình 23). Giá của vectơ →A′C′ và đường thẳng AC có vị trí tương đối như thế nào?
Phương pháp giải: Sử dụng kiến thức về giá của vectơ trong không gian để trả lời: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ. Lời giải chi tiết: Giá của vectơ →A′C′ là đường thẳng A’C’. Mà AC//A’C’ (do ABCD.A’B’C’D’ là hình hộp) nên giá của vectơ →A′C′ song song đường thẳng AC. LT1 Trả lời câu hỏi Luyện tập 1 trang 65 SGK Toán 12 Cánh diều Trong Hình 23, vectơ →B′D′ có là vectơ chỉ phương của đường thẳng BD hay không? Vì sao?
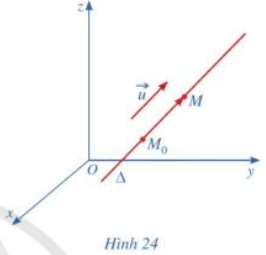
Phương pháp giải: Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để trả lời: Cho đường thẳng Δ và vectơ →u khác →0 . Vectơ →u được gọi là vectơ chỉ phương của đường thẳng Δ nếu giá của →u song song hoặc trùng với Δ. Lời giải chi tiết: Giá của vectơ →B′D′ là đường thẳng B’D’. Mà BD//B’D’ (do ABCD.A’B’C’D’ là hình hộp) nên vectơ →B′D′ là vectơ chỉ phương của đường thẳng BD. HĐ2 Trả lời câu hỏi Hoạt động 2 trang 66 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua điểm Mo(1;2;3) và có vectơ chỉ phương →u=(2;−3;5). Xét điểm M(x;y;z) nằm trên Δ (Hình 24).
a) Nêu nhận xét về phương của hai vectơ →u và →MoM. b) Có hay không số thực t sao cho →MoM=t→u? c) Hãy biểu diễn x, y, z qua t. d) Tọa độ (x; y; z) của điểm M (nằm trên Δ) có thỏa mãn hệ phương trình: {x=1+2ty=2−3tz=3+5t hay không? Phương pháp giải: + Sử dụng kiến thức về giá của vectơ trong không gian để trả lời: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ. + Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để trả lời: Cho đường thẳng Δ và vectơ →u khác →0 . Vectơ →u được gọi là vectơ chỉ phương của đường thẳng Δ nếu giá của →u song song hoặc trùng với Δ. Lời giải chi tiết: a) Hai vectơ →u và →MoM cùng phương với nhau. b) Vì hai vectơ →u và →MoM cùng phương với nhau nên tồn tại số thực t khác 0 sao cho →MoM=t→u. c) Ta có: →MoM=(x−1;y−2;z−3). Theo b ta có: →MoM=t→u nên {x−1=2ty−2=−3tz−3=5t. Do đó, {x=2t+1y=−3t+2z=5t+3. d) Vì M(x;y;z) và theo b ta có {x=2t+1y=−3t+2z=5t+3 nên tọa độ (x; y; z) của điểm M (nằm trên Δ) thỏa mãn hệ phương trình: {x=1+2ty=2−3tz=3+5t. LT2 Trả lời câu hỏi Luyện tập 2 trang 67 SGK Toán 12 Cánh diều Viết phương trình tham số của đường thẳng Δ, biết Δ đi qua điểm C(1;2;−4) và vuông góc với mặt phẳng (P): 3x−y+2z−1=0. Phương pháp giải: Sử dụng kiến thức về phương trình tham số của đường thẳng để viết phương trình tham số đường thẳng: Hệ phương trình {x=x0+aty=y0+btz=z0+ct, trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng Δ đi qua M0(x0;y0;z0) và có vectơ chỉ phương →u=(a;b;c). Lời giải chi tiết: Mặt phẳng (P) có một vectơ pháp tuyến là →n(3;−1;2). Vì đường thẳng Δ vuông góc với mặt phẳng (P) nên đường thẳng Δ nhận →n(3;−1;2) làm một vectơ chỉ phương. Lại có, Δ đi qua điểm C(1;2;−4) nên phương trình tham số của đường thẳng Δ là: {x=1+3ty=2−tz=−4+2t (t là tham số). HĐ3 Trả lời câu hỏi Hoạt động 3 trang 67 SGK Toán 12 Cánh diều Cho đường thẳng Δ có phương trình tham số: {x=2+3ty=4+7tz=5+8t (t là tham số). Tọa độ (x; y; z) của điểm M (nằm trên Δ) có thỏa mãn hệ phương trình x−23=y−47=z−58 hay không? Phương pháp giải: Sử dụng kiến thức về phương trình tham số của đường thẳng để trả lời câu hỏi: Hệ phương trình {x=x0+aty=y0+btz=z0+ct, trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng Δ đi qua M0(x0;y0;z0) và có vectơ chỉ phương →u=(a;b;c). Lời giải chi tiết: Vì M (x; y; z) nằm trên Δ nên {x=2+3ty=4+7tz=5+8t ⇒{t=x−23t=y−47t=z−58. Do đó, x−23=y−47=z−58. Do đó, điểm M(x; y; z) nằm trên Δ thỏa mãn hệ phương trình x−23=y−47=z−58. LT3 Trả lời câu hỏi Luyện tập 3 trang 68 SGK Toán 12 Cánh diều Viết phương trình chính tắc đường thẳng Δ, biết phương trình tham số của Δ là: {x=−1+2ty=3−5tz=6+9t (t là tham số). Phương pháp giải: Sử dụng kiến thức về phương trình chính tắc của đường thẳng để viết phương trình chính tắc của đường thẳng: Nếu abc≠0 thì hệ phương trình x−x0a=y−y0b=z−z0c được gọi là phương trình chính tắc của đường thẳng Δ đi qua M0(x0;y0;z0) và có vectơ chỉ phương →u=(a;b;c). Lời giải chi tiết: Đường thẳng Δ đi qua M(−1;3;6) và có vectơ chỉ phương →u=(2;−5;9) nên phương trình chính tắc của đường thẳng Δ là: x+12=y−3−5=z−69. HĐ4 Trả lời câu hỏi Hoạt động 4 trang 68 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;3) và B(3;5;9). a) Hãy chỉ ra một vectơ chỉ phương của đường thẳng AB. b) Viết phương trình tham số của đường thẳng AB. c) Viết phương trình chính tắc của đường thẳng AB. Phương pháp giải: + Sử dụng kiến thức về phương trình tham số của đường thẳng để viết phương trình tham số đường thẳng: Hệ phương trình {x=x0+aty=y0+btz=z0+ct, trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng Δ đi qua M0(x0;y0;z0) và có vectơ chỉ phương →u=(a;b;c). + Sử dụng kiến thức về phương trình chính tắc của đường thẳng để viết phương trình chính tắc của đường thẳng: Nếu abc≠0 thì hệ phương trình x−x0a=y−y0b=z−z0c được gọi là phương trình chính tắc của đường thẳng Δ đi qua M0(x0;y0;z0) và có vectơ chỉ phương →u=(a;b;c). Lời giải chi tiết: a) Một vectơ chỉ phương của đường thẳng AB là →AB=(2;3;6). b) Đường thẳng AB có một vectơ chỉ phương là →AB=(2;3;6). Mà đường thẳng AB đi qua điểm A(1;2;3) nên phương trình tham số của đường thẳng AB là: {x=1+2ty=2+3tz=3+6t (t là tham số). c) Phương trình chính tắc của đường thẳng AB là: x−12=y−23=z−36. LT4 Trả lời câu hỏi Luyện tập 4 trang 69 SGK Toán 12 Cánh diều Viết phương trình chính tắc của đường thẳng OM biết M(a; b; c) với abc≠0. Phương pháp giải: Sử dụng kiến thức về lập phương trình chính tắc của đường thẳng đi qua hai điểm để viết phương trình: Đường thẳng Δ đi qua hai điểm A(x0;y0;z0),B(x1;y1;z1) có phương trình chính tắc là: x−x0x1−x0=y−y0y1−y0=z−z0z1−z0 (với x0≠x1;y0≠y1;z0≠z1). Lời giải chi tiết: Phương trình chính tắc của đường thẳng OM là: x−0a=y−0b=z−0c⇔xa=yb=zc.
|