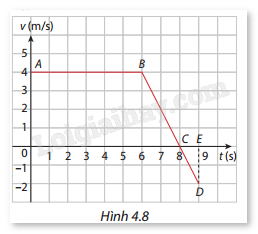
Giải bài tập 4.15 trang 20 SGK Toán 12 tập 2 - Cùng khám phá

Đề bài

Đường gấp khúc ABD trong Hình 4.8 là đồ thị vận tốc $v(t)$ của một vật (t = 0 là thời điểm vật bắt đầu chuyển động). Trong khoảng thời gian mà $v < 0$thì vật chuyển động ngược chiều với khoảng thời gian mà $v > 0$.

a) Viết công thức của hàm số $v(t)$ với $t \in [0;9]$.

b) Biết rằng quãng đường vật đi chuyển với vận tốc $v = v(t)$ từ thời điểm $t = a$ đến thời điểm $t = b$ là $s = \int_a^b | v(t)|{\mkern 1mu} dt$, tính quãng đường vật di chuyển được trong 9 giây kể từ khi vật bắt đầu chuyển động.

c) Tính tổng diện tích của hình thang $OABC$ và tam giác $CDE$ rồi so sánh với kết quả ở câu b.

Lời giải chi tiết

a)

- Đoạn $AB$: Ở đây, đồ thị có giá trị vận tốc không đổi là 4 m/s từ $t = 0$ đến $t = 6$, tức là:

$v(t) = 4\quad {\rm{,}}\quad t \in [0;6].$

- Đoạn $BC$ và $CD$: Đoạn này là một đường thẳng dốc xuống từ $t = 6$ đến $t = 8$, vận tốc giảm từ 4 m/s xuống -2 m/s. Phương trình đường thẳng có dạng:

$v(t) =  - 2t + 16\,\,\,\,\,\,{\rm{,}}\quad t \in [6;9].$

Vậy, công thức của hàm vận tốc $v(t)$ theo từng khoảng là:

$v(t) = \mathop \{ \nolimits_{ - 2t + 16\,\,\,\,\,\,khi\,\,6 < t \le 9}^{4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,0 \le t \le 6}$

b)

- Quãng đường được tính là tích phân của $|v(t)|$. Cần tính tích phân của các đoạn như sau:

Đoạn AB:

$\int_0^6 | v(t)|dt = \int_0^6 4 {\mkern 1mu} dt = 4 \times 6 = 24{\mkern 1mu} {\rm{m}}.$

Đoạn BC và CD:

$\int_6^9 | v(t)|dt = \int_6^9 {\left| { - 2t + 16} \right|} dt = \int_6^8 {\left( { - 2t + 16} \right)dt + } \int_8^9 {\left( {2t - 16} \right)dt}$

$\int_6^9 | v(t)|dt = \left. {( - {t^2} + 16t)} \right|_6^8 + \left. {({t^2} - 16t)} \right|_8^9 = 4 + 1 = 5m$

Tổng quãng đường vật di chuyển là:

$24 + 5 = 29{\mkern 1mu} {\rm{m}}.$

c)

Diện tích hình thang $OABC$:

Công thức diện tích hình thang: 

${S_{{\rm{ht}}}} = \frac{1}{2} \times (AB + OC) \times OA = \frac{1}{2} \times (6 + 8) \times 4 = 28{\mkern 1mu} .$

Diện tích tam giác $CDE$:

Công thức diện tích tam giác:

${S_{{\rm{tg}}}} = \frac{1}{2} \times CE \times ED = \frac{1}{2} \times 1 \times 2 = 1{\mkern 1mu}$

Tổng diện tích là:

${S_{{\rm{tong}}}} = 28 + 1 = 29$

Vậy kết quả ở câu c và câu b là giống nhau.