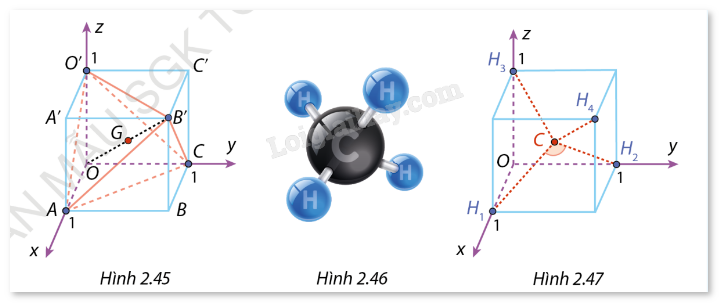
Giải bài tập 2.27 trang 82 SGK Toán 12 tập 1 - Cùng khám pháa) Trong không gian Oxyz, cho hình lập phương OABC.O’A’B’C’ với O(0;0;1), A(1;0;0), C(0;1;0) (Hình 2.45). G là trung điểm của đường chéo OB’ của hình lập phương. - Chứng minh rằng ACO’B’ là một tứ diện đều. - Tìm toạ độ các điểm B’ và G. Chứng minh rằng (overrightarrow {GA} + overrightarrow {GC} + overrightarrow {GO'} + overrightarrow {GB'} = vec 0). Điểm G được gọi là trọng tâm của tứ diện đều ACO’B’. Đề bài a) Trong không gian Oxyz, cho hình lập phương OABC.O’A’B’C’ với O(0;0;1), A(1;0;0), C(0;1;0) (Hình 2.45). G là trung điểm của đường chéo OB’ của hình lập phương. - Chứng minh rằng ACO’B’ là một tứ diện đều. - Tìm toạ độ các điểm B’ và G. Chứng minh rằng \(\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GO'} + \overrightarrow {GB'} = \vec 0\). Điểm G được gọi là trọng tâm của tứ diện đều ACO’B’. b) Methane là một chất khí và là nguồn nguyên liệu quan trọng trong đời sống cũng như trong công nghiệp. Công thức phân tử của methane là \({\rm{C}}{{\rm{H}}_4}\). Mỗi phân tử \({\rm{C}}{{\rm{H}}_4}\) được cấu tạo bởi bốn nguyên tử hydrogen H và một nguyên tử carbon \(C\). Trong cấu tạo của phân tử methane, bốn nguyên tử hydrogen tạo thành bốn đỉnh của một tứ diện đều và nguyên tử carbon ở vị trí trọng tâm của tứ diện đó (Hình 2.46). Người ta gọi góc liên kết là góc tạo bởi liên kết \({\rm{H}} - {\rm{C}} - {\rm{H}}\). Đó là góc có hai cạnh là hai đoạn thẳng nối nguyên tử C với hai trong bốn nguyên tử H , chẳng hạn như \(\widehat {{{\rm{H}}_1}{\rm{C}}{{\rm{H}}_2}}\) (nguồn: https://www.worldatlas.com/space/why-methane-can-be-a-sign-of-life-outside-of-earth.html). Để tính góc liên kết trong phân tử methane, người ta chọn hệ trục toạ độ mà các nguyên tử hydrogen lẩn lượt nằm ở các vị trí \({H_1}(1;0;0),{H_2}(0;1;0)\), \({H_3}(0;0;1),{H_4}(1;1;1)\)(Hình 2.47). Tính số đo của góc liên kết (làm tròn kết quả đến hàng đơn vị).
Phương pháp giải - Xem chi tiết a) - Sử dụng khái niệm của một tứ diện đều là các cạnh của nó bằng nhau. - Tìm toạ độ của các điểm và vectơ cần thiết, sau đó áp dụng biểu thức toạ độ của tổng các vectơ để chứng minh. b) - Sử dụng biểu thức đã được chứng minh ở câu a để tìm toạ độ của C. - Áp dụng công thức tính tích vô hướng của hai vectơ để tìm góc liên kết \(\cos \theta = \frac{{\overrightarrow {C{H_1}} \cdot \overrightarrow {C{H_2}} }}{{\left| {\overrightarrow {C{H_1}} } \right|.\left| {\overrightarrow {C{H_2}} } \right|}}.\) Lời giải chi tiết a) - Vì OABC.O’A’B’C’ là hình lập phương nên đường chéo của các mặt bên đều bằng nhau. Vậy ta có \(AC = AO' = AB' = CO' = CB' = O'B' = \sqrt 2 .\) - Ta thấy tất cả các cạnh của tứ diện ACO’B’ đều có độ dài bằng \(\sqrt 2 \). Do đó, tứ diện ACO’B’ là tứ diện đều. - Điểm B’ đối diện với điểm O qua hình lập phương, do đó tọa độ của B’ sẽ là: \(B'(1;1;1)\) - Trung điểm G của đường chéo OB’: \(G = \left( {\frac{{0 + 1}}{2};\frac{{0 + 1}}{2};\frac{{1 + 0}}{2}} \right) = \left( {\frac{1}{2};\frac{1}{2};\frac{1}{2}} \right)\) - Tính các vectơ: \(\overrightarrow {GA} = A - G = \left( {1 - \frac{1}{2};0 - \frac{1}{2};0 - \frac{1}{2}} \right) = \left( {\frac{1}{2}; - \frac{1}{2}; - \frac{1}{2}} \right)\)\(\overrightarrow {GC} = C - G = \left( {0 - \frac{1}{2};1 - \frac{1}{2};0 - \frac{1}{2}} \right) = \left( { - \frac{1}{2};\frac{1}{2}; - \frac{1}{2}} \right)\)\(\overrightarrow {GO'} = O' - G = \left( {0 - \frac{1}{2};0 - \frac{1}{2};1 - \frac{1}{2}} \right) = \left( { - \frac{1}{2}; - \frac{1}{2};\frac{1}{2}} \right)\)\(\overrightarrow {GB'} = B' - G = \left( {1 - \frac{1}{2};1 - \frac{1}{2};1 - \frac{1}{2}} \right) = \left( {\frac{1}{2};\frac{1}{2};\frac{1}{2}} \right)\) - Cộng các vectơ: \(\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GO'} + \overrightarrow {GB'} = \left( {\frac{1}{2} - \frac{1}{2} - \frac{1}{2} + \frac{1}{2}; - \frac{1}{2} + \frac{1}{2} - \frac{1}{2} + \frac{1}{2}; - \frac{1}{2} - \frac{1}{2} + \frac{1}{2} + \frac{1}{2}} \right) = \vec 0\) - Vậy \(\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GO'} + \overrightarrow {GB'} = \vec 0\). b) - Đặt toạ độ của C là \((x;y;z)\) - Vì C là trọng tâm của tứ diện đều \({H_1}{H_2}{H_3}{H_4}\), áp dụng biểu thức đã chứng minh ở câu a, ta có: \(\overrightarrow {C{H_1}} + \overrightarrow {C{H_2}} + \overrightarrow {C{H_3}} + \overrightarrow {C{H_4}} = \overrightarrow 0 \) - Thay các giá trị vào, ta được: \((1 - x) + (0 - x) + (0 - x) + (1 - x) = 0 \Rightarrow x = \frac{1}{2}\) \((0 - y) + (1 - y) + (0 - y) + (1 - y) = 0 \Rightarrow y = \frac{1}{2}\) \((0 - z) + (0 - z) + (1 - z) + (1 - z) = 0 \Rightarrow z = \frac{1}{2}\) - Vậy toạ độ của C là \(\left( {\frac{1}{2};\frac{1}{2};\frac{1}{2}} \right)\) - Toạ độ của vectơ \(\overrightarrow {C{H_1}} \)và \(\overrightarrow {C{H_2}} \) là: \(\overrightarrow {C{H_1}} = \left( {1 - \frac{1}{2};0 - \frac{1}{2};0 - \frac{1}{2}} \right) = \left( {\frac{1}{2}; - \frac{1}{2}; - \frac{1}{2}} \right)\) \(\overrightarrow {C{H_2}} = \left( {0 - \frac{1}{2};1 - \frac{1}{2};0 - \frac{1}{2}} \right) = \left( { - \frac{1}{2};\frac{1}{2}; - \frac{1}{2}} \right)\) - Tích vô hướng của \(\overrightarrow {C{H_1}} \)và \(\overrightarrow {C{H_2}} \): \(\overrightarrow {C{H_1}} \cdot \overrightarrow {C{H_2}} = \left( {\frac{1}{2} \times - \frac{1}{2}} \right) + \left( { - \frac{1}{2} \times \frac{1}{2}} \right) + \left( { - \frac{1}{2} \times - \frac{1}{2}} \right) = - \frac{1}{4}\) - Độ dài của \(\overrightarrow {C{H_1}} \)và \(\overrightarrow {C{H_2}} \) là: \(\left| {\overrightarrow {C{H_1}} } \right| = \left| {\overrightarrow {C{H_2}} } \right| = \frac{{\sqrt 3 }}{2}\) - Số đo của góc liên kết là: \(\cos \theta = \frac{{ - \frac{1}{4}}}{{\frac{{\sqrt 3 }}{2} \times \frac{{\sqrt 3 }}{2}}} = - \frac{1}{3}\) \(\theta = \arccos \left( { - \frac{1}{3}} \right) \approx {109.47^\circ }\) Vậy góc liên kết \({{\rm{H}}_1} - {\rm{C}} - {{\rm{H}}_2}\) xấp xỉ \({109^\circ }\).  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
